含三階色散項的非線性薛定諤方程的微擾對稱和近似解*

曹曉亮, 林 機

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

含三階色散項的非線性薛定諤方程的微擾對稱和近似解*

曹曉亮, 林 機

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

利用微擾對稱方法和經典李群方法的結合,研究了含三階群速度色散(GVD)的非線性薛定諤方程，得到了該方程關于高階微擾的近似解和約化常微分方程.并考慮了不同情況下的有限階微擾項或無窮階微擾的相似解和約化常微分方程.

三階群速度色散；微擾對稱方法；經典李群約化；相似解；約化方程

Theapproximatesymmetryperturbationandapproximate

0 引 言

非線性薛定諤方程(NLSE)

是一種應用廣泛的非線性方程,出現在量子力學、電磁學、非線性光學、等離子體理論、固體物理及玻色-愛因斯坦凝聚等眾多領域.對于NLSE的求解,學者們已經提出了很多方法，如逆散射方法(IST)[1]、Darboux變換[2]、Backlund變換[3]、Hirota方法[4]、Painlevé展開方法[5]等.

在非線性光學中，NLSE是描述光波在弱非線性色散介質中傳播的方程，但NLSE是一個理想化的方程，它忽略了高階的色散效應和自陡、沖擊效應及自頻移效應等.當我們必須考慮這些效應的時候，方程(1)的可積性就被破壞了.但當外加效應較弱時，微擾的方法可以有效地處理這類問題.目前的微擾方法有：反散射微擾方法[6]、修正微擾守恒律方法[7-10]、直接微擾法[11-12]等.反散射微擾方法比較復雜且不能很好地處理非零邊界的問題，同時這些方法不能得到高階的微擾項.

最近，焦小玉等提出了一種微擾對稱方法[13-15]，并對微擾的Boussinesq方程和Kdv-Burgers方程進行了研究.這種方法將微擾和對稱相結合，思路簡單，操作方便，而且把求解高階微擾的問題簡化為求解相應的約化后的常微分方程的問題.

筆者采用微擾對稱方法研究三階GVD微擾的非線性薛定諤方程(PNLSE)[16]

式(2)中：u是關于x,t的復變函數;參量ε是同三階GVD相關的小參量.在實際情況下，二階GVD的影響是主要的，但是當入射是脈寬T0lt;1 ps的超短脈沖時,即使二階GVD不等于零，也需要考慮三階GVD的影響.方程(2)是用來描述在考慮三階GVD的情況下，超短光脈沖在單模光纖中的傳播.這個方程不具有Painlevé性質[17].

1 微擾對稱

將u按照ε級數展開，即

式(3)中un是關于x,t的函數.將式(3)代入方程(2),令各階ε的系數等于0，得

…

其中u-1=0.

雖然式(4)為標準的非線性薛定諤方程，它是一個完全可積的方程，有很多的孤子解，但是式(5)是關于u1的變系數的線性偏微分方程，直接求解有較大的困難.若u1不能求解，就難以求得u2,u3,…,un.對稱約化方法是研究非線性偏微分方程(可積和不可積)行之有效的方法.因此，筆者利用對稱約化方法研究方程(4)～(8)的解析解.為了得到這組方程的解析解，筆者將un寫成

式(9)中，pn,qn是關于x,t的實函數.

將方程(9)代入方程(4)～(8),并分離實虛部，得：

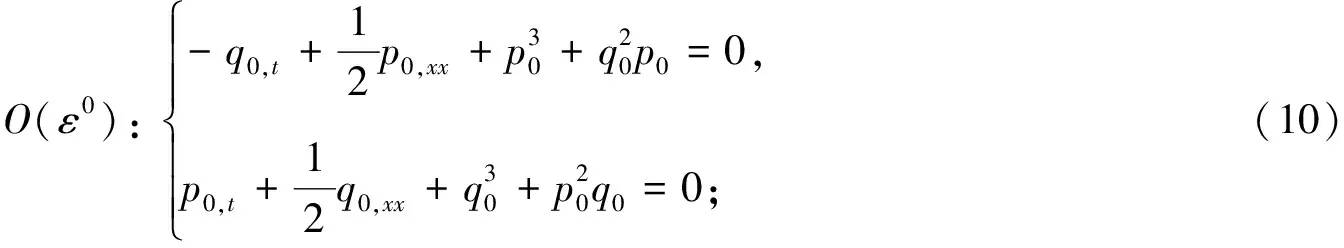
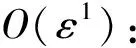
(11)

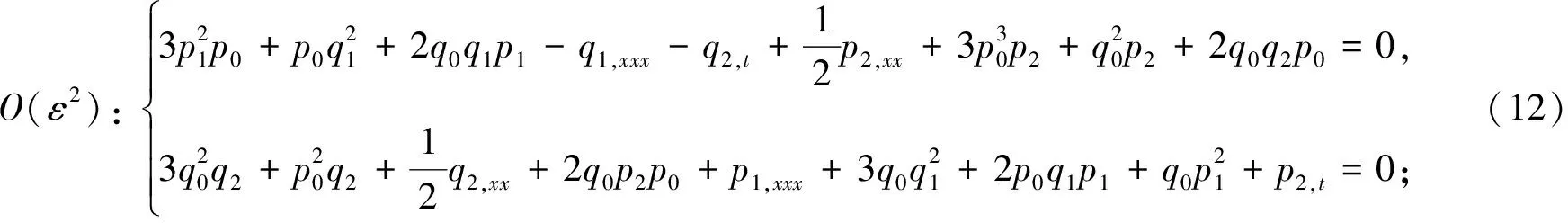
(13)

…

因此，q-1=0,p-1=0.

為了對方程(14)進行對稱約化，筆者寫出李點對稱的向量場

式(15)中:X,T,PN,Qn是x,t,pj,qj(j=0,1,…,n)的函數.根據李點對稱的定義,方程組(14)在pn→pn+εσn,qn→qn+εδn(n=0,1,…,∞)的無窮小變換下不變.對稱方程為

式(16)中：n=0,1,…,∞;σ-1=0;δ-1=0.

當n取無窮大時，方程組(16)包含無窮多個方程，且方程中X,T,Pn,Qn是無窮多個變量的函數，幾乎不能求解.為了簡化問題，可以先求解有限個方程的情況.當n=0，1，2時，{X,T,P0,P1,P2,Q0,Q1,Q2}是{x,t,p0,p1,p2,q0,q1,q2}的函數.把式(15)代入方程組(16)中，利用方程組(10)～(12)消去{P0,t,P1,t,P2,t,Q0,t,Q1,t,Q2,t},得到關于{X,T,P0,P1,P2,Q0,Q1,Q2}的待定方程，借助Maple軟件,解得

在這里，d1,d2,d3,C0,C1,C2是任意常數.

選擇n=0，1，2，3時，{X,T,P0,P1,P2,P3,Q0,Q1,Q2,Q3}是{x,t,p0,p1,p2,p3,q0,q1,q2,q3}的函數，類似于n=01，2時的計算過程，得

這里d1～d3,C0～C3是任意常數.

以上的過程重復幾次，即可得到X,T,Pn,Qn的通式

2 經典李群約化

2.1情況1d1≠0

通過求解特征方程

得到方程(4)～(8)的相似解：

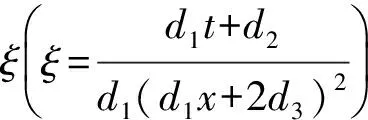
把式(21)～式(23)代入方程(4)～(6) 得到約化方程：

由于d1≠0時相似解和約化方程比較復雜，我們未能得到任意階微擾的約化方程，只能得到有限階微擾項的相似解和約化方程.

2.2情況2d1=0

通過求解特征方程(20),得到相似解:

(29)

…

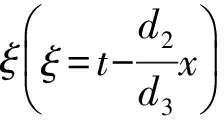
筆者把相似解方程(35)代入方程(4)～(8)得到相應各階的約化方程為：

…

方程(38)是各階微擾的約化方程的遞推關系.通過逐次求解各階常微分方程，可以得到方程(2)的各階微擾.

3 結 論

[1]Manakov S V.On the theory of two-dimensional stationary[J].Sov Phys JETP,1974,38:248-253.

[2]Chen H H.General Derivation of B?cklund Transformations from Inverse Scattering Problems[J].Phys Rev Lett,1974,33(15):925-928.

[3]Wahlquist H D,Estabrook F B.B?cklund Transformation for Solutions of the Korteweg-de Vries Equation[J].Phys Rev Lett,1973,31(23):1386-1390.

[4]Hirota R.Exact Solution of the Korteweg-de Vries Equation for Multiple Collisions of Solitons[J].Phys Rev Lett,1971,27(18):1192-1194.

[5]Weiss J,Tabor M,Carneval G.The Painlevé property for partial differential equations[J].J Math Phys,1983,24:522-526.

[6]Kaup D J.A Perturbation Expansion for the Zakharov-Shabat Inverse Scattering Transform[J].SIAM (Soc Ind Appl Math) J Appl Math,1976,31(1):121-133.

[7]Kodama Y，Yuji.On integrable systems with higher order corrections[J].Phys Lett A,1985,107(6):245-249.

[8]Kodama Y,Yuji.Normal forms for weakly dispersive wave equations[J].Phys Lett A,1985,112(5):193-196.

[9]Kodama Y,Yuji.Nearly integrable systems[J].Physica D,1985,16(1):14-26.

[10]Kodama Y,Yuji.On solitary-wave interaction[J].Phys Lett A,1987,123(6):276-282.

[11]Lou Senyue.A Direct Perturbation Method:Nonlinear Schr?dinger Equation with Loss[J].Chin Phys Lett,1999,16(9):659-661.

[12]Cheng Xueping,Lin Ji,Ye Lijun.Asymptotical solutions of coupled nonlinear Schr?dinger equations with perturbations[J].Chin Phys,2007,16(9):2503-2509.

[13]Jiao Xiaoyu,Yao Ruoxiao,Lou Senyue.Approximate similarity reduction for singularly perturbed Boussinesq equation via symmetry perturbation and direct method[J].J Math Phys,2008,49(9):093505.

[14]Jiao Xiaoyu,Yao Ruoxia,Zhang Shunli,et al.Approximate symmetry reductions to the Kdv-Burgers equation[J/OL].[2008-01-06].http://arxiv.org/abs/0801.0856.

[15]Jia Man,Wang Jianyong,Lou Senyue.Approximate Symmetry Reduction to the Perturbed One-Dimensional Nonlinear Schr?dinger Equation[J].Chin Phys Lett,2009,26(2):020201.

[16]Agramal G P.Nonlinear Fiber Optics amp; Application of Nonlinear Fiber Optics[M]. 賈東方，余震虹，談斌，等,譯.北京:電子工業出版社, 2002:32.

[17]Mihalache D,Truta N,Crasovan L C.Painlevé analysis and bright solitary waves of the higher-order nonlinear Schr?dinger equation containing third-order dispersion and self-steepening term[J].Phys Rev E,1997,56(1):1064-1070.

(責任編輯 杜利民)

solutionsofthenonlinearSchr?dingerequationswiththetermofthirdordergroupvelocitydispersion

CAO Xiaoliang, LIN Ji

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

The approximate symmetry perturbation method combining with classical Lie group method was applied to study nonlinear Schr?dinger equation with third order group velocity dispersion (GVD). Similarity solutions and reduction ordinary differential equation were obtained for the corresponding high order modifications. Similarity solutions and reduction equations corresponding finite and infinite order modifications were als considered under different conditions.

the third order group velocity dispersion; approximate symmetry perturbation; classical Lie group method; similarity solution; reduction equation

1001-5051(2010)01-0056-07

2009-10-28

國家自然科學基金資助項目(10875106)

曹曉亮(1984-)，男，浙江湖州人，碩士研究生.研究方向：非線性物理.

O41

A