索拱組合結構的動力建模及其內共振分析

呂建根 ，趙躍宇，王榮輝

(1. 華南理工大學 土木與交通學院，廣東 廣州，510641；2. 仲愷農業工程學院 城市建設學院，廣東 廣州，510225；3. 湖南大學 土木工程學院，湖南 長沙，410082)

1 索拱組合結構的動力學方程

索拱組合結構模型如圖1所示。為了建模方便，將索的運動在坐標系xOy中描述，拱的運動在中描述。圖1中：θc和θg分別為索和拱的水平傾角；lc和lg分別為索和拱在相應坐標系中的跨度；dc和dg分別為索的初始垂度和拱的矢高。

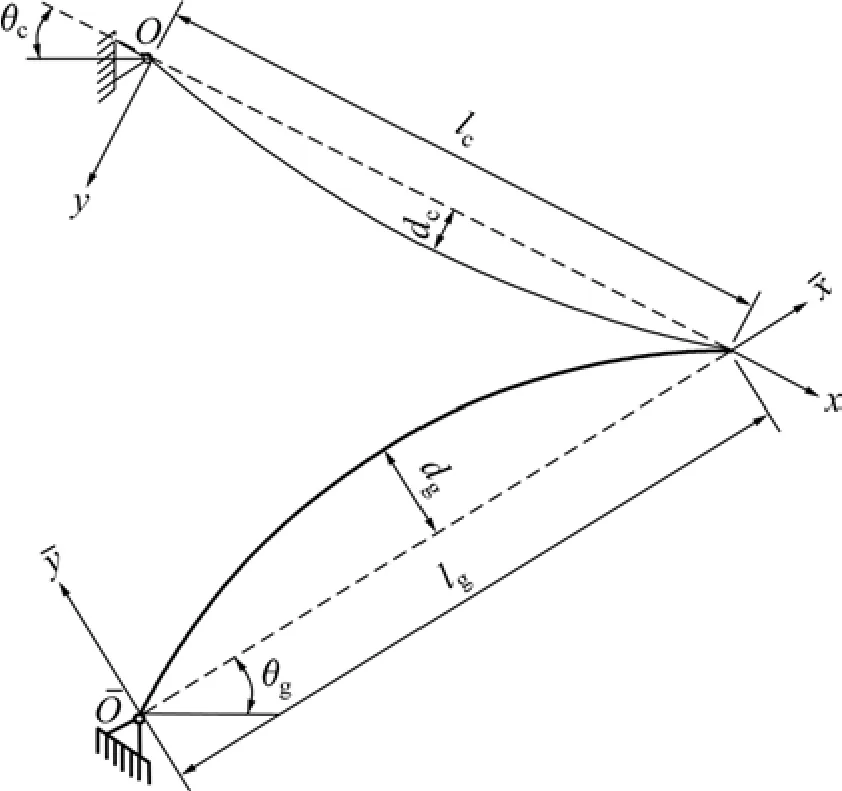
圖1 索拱組合結構相互作用分析模型Fig.1 Mechanical model of cable-stayed arch

對于如圖1所示坐標系，索和拱在右端端點鉸接。根據位移協調條件，其連接關系式如下：

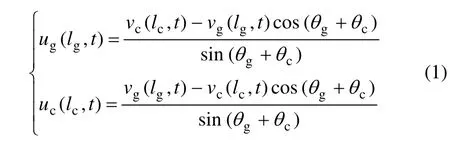
式中：ug和uc分別為拱和索在長度方向的縱向位移；vg和vc分別為拱和索的橫向振動位移。

根據索的三維非線性運動控制方程[12]，通過化簡整理可得到拉索平面運動學方程：

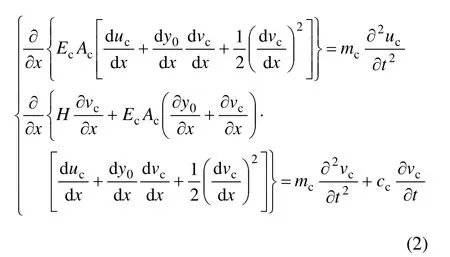
式中：EcAc為索的抗壓剛度；mc為索的單位長度質量；H為索的初始張力；y0為斜拉索的初始線性方程，為x的函數；cc為彈性索的結構阻尼系數。

由于彈性索縱向變形遠小于其橫向變形，而橫向振動頻率與縱向振動頻率相差很大，因此，縱向慣性力可以忽略。將式(2)中第 1式兩邊同時對 xc在區間[0, lc]內積分，結合式(1)，可以得到彈性索在考慮縱向位移后的橫向運動微分方程：

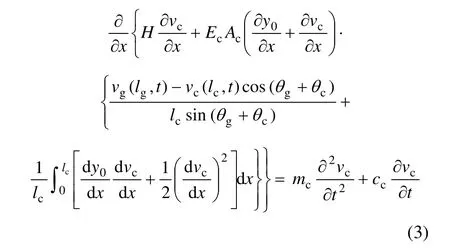
在大跨度纜索吊裝施工過程中，懸臂拱在如圖1所示的局部坐標系下，懸臂拱的矢跨比 dg/lg通常都小于 1/10，可以將吊裝過程中的懸臂拱當成淺拱考慮[13]，得到考慮右端點縱向位移后拱橫向運動微分方程[14?15]：

我國會計法律法規對會計人員的職業行為和專業素質提出了更高要求，國家關于會計工作的相關法律法規，職業道德要求是每一名會計人員在日常工作中必須遵守的規范。通過對會計人員繼續教育培訓，確保會計隊伍全面掌握最新的法律法規，以及對會計人員工作行為的要求。在全新的歷史時期，我們應該充分認識到會計人員繼續教育也是國家法律法規管理工作提出的新要求，是加強會計隊伍有效管理的重要組成部分，更是加強會計人才隊伍建設的重要內容。開展會計人員繼續教育培訓的目的是為了提高會計人員的政治素養、業務能力、職業道德水平，使其及時更新專業知識，補充和拓展專業素質。

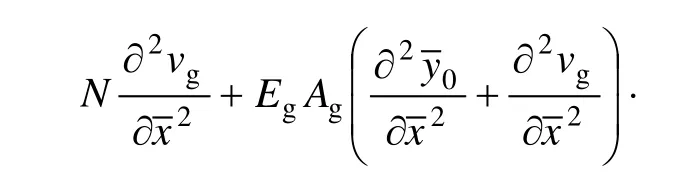
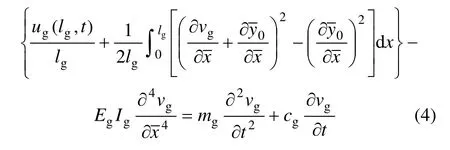
將式(1)中的第1式代入式(4)，得到：

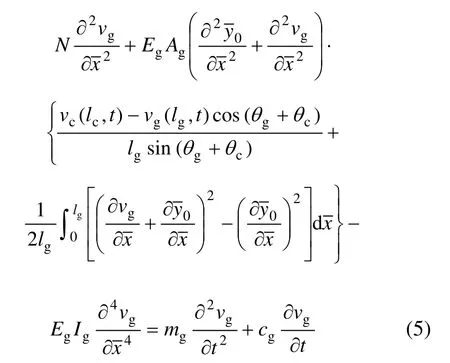
式中：N為拱的初始軸向力；EgIg為拱的面內抗彎剛度；為拱在局部坐標系中的初始拱軸線方程；cg為彈性拱的結構阻尼系數；mg為拱的單位長度質量；EgAg為拱的抗壓剛度。

聯立式(3)和式(5)，即得到索拱組合結構耦合橫向運動方程。

2 索拱組合結構的內共振分析

在拱橋施工過程中的索拱組合結構中，扣索的自振頻率通常比彈性拱的自振頻率低很多，索拱之間相互激勵而產生的內共振往往是扣索的高階與彈性拱的低階振動，因而，在對索拱組合結構相互作用的內共振分析過程中，必須包括索拱的高階模態。下面對索拱耦合運動方程(3)和式(5)進行 Galerkin高階模態截斷，設

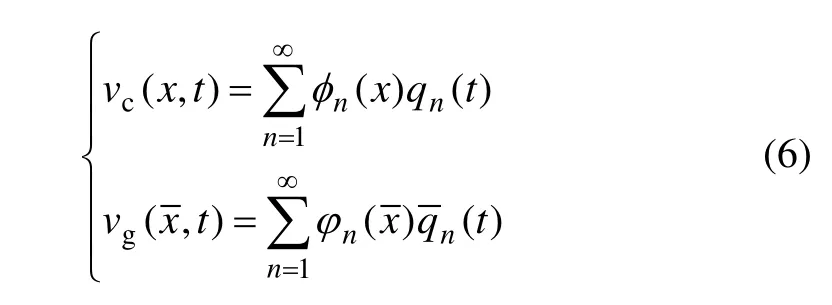
其中： φn(x)和?n(x)分別為索和拱的振型函數；qn(t)和( t )分別為索和拱的振動函數。

將式(6)代入式(3)和式(5)，在式(3)兩邊乘以 φi(x)并在[0, lc]內積分，在式(5)式兩邊乘以?i()并在[0, lg]內積分，利用振型函數的正交性，得到索拱組合結構

多階離散動力學方程：

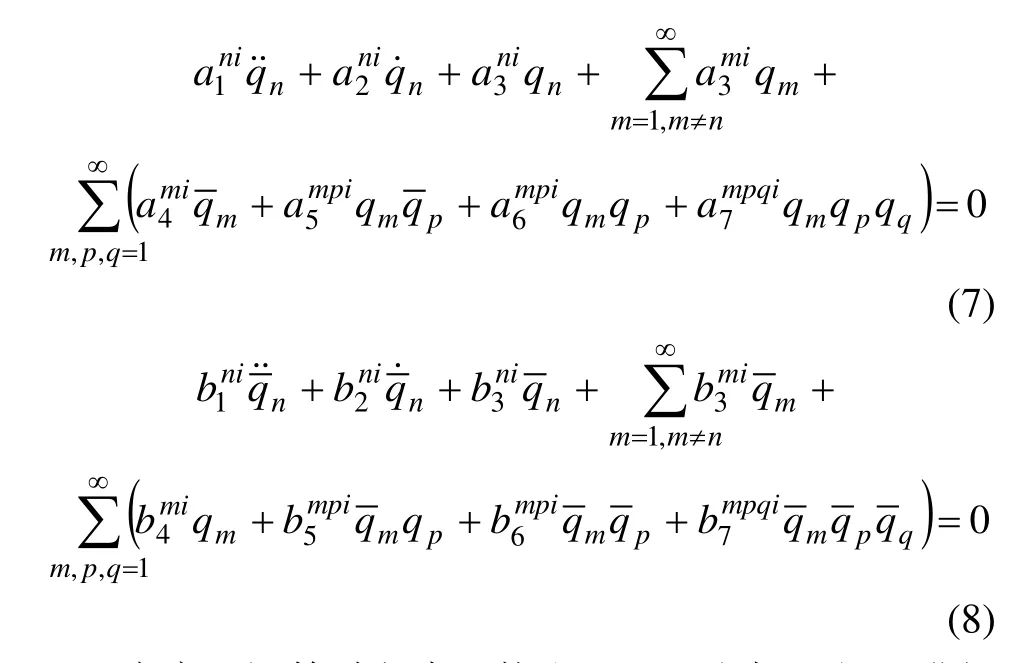
在實際運算過程中，均取 i=n。對式(7)和(8)進行化簡，對式(7)兩邊同除以，對式(8)兩邊同除以，引入任意小的正數ε，并定義系數(見文獻[16])，代入式(7)和式(8)，可得到：

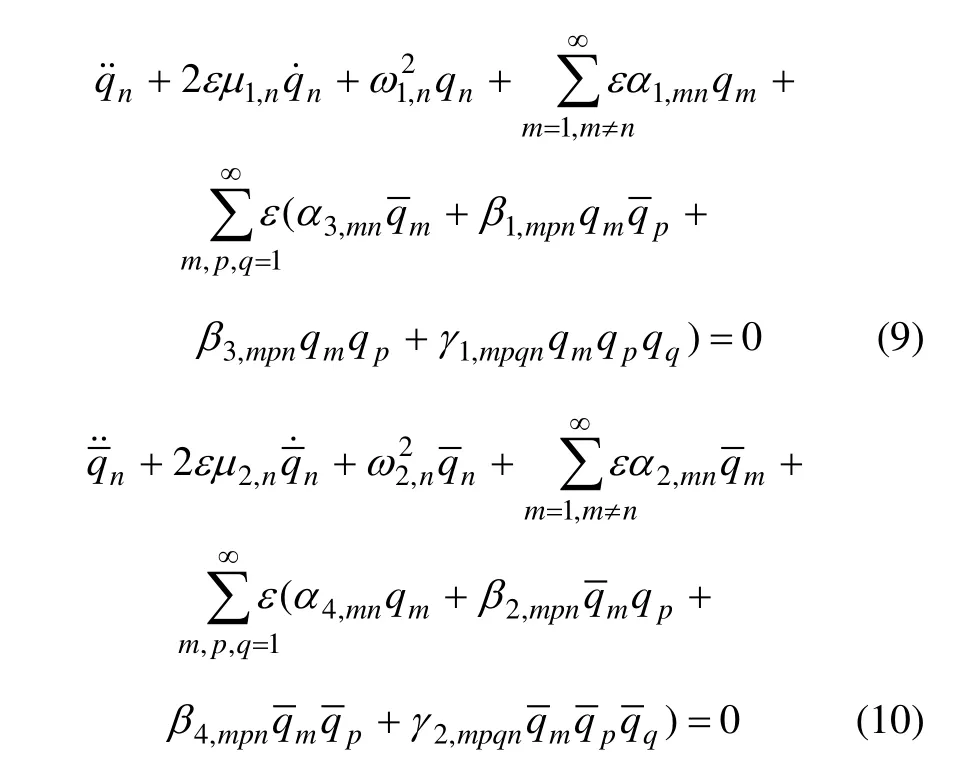
采用多尺度攝動方法尋找qn和的一致漸近解，引入快變時間尺度T0=t和慢變時間尺度T1=ε t ，設解的形式如下：

將式(10)代入式(9)，可以得到索拱組合結構的一階近似方程：

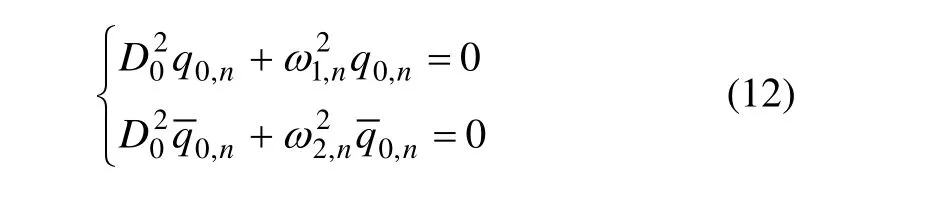
式(11)復數形式的解為：

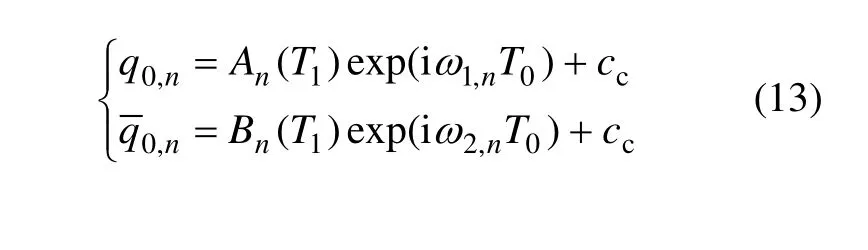
將式(12)代入二階近似方程并整理得：

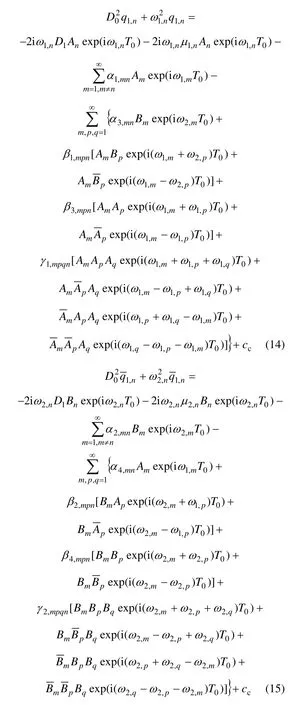
式中：cc為 c相應的共軛項。從式(13)可以看出：當時，索和拱之間存在相互作用的內共振；同時，由于索和拱的自振頻率相差很大，若進行低階模態截斷，則只有索和拱自身模態之間的亞諧波和超諧波內共振產生，索拱之間不會相互作用而產生內共振，但是，若考慮索和拱的高階模態，則在索的高階模態和拱的低階模態之間將產生內共振。因此，對索和拱組合結構體系進行相互作用的非線性動力學分析時，應進行高階模態截斷，而且隨著模態的增加，內共振模式將大大增加。

3 索拱組合結構內共振的數值模擬

為了證實所建立的索拱組合結構非線性動力學模型及分析理論的正確性，以某鋼管混凝土拱橋纜索吊裝施工過程中第1節段結構體系為數值研究對象，忽略扣塔振動的影響，建立索拱組合結構的非線性動力學力學模型(參考圖1)，索和拱的結構參數分別見表1和表 2。求解方程系數，可知該結構體系為弱非線性動力學問題。

表1 索的結構參數Table 1 Structural parameters of cable

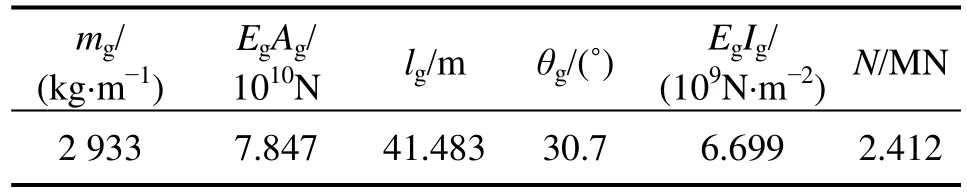
表2 拱的結構參數Table 2 Structural parameters of the arch

給定索和拱的初始位移均為0.01 m，繪制索和拱的100 s時間歷程曲線，見圖2。從圖2可以看出：在非共振情形下，索和拱之間的振動相互耦合非常弱，索和拱的振幅都約等于初始位移，因此，若索拱組合結構的結構設計參數都處在結構的非共振區域以內，則索和拱的動力學特性可以單獨進行分析，可不考慮振動時索和拱之間的相互影響。

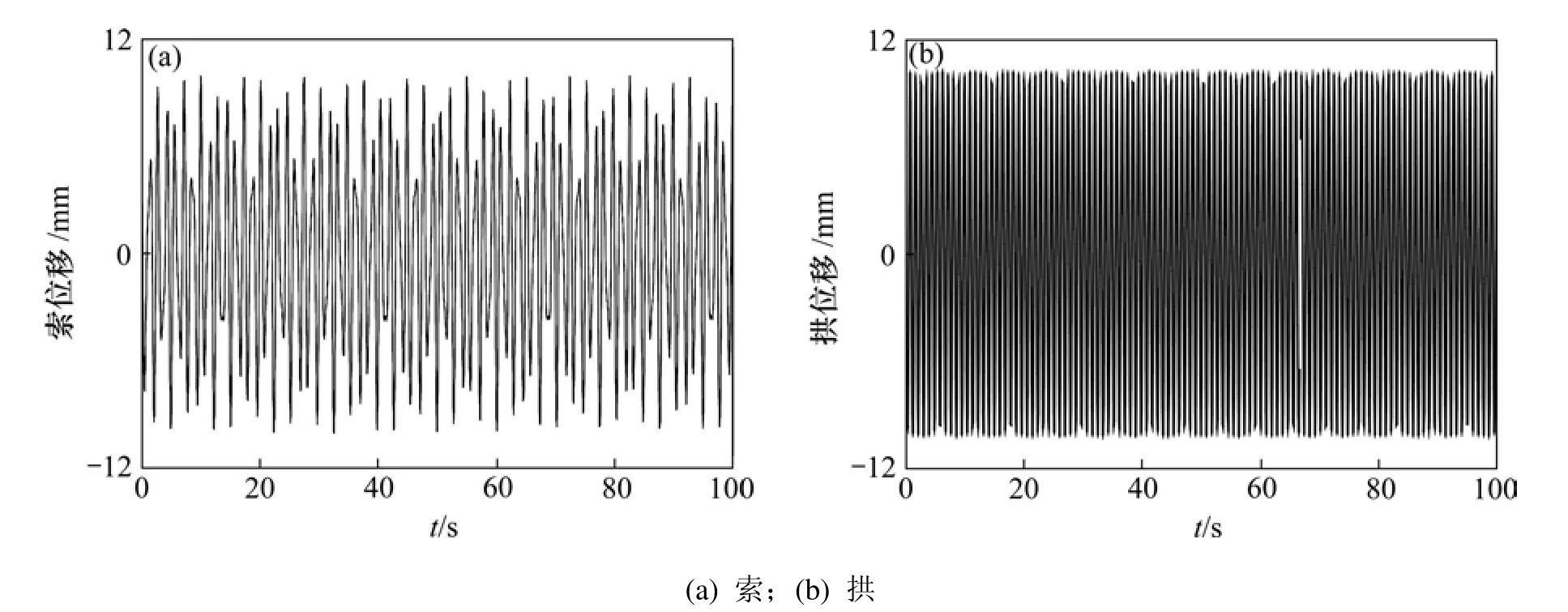
圖2 索拱組合結構非內共振情形下的時間歷程Fig.2 Time history of cable-stayed arch structure under non-resonance state

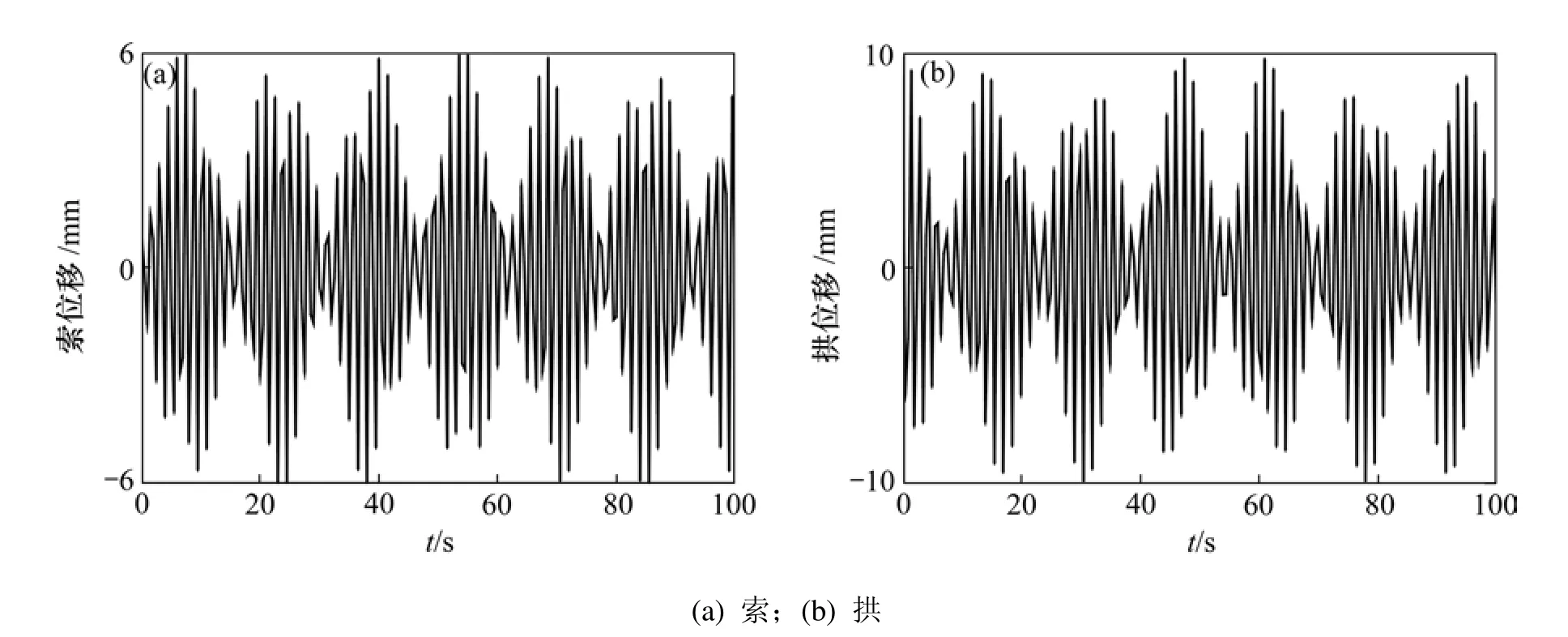
圖3 索拱組合結構內共振情形下的時間歷程Fig.3 Time history of cable-stayed arch under internal resonance state

從數值分析結果可知：在非內共振情況下，索和拱的最大振幅都與初始位移基本相同，分別為9.7 mm和 9.8 mm；而在內共振情況下，索的最大振幅達到60.5 mm，拱的最大振幅為9.9 mm。說明在內共振情況下，拱對索的激勵效果非常明顯，導致拉索產生大幅度振動，而索對拱的激勵很小，基本上可以忽略。其主要原因是索拱相互激勵的效果與索拱之間的單位質量比、抗壓剛度比及抗彎剛度比等有密切關系。

4 結論

(1) 利用索拱組合結構的連接條件及邊界條件，建立了索拱組合結構的非線性動力耦合運動學控制方程。

(3) 當索拱組合結構的結構設計參數都在非共振區域時，索和拱的動力學性質均可單獨進行分析，并可不考慮耦合作用。

(4) 當結構設計參數在索和拱的內共振區域時，在設計過程中，索與拱之間的相互耦合作用是不容忽視的關鍵問題。

(5) 在索拱內共振時，一般可以忽略索對拱的激勵，但不能忽略拱對索的激勵，其激勵效果與索拱之間的單位質量比、抗壓剛度比及抗彎剛度比等有關。

[1]趙雷, 杜正國. 大跨度鋼筋混凝土拱橋鋼管混凝土勁性骨架施工階段穩定性分析[J]. 西南交通大學學報, 1994, 29(4):446?452.ZHAO Lei, DU Zheng-guo. Analysis of stability during construction of the steel-tube concrete stiff skeleton of long-span RC arch bridge[J]. Journal of Southwest Jiaotong University,1994, 29(4): 446?452.

[2]陳寶春, 孫潮. 石潭溪大橋施工受力分析[J]. 中國公路學報,1998, 11(4): 51?57.CHEN Bao-chun, SUN Chao. Mechanic analysis of the construction phase of Shitanxi bridge[J]. China Journal of Highway and Transport, 1998, 11(4): 51?57.

[3]盛洪飛, 郭偉, 王銳, 等. 無風撐鋼管混凝土中承拱橋非線性試驗分析[J]. 哈爾濱建筑大學學報, 1997, 30(4): 103?108.SHENG Hong-fei, GUO Wei, WANG Rui, et al. The nonlinear analysis of concrete filled steel tubular half trough arch bridge without wind brace[J]. Journal of Harbin University of Architecture, 1997, 30(4): 103?108.

[4]陳寶春, 徐愛民, 孫潮. 鋼管混凝土拱橋溫度內力計算時溫差取值分析[J]. 中國公路學報, 2000, 13(2): 52?56.CHEN Bao-chun, XU Ai-min, SUN Chao. Analysis of thermal difference magnitude in thermal inner force calculation of CFST arch bridge[J]. China Journal of Highway and Transport, 2000,13(2): 52?56.

[5]趙長軍, 王鋒君, 陳強, 等. 大跨度鋼管混凝土拱橋空間穩定性分析[J]. 公路, 2001(2): 15?17.ZHAO Chang-jun, WANG Feng-jun, CHEN Qiang, et al.Analysis of space stability of steel pipe concrete arch bridge with large span[J]. Highway, 2001(2): 15?17.

[6]劇錦三, 郭彥林. 索?拱結構的平面內穩定性研究[J]. 建筑結構學報, 2001, 22(2): 84?87.JU Jin-san, GUO Yan-lin. Instability behavior in the plane of cable-arch structure[J]. Journal of Building Structures, 2001,22(2): 84?87.

[7]趙躍宇, 康厚軍, 王連華, 等. 索?拱結構面內穩定性研究[J].湖南大學學報: 自然科學版, 2006, 33(3): 1?5.ZHAO Yue-yu, KANG Hou-jun, WANG Lian-hua, et al.Instability behavior in the plane of cable-arch structure[J].Journal of Hunan University: Natural Science, 2006, 33(3): 1?5.

[8]方淑君, 李德建, 曾慶元. 三線鐵路預應力連續梁橋列車?橋梁時變系統空間振動分析[J]. 中南大學學報: 自然科學版,2008, 39(2): 394?399.FANG Shu-jun, LI De-jian, ZENG Qing-yuan. Stochastic space vibration analysis of prestressed continuous bridge time-varying system in three-track railroad[J]. Journal of Central South University: Science and Technology, 2008, 39(2): 394?399.

[9]Matsumoto M, Shiraishi N, Shirato H. Rain-wind induced vibration of cables of cable-stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41/44:2011?2022.

[10]汪至剛, 孫炳楠. 斜拉索的參數振動[J]. 土木工程學報, 2002,35(5): 28?33.WANG Zhi-gang, SUN Bing-nan. Parametric vibration of the cable in cable-stayed bridge[J]. China Civil Engineering Journal,2002, 35(5): 28?33.

[11]趙躍宇, 呂建根. 索?拱組合結構中斜拉索的非線性參數振動[J]. 土木工程學報, 2006, 39(12): 67?72.ZHAO Yue-yu, Lü Jian-gen. Non-linear parametric vibration of cables in cable-arch composite structures[J]. China Civil Engineering Journal, 2006, 39(12): 67?72.

[12]王連華, 趙躍宇. 受支承運動作用的拉索大幅振動[J]. 土木工程學報, 2008, 41(8): 65?71.WANG Lian-hua, ZHAO Yue-yu. On the large amplitude vibrations of stay cables induced by support motions[J]. China Civil Engineering Journal, 2008, 41(8): 65?71.

[13]XU Jian-xue, HUANG Hong, ZHANG Pei-zhen. Dynamic stability of shallow arch with elastic Supports-application in the dynamic stability analysis of inner winding of transformer during short circuit[J]. International Journal of Non-linear Mechanics,2002, (37): 909?920.

[14]Lakrad F, Schiehlen W. Effects of a low frequency parametric excitation[J]. Chaos, Solitons and Fractals, 2004(22):1149?1164.

[15]Pinto O C, Goncalves P B. Active non-linear control of buckling and vibrations of a flexible buckled beam[J]. Chaos, Solitons and Fractals, 2002(14): 227?239.

[16]呂建根. 大跨度索拱組合體系非線性靜動力性能研究[D]. 長沙: 湖南大學土木工程學院, 2007.Lü Jian-gen. The research on nonlinear static-dynamic mechanics performance of long-span cable-stayed arch system[D]. Changsha: School of Civil Engineering, Hunan University, 2007.