T-代數上的 Yetter-Drinfeld模范疇＊

胡曉飛

(金華職業技術學院師范學院,浙江金華 321007)

0 引 言

設π是一個離散群.Turaev[1]引進了模的 crossedπ-范疇 (根據文獻[2]簡稱為 T-范疇),并且證明了這一范疇能提升到帶有目標空間 K(π,1)的三維同倫量子場理論.文獻[2]介紹了 T-余代數上的左右 Yetter-Drinfeld模的概念和辮子 T-范疇的概念,它是 Hopf代數上的 Yetter-Drinfeld模的推廣;文獻[3]研究了T-余代數上的 Yetter-Drinfeld模的各種性質.本文討論 T-代數上的 Yetter-Drinfeld模范疇,并構造了一個辮子結構,使其成為辮子張量 T-范疇.

1 基本概念

本文中 k是一個固定的域,所有的線性空間指域 k上的線性空間,張量積 A?kB記為 A?B,張量積中的∑號省略,并采用文獻[4-5]的記號.

定義 1[2]一個 T-代數 H是指滿足以下條件的一族余代數{(Hα,Δα,εα)}α∈π:

1)一族余代數同態 m={mα,β:Hα?Hβ→Hαβ}α,β∈π(乘法 )是結合的,即對 ?α,β,γ∈π,

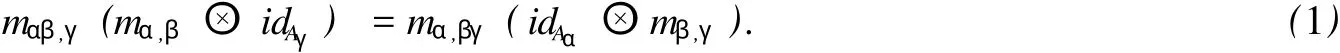
式 (1)中,id是恒等映射.對 ?α,β∈π,a∈Hα,b∈Hβ,令 mα,β(a?b)=ab,那么式 (1)可以改寫為:對 ?α,β,γ∈π,a∈Hα,b∈Hβ,c∈Hγ,(ab)c=a(bc).

2)余代數同態 u:k→A1(單位 ),使 u(1k)=1,滿足 m1,α(1?a)=a=mα,1(a?1),即對 ?α∈π,a∈Hα,1∈H1,1a=a1=a.

3)一族映射 S={Sα:Hα→Hα-1}(對極 )使得對 ?α∈π,

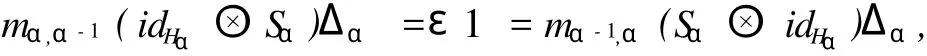
即對 ?α∈π,hα∈Hα,有

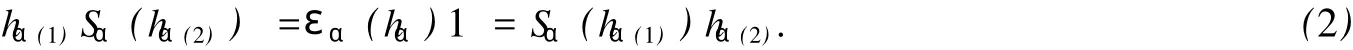
4)一族余代數同構φ={φαβ:Hα→Hβαβ-1}(φαβ常寫成φβ),對 ?α,β,γ∈π,hα∈Hα,gβ∈Hβ,滿足

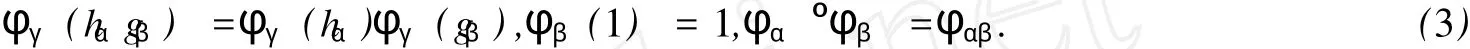
定義 2 設 H為 T-代數,M 為線性空間,稱 M 為左 π-H-模,若對 ?λ1,λ2∈π,m ∈M,hλ1∈Hλ1,hλ2∈Hλ2,存在ωλ:Hλ?M →M,記ωλ(hλ?m)=hλ·m,滿足

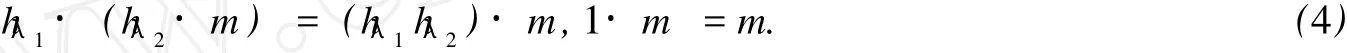
定義 3 設α∈π,(Hα,Δα,εα)為余代數,M 為線性空間,右 Hα-余模 (M,ρ)是指存在映射 ρ:M →M ?Hα滿足

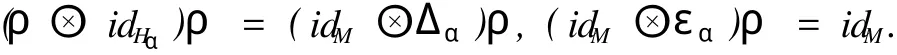
若對?m∈M,記ρ(m)=m(0)?m(1),則上述條件為:對?m∈M,滿足

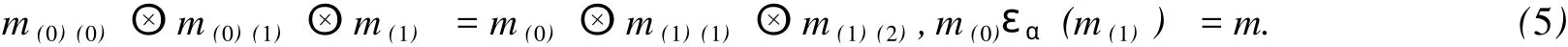
定義 4 設α∈π,H為 T-代數,左右α-Yetter-Drinfeld模 (M,·,ρ)是指 (M,·)為左π-H-模,(M,ρ)為右 Hα-余模,且對 ?λ∈π,hλ∈Hλ,m∈M,滿足

全體左右α-Yetter-Drinfeld模及其模同態構成一個范疇,稱為左右α-Yetter-Drinfeld模范疇,記為HYDHα,設HYDH表示HYDHα(對所有的α∈π)的無交并.

定義 5[2]一個范疇 T稱為 T-范疇 (π上的),如果還滿足以下條件:

1)T是一個張量范疇;

2)存在一族子范疇 {Tα}α∈π,使得 T是這族子范疇的無交并,且對 ?α,β∈π,U∈Tα,V∈Tβ,滿足U ?V ∈Tαβ;

3)記 Aut(T)為 T到自身的可逆嚴格張量函子組成的群,群同態φ:π→Aut(T)(稱為共軛)為φ(β)=φβ,滿足對 ?α,β∈π,φβ(Tα)=Tβαβ-1.

定義 6[2]T-范疇 T稱為辮子 T-范疇,若賦予了一個辮子.其中辮子是一族同構 c={cU,V:U?V→UV?U}U,V∈T滿足條件:對 ?α,β∈π,f∈Tα(U,U′),g∈T(V,V′),U,V,W∈T,

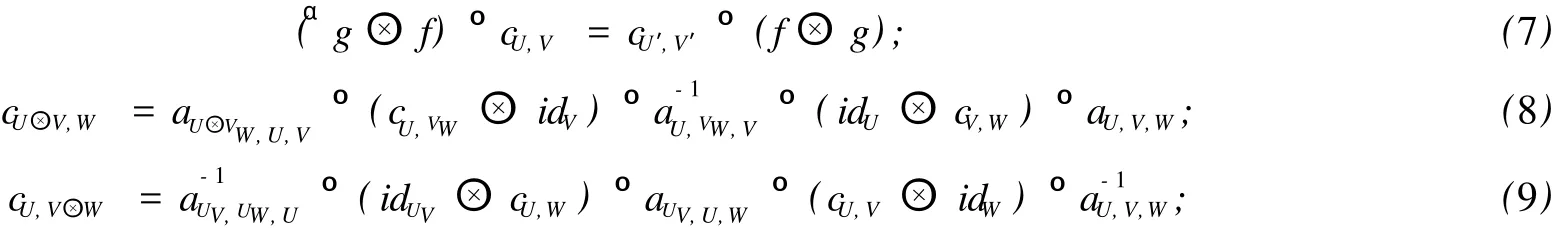
2 T-代數上的 Yetter-Drinfeld模范疇

接下來將討論 T-代數上 Yetter-Drinfeld模范疇的性質,同時證明 T-代數上的 Yetter-Drinfeld模范疇HYDH是辮子 T-范疇.

引理 1 設 H=({Hα,Δα,εα}α∈π,m,u,S,φ)為 T-代數,則對 ?α,β∈π,hα∈Hα,gβ∈Hβ,下列等式成立:

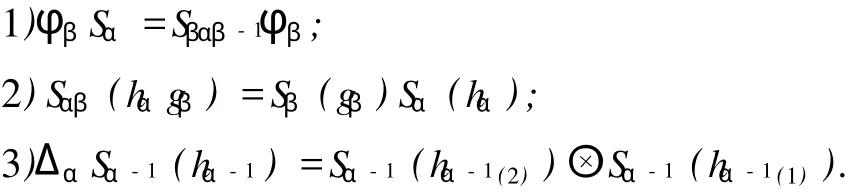
定理 1 設 α,β∈π,H為 T-代數,(M,·,ρM)∈HYDHα,(N,·,ρN)∈HYDHβ,則 M ?N ∈HYDHαβ.其中M ?N的左π-H-模和右 Hαβ-余模結構定義如下:對 ?λ∈π,hλ∈Hλ,m∈M,n∈N,

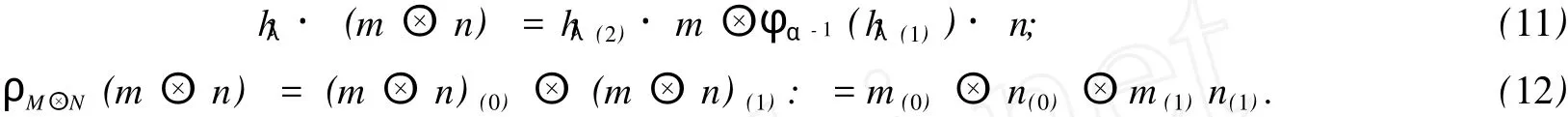
式 (12)中:ρM(m)=m(0)?m(1);ρN(n)=n(0)?n(1).

證明 易證 (M ?N,·,ρM?N)是右 Hαβ-余模和左 π-H-模.

下證 (M?N,·,ρM?N)滿足相容條件 (式 (6)).根據式 (3)、式 (6)、式 (11)和式 (12)可得

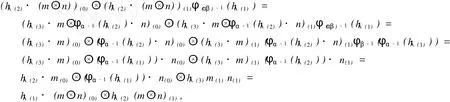
即證明了 M ?N∈HYDHαβ.定理 1證畢.

設 (M,·,ρN)∈HYDHα,對 ?β∈π,βM定義如下:作為線性空間βM=M,將 ?m ∈M 在βM 中記為βm(即βm=m),βM 的左 π-H-模和右 Hβαβ-1-余模結構分別為 :對 ?λ,β∈π,hλ∈Hλ,βm ∈βM,

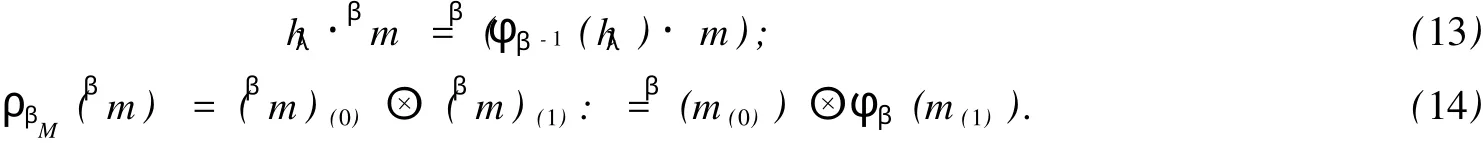
由此可得定理 2.

定理 2 設 H為 T-代數 ,M ∈HYDHα,則對 ?β∈π,βM=(βM, ·,ρβM)∈HYDHβαβ-1.特別地 ,β-1(βM)=β(β-1M)=M.

證明 易證 (βM,·)是左 π-H-模和 (βM,ρβM)是右 Hβαβ-1-余模.

下證βM滿足相容條件 (式 (6)).事實上,對 ?λ,β∈π,hλ∈Hλ,βm∈βM,根據式 (3)、式 (6)、式 (13)和式(14)得

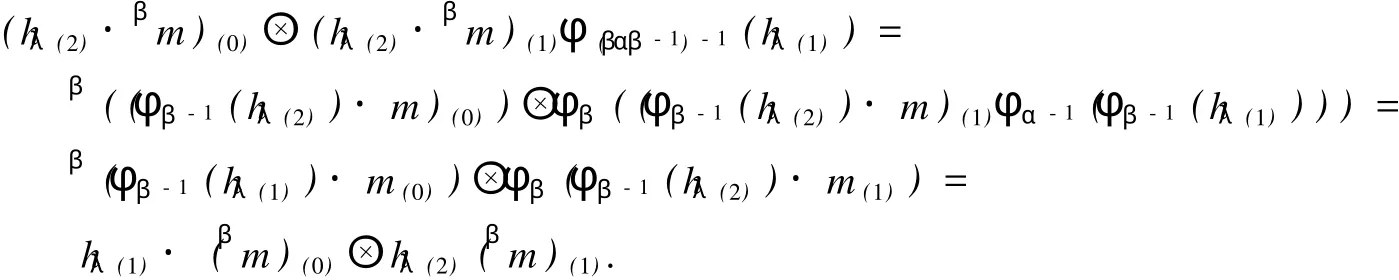
因此 ,(βM,·,ρβM) ∈HYDHβαβ-1.定理 2證畢.

另外,定義φ:π→Aut(HYDH)為β→φβ,其中φβ(M)=βM,則易證φβ為函子且φ為群同態,根據定義 5、定理 1及定理 2,即可得到定理 3.

定理 3 設 H為 T-代數,則范疇HYDH是一個 T-范疇.

定理 4 設 H為 T-代數,M∈HYDHα,N∈HYDHβ,定義

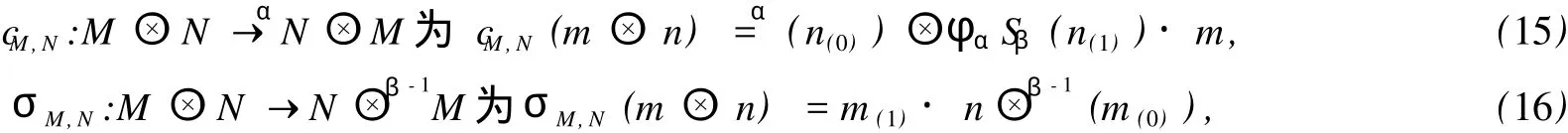
則 cM,N是 Yetter-Drinfeld模同構,它的逆同構為σαN,M.

證明 首先證明 cM,N是左π-H-模同態.由式 (2)、式 (6)、式 (11)、式 (13)、式 (15)及引理 1可得,對?λ∈π,hλ∈Hλ,m∈M,n∈N,

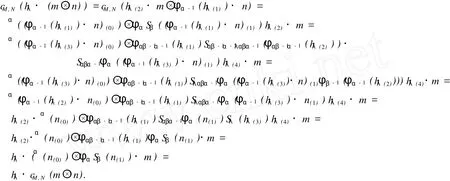
其次證明 cM,N是右 Hαβ-余模同態.事實上,對 ?α,β∈π,m ∈M,n∈N,由式 (2)、式 (3)、式 (5)、式 (6)、式 (12)、式 (14)及引理 1可得

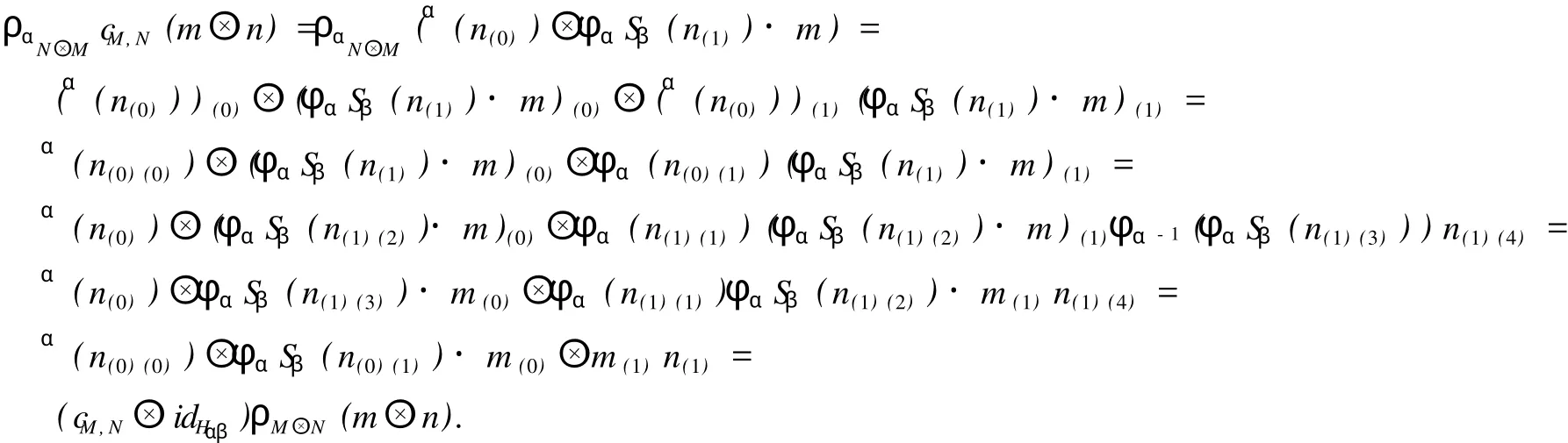
為此,cM,N是 Yetter-Drinfeld模同態.類似可證,σM,N也是 Yetter-Drinfeld模同態.又因為

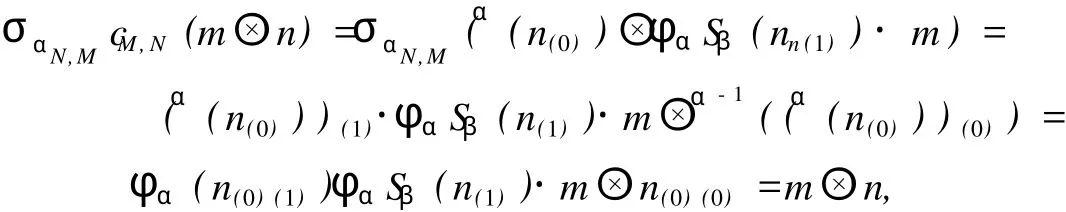
同理 cN,β-1MσM,N(m?n)=m?n,所以,cM,N是 Yetter-Drinfeld模同構,它的逆同構為σαN,M.定理 4證畢.

定理 5 設 H為 T-代數,則范疇HYDH是一個辮子張量 T-范疇,它的辮子結構 c={cM,N:M?N→αN?M}M,N∈HYDH如定理 4.

證明 只需證明式 (7)～式 (10)成立即可.對 ?α∈π,f∈HYDHα(M,M′),g∈HYDHβ(N,N′),m∈M,n∈N,有

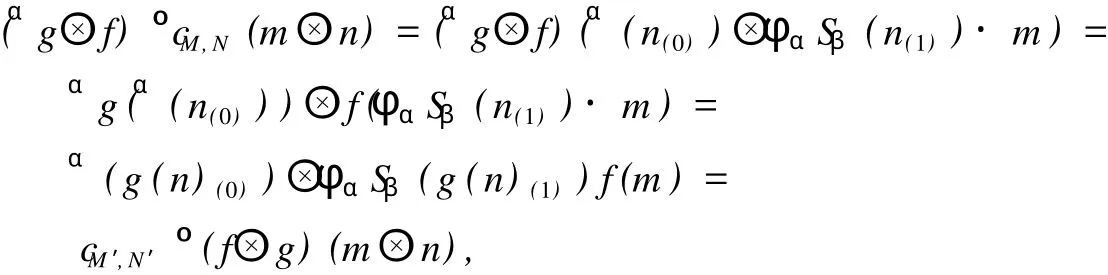
即式 (7)成立.對 ?α,β,γ∈π,M∈HYDHα,N∈HYDHβ,X∈HYDHγ,m∈M,n∈N,x∈X,根據式 (5)和引理 1有

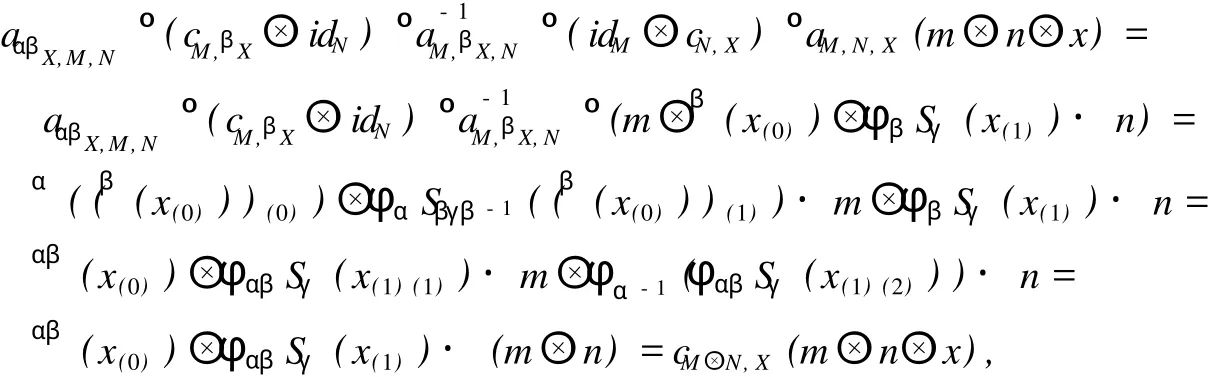
即式 (8)成立.類似可證式 (9)成立.對 ?α,β,γ∈π,M∈HYDHα,N∈HYDHβ,m∈M,n∈N,由式 (13)可得

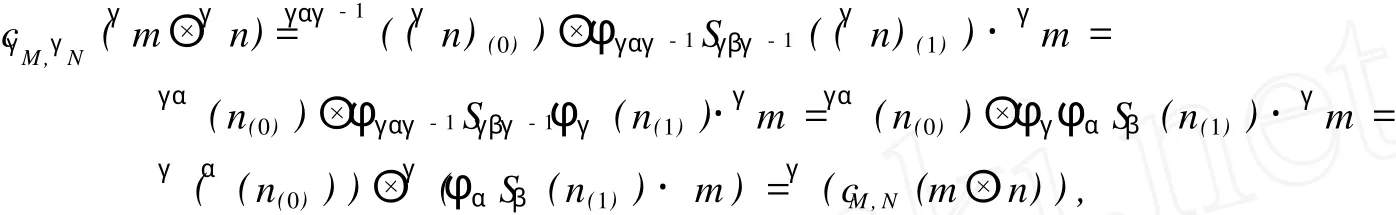
即式 (10)成立.所以,范疇HYDH是一個辮子張量 T-范疇.

3 結 語

給出 T-代數上的 Yetter-Drinfeld模范疇的結構,研究了其上的各種性質;同時還運用了有別于文獻[2]的方法,通過一系列的構造直接證明HYDH是辮子 T-范疇.

致謝:衷心感謝李金其教授的悉心指導!

[1]TuraevV G.Homotopy field theory in dimension 3 and crossed group-categories[ED/OL].(2000-05-31)[2009-06-29].http://arxiv.org/PS_cache/math/pdf/0005/0005291v1.pdf.

[2]ZuninoM.Double construction for crossed Hopf coalgebra[J].J Algebra,2004,278(1):43-75.

[3]李金其.T-余代數上的 Yetter-Drinfeld模范疇[J].浙江大學學報:理學版,2006,33(6):606-609.

[4]SweedlerM E.HopfAlgebra[M].New York:Benjamin Inc,1969.

[5]VirelizierA.Hopf group-coalgebras[J].J Pure ApplAlgebra,2002,171(1):75-122.