亞純函數的一類值分布問題

葉枝宏,何萍

(1.思茅師范高等專科學校,云南 普洱 665000;2.紅河學院數學學院,云南 蒙自 661100)

亞純函數的一類值分布問題

葉枝宏1,何萍2

(1.思茅師范高等專科學校,云南 普洱 665000;2.紅河學院數學學院,云南 蒙自 661100)

本文利用筆者在文獻[3]中構造的亞純函數否定了一類特殊的亞純函數退化為有理函數,同時用Albert Edrei在文獻[4]中所構造的亞純函數的性質否定了一個整函數的值分布問題推廣到亞純函數的可能.

有理函數;亞純函數;角域;射線;級與下級

0 引言

對于判定整函數f∞(z)何時退化為多項式方面,文獻[1]中介紹:如果存在一無界數列(z)=ωn}位于一條從原點出發的射線上,此時f(z)為次數不超過2的多項式.在1993年,喬建永在文獻[2]中得到:若對某自然數m有且存在一無界數列使得位于上,這時f(z)是次數不超過2m的多項式.

在考察亞純函數情形時,自然會提出下述問題:

1 主要結論

為回答這一問題,本文得到如下定理:

定理1若f(z)為下級有窮的超越亞純函數,存在一無界數列使得f(z)=ωn的根只位于Ω(-ε0,ε0)內.(這里ωn依賴于

證明:考察下級為零級的亞純函數(參見筆者在文獻[3]中的詳細介紹)

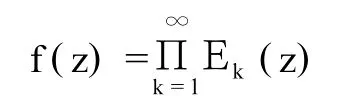
對于該函數而言,在Ω(-ε0,ε0)外,若取定充分小ε0(0＜ε0＜1),同時考慮角域C/Ω上函數f(z)的模.其Ω=Ω(-ε0,ε0).

此時對于?z?C/Ω和一切的k?N有

p=b1sinε0≤|z-bk|

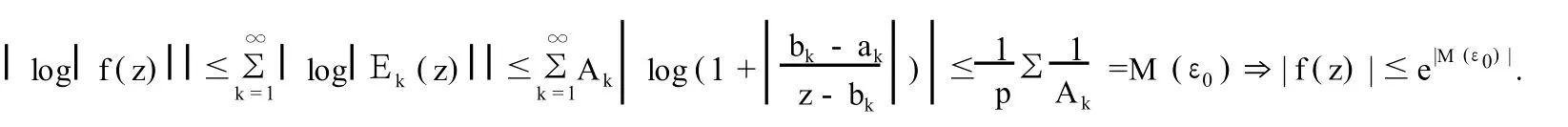
2 結論的應用

對于問題,Albert Edrei在文獻[4]中介紹了函數

該函數顯然是極點只位于正實軸上的亞純函數.若取定一無界正實數列,此時對于Im z≠0,有

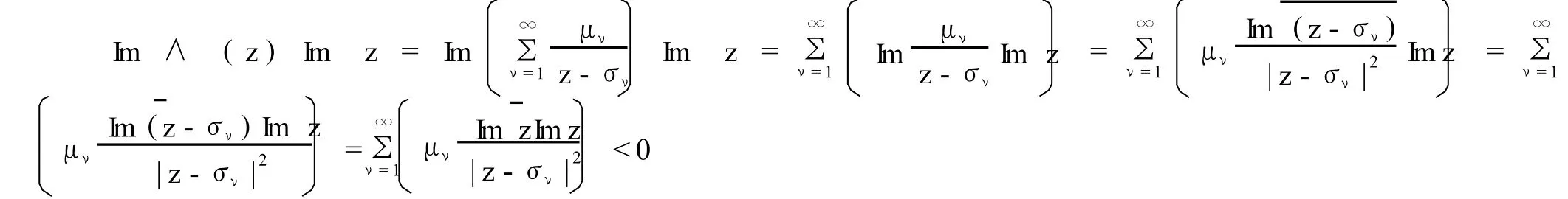
[1]Baker,In,&Liverpool l.s.o.The value distribution of entire funtions of order atmost one[J].Acta Sci,Math.,41(1979):3-14.

[2]喬建永.整函數的值分布與集[J].數學學報,1993,36(3):418-422.

[3]葉枝宏.零點和極點位于有限條射線上的亞純函數[J].云南師范大學學報,2007,1:101-103.

[4]Albert Edrei.Meromorphic functions with three radially distributed values[J].Amerrica Mathematical Society,1955,78(2):277-293.

The Problem s of The Value Distribution about Meromorphic Functions

YE ZhiHong1,HE Ping2
(1.Teacher College of Mathematics,Simao 665000,China;2.Department of Mathematics,Honghe University,Mengzi 661100,China)

In this paper,we use a function which is structured in[3]and deny meromorphic Functions to degenerate rational function.At the same time,the value distribution of entire functions to extend meromorphic functions is denied by a function which was constructed by Albert Edrei in[4]

Rational Functions;Meromorphic Functions;Angular Domain;Rays;Order and Lower Order

0174.52

A

1008-9128(2010)02-0034-02

2009-11-30

紅河學院博士、碩士科研啟動項目(XSS08013)

葉枝宏(1980-),男,云南普洱人,碩士,助教.研究方向:復分析.

[責任編輯 宋煥斌]