利用最短路徑算法確定地理網絡中心服務范圍

胡于杰,李 響

(華東師范大學地理信息科學教育部重點實驗室,上海 200062）

利用最短路徑算法確定地理網絡中心服務范圍

胡于杰,李 響

(華東師范大學地理信息科學教育部重點實驗室,上海 200062）

設施服務范圍指在一定限制條件下(如時間、費用或路程等）設施所能提供服務的最大空間領域,在道路網絡環境中,它通常由一系列結點及邊組成[1]。例如,某救助站在接到求救電話后10 min所能到達的區域;某物流公司在配送貨物時500元花費所能到達的區域等。在GIS中稱尋找這類區域的問題為中心服務范圍問題。對于中心服務范圍的研究有助于解決消防站、學校及醫院等公共設施的服務范圍劃分問題。傳統方法(如廣度優先遍歷算法）通常用以服務設施所在位置為中心、以時間(或距離）為半徑形成的圓形區域所構成的等時區(或等距區）表示服務范圍。這種表示方法用直線距離評價通達性,只是一個概略的結果[2],不能反映從服務設施到需求點的實際通達情況。為此,本文在總結中心服務范圍典型算法的基礎上,提出利用最短路徑算法確定中心服務范圍的方法。

1 地理網絡中心服務范圍的形式化定義

中心服務范圍是指從中心點出發,在限定條件下可達的區域,由一系列結點及邊構成的網絡子集:

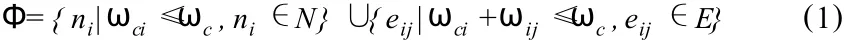
其中,c代表網絡的某個中心,N代表網絡的結點集合,E代表邊集合,ωc代表網絡中心的限制費用,ωci為中心點c至網絡結點i的累計費用,ωij為邊eij的費用[3]。

從中心出發任意路徑的費用不能超過中心的限制費用。在實際生活中,這種費用可以是時間、路程及花費的金錢等。

2 利用最短路徑算法確定地理網絡中心服務范圍

2.1 數據存儲結構

本文利用自定義的類結構存儲網絡結點及網絡邊,描述如下(為便于描述,下文將“費用”理解為“阻值”）:

該結構可以完整地反映網絡中結點與其鄰接結點及邊的關系,能很好地反映網絡的拓撲關系。在此基礎上構建了結點間的關聯矩陣,用于最短路徑算法。

2.2 最短路徑算法

本算法是對Dijkstra最短路徑算法[4]的改進(簡稱“最短路徑算法”）。首先,將網絡中所有結點初始化為未標記結點,除中心外所有結點的阻值(即費用）賦為無窮大。然后從起點(第一次搜索的起點為網絡中心）開始搜索與其有路徑連通的未標記結點,賦以合理的阻值,并將起點標記為已標記結點,再以阻值不為無窮大的未標記結點為起點開始搜索,重復上述過程,直到某結點的阻值超過網絡中心的阻值或所有結點均為已標記結點為止。最后,基于結點及邊的阻值搜索并存儲所有在中心阻值范圍內的邊,這些邊和結點的集合為網絡中心的服務范圍。結合2.1中的數據結構,算法描述如下:

(1）將所有結點的dist置為∞,pre_node置為null,ischecked置為false;將起點from_node的dist置為0;定義網絡中心阻值為distance。

(2）定義變量M IN_ID,用于存儲每次搜索過程中起點的編號;定義變量M IND,用于存儲上述結點的阻值。1）判斷所有結點ischecked屬性,若全為true,則跳出第2步;2）在所有ischecked屬性為false的結點中搜索,若某結點nodei滿足nodei.dist＜∞,則M IND=nodei.dist,M IN_ID=nodei. id;3）判斷M IND與網絡中心阻值distance的大小,若前者大于后者,則跳出第2步;4）令nodeMIN_ID.ischecked=true;5）在所有結點中搜索與編號為M IN_ID的結點有路徑連通的結點nodej,若nodej.dist＞M IND+arck.im pedence(其中arck代表以nodei為起點,nodej為終點的邊,編號為k）,則令nodej.dist=M IND+arck.im pedence;nodej.pre_node=nodeMIN_ID。

(3）對所有已標記結點進行判斷。1）若網絡中某條邊arck滿足如下關系:arck.node_from.id==from_node.id或arck.node_to.id==from_node.id,且arck.im pedence＜distance,則將邊arck加入結果集中,即arck.isA dded=true;2）若邊arck滿足如下關系:arck.node_from.dist+arck.impedence＜distance或arck.node_to.dist+arck.im pedence＜distance,則將邊arck加入結果集中,即arck.isA d ded=true。

本算法第1步為搜索過程初始化,第2步為結點賦阻值,第3步搜索并存儲所有在中心阻值范圍內的邊。其中,即使某結點的ischecked屬性為true,它仍可參加為其鄰接結點賦最小阻值的運算過程,因此將不會產生“漏邊”現象;而廣度優先遍歷算法在某結點被訪問后,后續的遍歷過程將不再考慮該結點,有可能產生“漏邊”現象,需要大量的后續處理來彌補,從而增加了算法的運算時間。

3 應用實例

以美國加利福尼亞州部分縣的道路交通網絡為例,結合面向對象語言C#及A rcGIS Engine設計實現了利用最短路徑算法確定地理網絡中心服務范圍系統,通過輸入網絡的中心及相應的阻值(本實驗中為距離）,所有在中心服務范圍內的道路均在地圖上高亮顯示。

在主頻為3.0 GHz、內存為2 G、硬盤為160 G的環境中針對7組不同的數據進行實驗,其數據量依次增大(表1）。為了比較結果的準確性及算法的運算效率,針對每組數據,隨機選擇一個網絡結點作為中心位置,同時給定一個40 km的中心阻值,將最短路徑算法和廣度優先遍歷算法[3]分別應用于上述7個數據集中,在道路網絡數據量不斷增大的情況下,兩種算法的運算時間如圖1a所示。

表1 實驗用的7組數據

由圖1a可知,隨著道路網絡數據量的增大,兩種算法在計算網絡中心服務范圍過程中的運算時間逐漸增長。其中,最短路徑算法的運算時間增長平穩,而廣度優先遍歷算法卻出現了明顯的“拐點”,自該拐點后,運算時間增幅急劇增大。以第7組數據集為例,最短路徑算法的運算時間僅為廣度優先遍歷算法的4.9%,大幅提高了運算效率。為進一步分析中心阻值對算法運算效率的影響,選取第5組道路網絡,并隨機選取一個網絡結點作為中心位置,依次給出25組數據,運行上述兩種算法,比較運算時間,結果如圖1b。

由圖1b可知,當網絡中心阻值小于14 km時,兩種算法的運算時間基本接近;當網絡中心阻值大于14 km后,隨著網絡中心阻值的增大,二者的運算時間均不斷增長,但廣度優先遍歷算法的運算時間明顯比最短路徑算法的運算時間增幅大,且增幅隨著網絡中心阻值的增大不斷變大。以中心阻值56 km為例,最短路徑算法的運算時間僅為廣度優先遍歷算法的2.6%。

此外,為了解網絡形態對算法運算效率的影響,同樣以第5組網絡數據為研究對象,通過給定中心阻值,變換中心位置,觀察運算時間的變化。實驗中,以道路網絡不同區域的稠密程度來展現不同的網絡形態,城市道路網密度是城市道路中心線總長度與城市用地面積之比[5],基于此定義,得到網絡內不同區域的密度(表2）,在密度不同的區域中隨機選擇7個網絡中心,并隨機給定中心阻值36 km,分別利用兩種算法計算網絡中心服務范圍,運算時間如圖1c所示。

表2 7組數據所處區域的道路網絡密度

圖1 最短路徑算法和廣度優先遍歷算法運算時間比較

以道路網絡密度4 km/km2為界,根據表2可知,編號為1 378、2 498、3 007、5 261的點位于網絡的稠密區,而其他3點位于網絡的稀疏區。結合實際情況可得如下結論:在本組實驗條件下,最短路徑算法的運算效率比廣度優先遍歷算法高。以網絡中心編號1 378的點為例,最短路徑算法的運算時間為廣度優先遍歷算法的3.3%,而且,隨著中心所處區域網絡密度的變化,相對于廣度優先遍歷算法而言,最短路徑算法的運算時間基本不變。

4 結論

本文提出了一種基于最短路徑算法計算地理網絡中心服務范圍的新方法,針對同一網絡數據集,最短路徑算法比廣度優先遍歷算法所需時間更短,隨著網絡尺度或中心阻值的增大,二者運算時間均有提高,但廣度優先遍歷算法運算時間增幅遠高于最短路徑算法;當網絡中心位置發生變化時,最短路徑算法比廣度優先遍歷算法所需運算時間更少,運算效率更穩定。

本文提出的方法僅適用于單個中心服務范圍的劃分問題,當網絡中存在多個中心點時,一種方法就是將其作為多個單中心問題分別解決,但當服務范圍間存在競爭關系時,需同時考慮多個中心的影響,這將成為進一步的研究方向。

[1] 白玲,王家耀.基于GIS的地理網絡模型研究[J].信息工程大學學報,2000,1(4）:96-98.

[2] 龔潔暉,白玲.確定地理網絡中心服務范圍的一種算法[J].測繪學報,1998,27(4）:357-362.

[3] 史照良,黃繼安.基于特征的非平面 GIS-T數據模型在中心服務范圍中的應用[J].現代測繪,2004,27(1）:3-6.

[4] D IJKSTRA E W.A note on two p roblem s in connexion w ith graphs[J].Numerische Mathematik,1959,1:269-271.

[5] 沈建武,吳瑞麟.城市道路與交通[M].武漢:武漢大學出版社, 2006.104-105.

2009-12-14;

2010-03-03

胡于杰(1987-）,男,碩士,研究方向為空間覆蓋模型及優化算法。E-mail:hueujee@mail.com