巧用Excel分析評價英語試卷
張維維
摘要:Excel 是大家熟悉的辦公軟件,利用Excel 可以輕松完成復雜的試卷質量分析與評價。從而使英語教師對整個教學過程有一個全面、系統、科學的認識,為強化教學監控與提高教學質量提供準確化、科學化的量化依據。
關鍵詞:Excel; 英語試卷; 測試; 統計分析
目前,90%的初中每周會有一次單元測驗,再加上月考,期中考,期末考,教師僅憑手工進行數據資料的整理和計算,工作繁重枯燥,只能提供考生的考試分數、平均分和及格率等基本考試情況。
利用Excel 可以輕松完成復雜的試卷質量分析與評價。
在教育統計學中,對統計資料的處理分為三個步驟進行:第一步是全面而準確地收集客觀數據資料;第二步是整理數據資料;第三步是統計資料的計算和分析。
一、數據資料的計算和分析
數據資料的收集和整理以后,為了更客觀地解釋考生分數,更好地了解教學班的考試情況,一般通過如下幾個統計參數進行計算和分析,在此舉例說明。
下例對某班一次“英語單元測試”成績進行統計分析,將學生成績填入Excel的單元格區域“B2:B15”中,如表1所示。
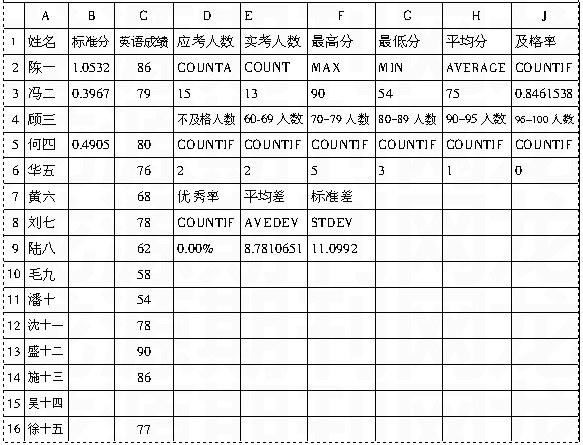
1. 班級人數。在Excel表中可用COUNT函數計算,例如:在單元格E3中填入公式=COUNT(B2:B15)。如果有學生缺考,應該用COUNTA函數對非數值型數據進行統計,例如:在單元格D3填入公式= COUNTA(A2:A15)。
2. 班級最高分。可用MAX函數計算,例如:在單元格F3中填入=MAX(B2:B15)。
3. 班級最低分。可用MIN函數計算,例如:在單元格中G3填人=MIN(B2:B15)。
4. 班級平均分。可用AVERAGE函數來計算,例如:在單元格H3中填入公式:AVERAGE(B2:B15)。
5. 及格率。通常將60分設定為及格線。在Excel中可用COUNTIF函數來計算,例如:在單元格J3中填入=COUNTIF(B2:B15,“>=60”)/COUNTA(A2:A15)。
6. 優秀率。初中英語教學通常將95分以上設定為優秀分。還是用COUNTIF函數來計算,例如:在單元格D9中填入=COUNTIF(B2:B15,“>=95”)/COUNTA(A2:A15)。
7.分數段。將考生成績按照高低分進行分數段的統計,可以大致了解考試出題難度組合狀況、考生成績平衡性等。在Excel中可用COUNTIF函數來統計。例如:“80—89”分數段可用公式=COUNTIF(B2:B15,“>=80”)—COUNTIF(B2:B15,“>=90”),“70—79”分數段可用=COUNTIF(B2:B15.“>=70”)—COUNTIF(B2:B25,“>=80”),“60-69”分數段可用=COUNTIF(B2:B15,“>=60”)—COUNTIF(B2:B15,“>=70”),不及格人數可用=COUNTIF(B2:B15,“<60”)進行統計,其余類似。
8. 平均差。該參數表示全班學生成績與全班平均分的絕對偏差的平均值,用于測評全部學生成績與平均分的差異情況。在Excel中可用AVEDEV函數來計算。例如:在單元格E9中填入公式=AVEDEV(B2:B15)。
9. 標準差。這是反映考生考試成績波動情況和判斷、區分考生成績的最重要的統計量。理論上認為標準差大,區分效果好,標準差小,成績分布則比較集中,通常要求將該值控制在“8—10”之間。在Excel中可用STDEV函數,例如:在單元格F9中填入公式=STDEV(B2:B15)。
10. 標準分。這是以標準差為單位,表示某一分數與平均數的差。標準分數在教育工作中的用途很多,它可以用來比較各個學生的成績在班級成績中的地位,也可以用來比較某個學生在兩種或多種測驗中所得分數的優劣。計算機可以方便的將原始分轉換成標準分,使課程之間和班級之間具有可比性,找到各班、年級在校內的位置,從而對全校教學情況一目了然。例如:計算某個學生(陳一)的標準分,在單元格中填入公式=(B2—AVERAGE(B2:B15))/STDEV(B2:B15)。
二、考卷的分析和評估
直方圖工具:以某校八年級某班期末考試成績為例,將考試成績輸入Excel表格C1:C41。該測驗最高分為100,最低分為78,先確定一個區間[77.1, 102.1] (組限通常取比數據的精度高一位,即多一位小數點或個位數,以免數據剛好落在端點上)。將區間[77.1, 102.1]等分為5個小區間,即組距△=(102.1-71.1)/ 5=5。這樣各小區間的組限端點從左至右依次為:77.1,82.1,87.1,92.1,97.1和102.1
打開EXCEL文檔,點開“工具”——“數據分析”——“直方圖”,在“輸入區域”對話窗輸入C1:C41(即學生成績所在欄),在“接受區域”輸入組限端點所在地單元格區域,選中“標志位在第一行”。即可得到直方圖:
根據直方圖,我們可以大致看出某項目(如某次測試的成績)的分布圖形,從而判定該項目所蘊涵的意義。分布圖形一共分六種:
正態分布 說明測試結果與學生的實際情況一致,各種難度的項目比例合理。
正偏態分布 說明試題難度偏高,難度較大的項目比例偏大。呈這種分布的試題有利于將
成績優秀的學生和中等程度的學生區別開,但不利于將中等程度的學生和成績較差的學生區別開。
負偏態分布 說明試題難度偏低,難度較低的項目比例偏大。呈這種分布的試題有利于將成績較差的學生和中等程度的學生區別開,但不利于將中等程度的學生和成績優秀的學生區別開。
尖峰態/陡峭型分布 說明試題中同等難度的項目較多,梯度偏小。呈這種分布的試題幾乎不能將不同程度的學生區分開,分數分布過于集中。
低峰態/平坡型分布 說明試題中各種難度的項目比例接近,梯度較大。呈這種分布的試題區分度較高,但分數之間的差異偏大。
雙峰型分布 說明試題存在兩極分化現象,即難度偏高的和難度偏低的項目較多,而中等難度的項目偏少,項目難度的分布缺乏梯度,不夠合理。呈這種分布的試題可以區別中等程度的學生,但不利于區別出成績優秀的學生和成績較差的學生。
于是我們可以得到結論:
1. 根據該班級測試的直方圖,可以判定該正態分布為負偏態分布。有利于將成績較差的學生和中等程度的學生區分開,但不利于將中等程度的學生和優秀學生區分開。
2. 該正態分布為尖峰態分布。不能將不同程度的學生區分開,分數過于集中。
參考文獻:
1. 黃光揚.《教育測量與評價》華東師范大學出版社,2002
2. 侯曉霞,王子勇.《試卷質量分析與評價系統地設計》計算機工程,2000,26(11):151-153
3. 李翠,李進才《利用Excel對試卷質量進行系統分析》集寧師專學報,2001,23(4):26-28
4. 宣仲良《Excel實現的試卷分析質量表》江蘇大學學報(高校研究版)2004,26(3):88-92

