基于最優信標組的擴展卡爾曼定位算法*

孟文超，俞 立，董齊芬，王 銘

(浙江工業大學信息工程學院，杭州310023)

無線傳感器網絡(Wireless Sensor Networks)是一門集微電子、通信、計算機和傳感器技術為一體的技術，具有廣泛的應用領域。隨著無線傳感器網絡的快速發展，傳感器節點的位置信息在WSNs的諸多應用中扮演著不可或缺的重要角色，如在環境監測、戰場偵察、目標跟蹤等應用中，監測數據只有與節點位置信息綁定才有意義［1］。另外，節點位置信息也是大多數路由協議的基礎［2－3］。

近年來，國內外學者對無線傳感網定位技術進行了深入研究。根據定位過程中是否測量節點間的距離，定位算法主要分為基于測距算法和無需測距算法［4］。無需測距的定位方法僅根據網絡的連通性來定位，定位精度在一定程序上依賴于網絡平均每跳距離的估計精度，而且當網絡的拓撲結構不規則時，算法的性能急劇下降。如DV-Hop算法、APIT算法、質心算法等［5］。基于測距的定位算法通過測量節點間距離或角度信息完成定位過程，如基于接收信號強度衰減的定位(RSSI)、基于到達時間的定位(TOA)、基于到達時間差的定位(TDOA)和基于角度的定位(AOA)。基于測距算法的定位精度一般高于無需測距算法，但一般需要額外硬件的支持［6］。

本文通過分析基于RSSI的定位技術存在的問題，提出一種新的基于最優信標組的擴展卡爾曼定位算法(BBG-EKF)。該算法在分析未知節點與信標節點的距離及信標節點間的共線性對定位精度影響的基礎上，提出一種最優信標組選擇機制，進而通過擴展卡爾曼濾波實現定位，這樣既提供了較強的環境干擾魯棒性，又沒有增加網絡通信開銷。實驗結果表明，本文提出的定位算法在定位精度、通信量和環境干擾魯棒性等方面具有優越性。

論文其余部分安排如下:第1部分，介紹基于RSSI的測距原理;第2部分，分析影響定位精度的因素，并在此基礎上提出一種選擇最優信標組機制;第3部分，引入擴展卡爾曼濾波消除RSSI測量中的環境噪聲;最后是算法仿真與總結。

1 RSSI測距模型

為適應實際環境中存在的多徑效應、繞射、障礙物等因素，本文利用RSSI值并結合傳播路徑損耗經驗模型計算未知節點到信標節點的距離。通常引入隨機干擾的對數－正態分布模型作為無線傳感器網絡路徑損耗模型［12］。

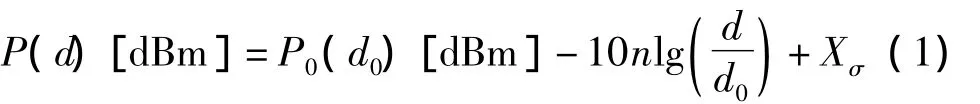
式中，d是發射節點與接收節點之間的距離，P(d)是距離為d時的接收信號強度，d0為參考距離，通常取1 m，P0(d0)是距離為d0時的接收信號強度，Xσ的均值為0、標準差為σ的高斯白噪聲，n是與環境相關的路徑損耗指數。由于不同的環境對測距有較大影響，為了得到更高的定位精度，需要針對特定的環境，通過實驗獲得相應的n和Xσ。

2 信標節點選擇

無論是基于測距的定位還是測距無關的定位，都要利用信標節點。一般來說，可選擇的信標節點信息越多，估計的位置越準確。另外，信標節點之間的位置拓撲關系及未知節點與信標節點之間的距離都在很大程度上影響定位結果。本節主要從這兩方面分析它們對定位精度的影響，為合理選擇最優信標節點提供依據。

2．1 未知節點與信標節點之間的距離

在基于RSSI測距的定位技術中，參與定位的信標節點數越多，定位精度越高。但是，當信標組中存在遠離未知節點的信標節點時，定位效果將變差。定義距離估計誤差即發射節點與接收節點的估計距離與真實距離 d的差值為，則=－d。由式(1)易得與 d、Xσ的關系式為:

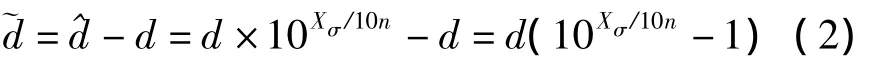
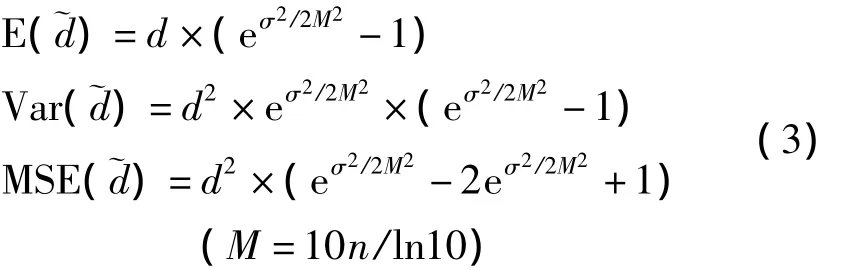
從式(3)可以看出:當RSSI測距模型中的σ2及n確定時，距離測量誤差與發射節點和接收節點間的距離成正比，距離越遠，距離測量誤差越大。為了分析距離對定位精度的影響，考慮未知節點與信標節點的距離分別從1 m至10 m變化，測距誤差隨距離變化的結果如圖1所示。

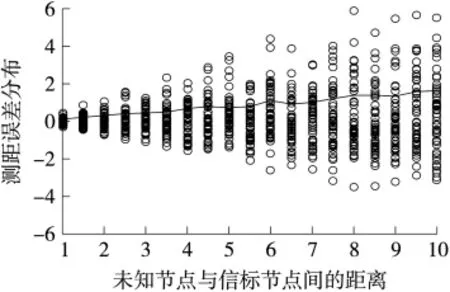
圖1 距離誤差分布

仿真結果表明:在基于RSSI的測距技術中，由于誤差的累積性，當接收節點遠離發射節點時，距離測量誤差也會隨之增加，從而影響定位精度。因此，為了優化定位效果，應選擇未知節點最近的K個信標節點進行定位。理論上，信標節點與未知節點的距離越近，RSSI值越大，所以在定位過程中，直接選擇RSSI值最大的K個信標節點。

2．2 信標節點的共線度

在二維空間中，未知節點只需獲得三個信標節點的位置信息，就可以確定自身的位置。然而，當3個信標節點共線或接近共線時，較小的測距誤差都會導致很大的定位誤差［13］。如圖2所示:當信標節點B1、B2、B3幾乎在一條直線上時，信標節點通信圓周的交點不唯一，也就無法確定未知節點究竟是在N1還是在N2。

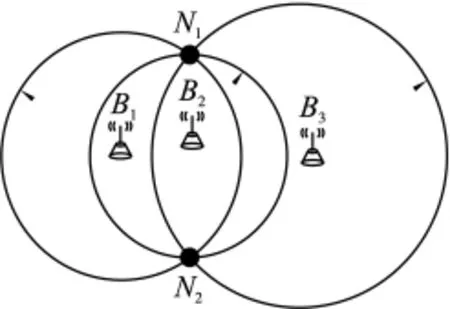
圖2 信標節點共線情況

為了解決信標節點的共線問題，引入共線度NC的定義。共線度NC定義為信標節點組成的三角形中最小角的余弦值。如圖3(a)所示，A、B、C是三個信標節點，∠A是三角形ABC中最小角，則用∠A的余弦值來衡量信標節點組的共線程度，即:

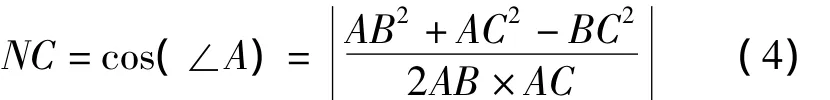
因為共線度定義為三角形最小角的余弦值，最小角的取值范圍為0°～60°，對應共線度NC的取值范圍為0．5～1。當NC值等于0．5時，代表信標節點組成的三角形是等邊三角形，此時用這組信標節點進行定位，效果最好。當NC值等于1時，代表信標節點組在一條直線上，此時定位效果最差。

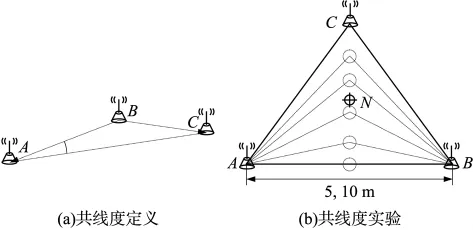
圖3 共線度的定義與實驗示意圖

如圖3(b)所示，為了分析共線度對定位精度的影響，保持信標節點A、B的距離不變，通過改變信標C的位置來獲得不同的NC值，信標節點C從AB的中點移動到三個信標節點構成等邊三角形的位置，未知節點N放置在等邊三角形ABC的中心。采用傳統的極大似然估計對未知節點N進行定位，得到共線度與定位精度的關系如圖4所示。實驗結果表明:平均定位誤差隨著共線度NC的增大而增大，當NC小于0．75時，定位性能比較穩定，而在NC大于0．75時，定位性能隨著NC的增大發生明顯惡化。為了提高定位精度，設定共線度閾值CM，篩選NC≤CM的信標節點組。

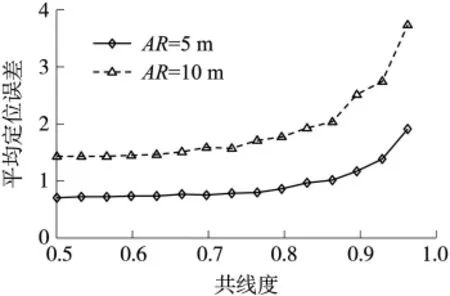
圖4 共線度與定位精度的關系

2．3 最優信標組

由以上分析可知，信標節點距離未知節點越遠，信標節點間共線度越大，未知節點的平均定位誤差越大，這為合理選擇最優信標組提供了依據，最優信標組應選擇未知節點附近共線度最小的一組信標組。

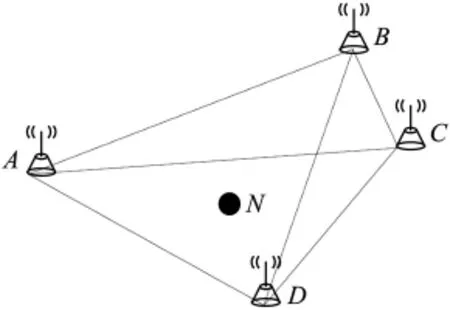
圖5 最優信標組

為減少計算復雜度，定義一組信標組包含三個信標節點。最優信標組的選擇如圖5所示，離未知節點N最近的四個信標節點分別是A、B、C、D，組成ABC、ABD、BCD、ACD等四個導標三角形，根據共線度的定義易知三角形ACD的共線度最小，為未知節點N的最優信標節點組。

3 擴展卡爾曼定位

理論上，根據上述信標選擇機制確定了最優信標組后，利用極大似然法即可得到較高精度的定位效果。然而，實際環境中，噪聲、多徑效應、非視線關系等條件的變化使得實際接收到的信號強度存在比較大的誤差，該誤差表現為高斯白噪聲，影響定位結果。卡爾曼濾波［14－15］在高斯白噪聲的動態系統中是一種最優濾波器，可以有效地抑制RSSI測量中噪聲，增強環境干擾魯棒性，提高定位精度，本節分析利用基于擴展卡爾曼的定位算法。

3．1 擴展卡爾曼模型

(1)狀態方程模型

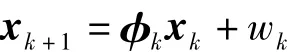
式中，xk=(xk，yk)T表示未知節點在第k－1個信標位置進行濾波計算后的坐標向量，wk是系統噪聲，服從N(0，Qk)高斯分布，φk是系統矩陣，在未知節點的定位過程中，認為未知節點的位置是固定的，所以φk為二階單位矩陣，系統噪聲方差Qk=0。

(2)測量方程模型

文中選用未知節點到信標節點之間的距離作為EKF的測量值，測量方程為

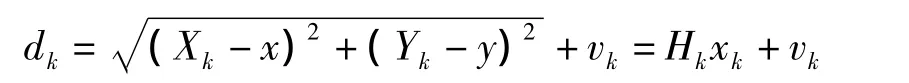
式中，di為未知節點到第i個信標節點的距離，它是根據1節描述的測距方法測得，(Xi，Yi)是第i個信標節點的坐標，(x，y)是未知節點的坐標，vi是測量噪聲，服從均值為零，方差為R的高斯分布。通過在平衡點展開泰勒級數對測量方程線性化處理，平衡點取上一次濾波后未知節點的坐標向量，線性化后的測量方程為:

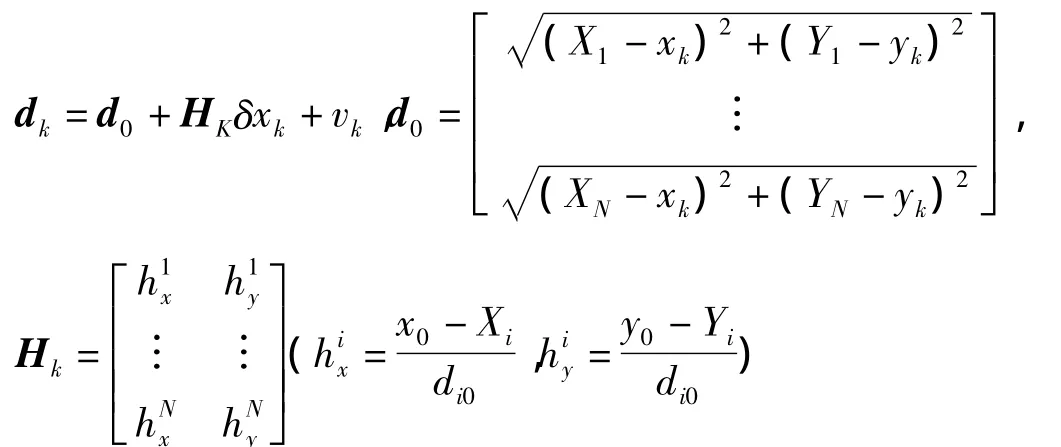
圖6 EKF定位流程圖

擴展卡爾曼定位的流程圖如圖6所示，主要包括狀態變量及誤差方差陣初始化、狀態方程及測量方程線性化、計算卡爾曼增益、更新狀態變量、預測等五個步驟。狀態初值和初始狀態誤差方差陣的正確選擇，對于EKF的收斂速度和定位精度有很大的影響，為了減少算法的復雜度，初值任意選取，而不是采用特定定位算法給出比較準確的值，但同時為加快EKF的收斂速度，本文選取比較大的初始狀態及誤差協方差。

4 算法過程

(1)信標節點周期性發送包含節點ID、位置坐標信息包。

(2)未知節點收到信標節點的信息后，對信標節點依其RSSI值從大到小排序，并建立RSSI值與未知節點到信標節點距離的映射，建立3個集合。

信標節點集合:

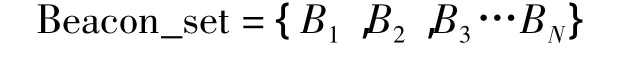
未知節點到信標節點距離集合:

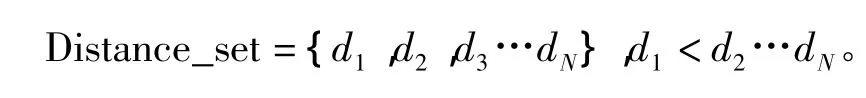
信標節點位置集合:

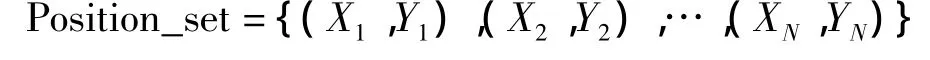
(3)未知節點首先從信標集合Beacon_set中選取離未知節點最近的4個節點，然后每3個信標節點組成一組信標組，總共可以分成C34組，分別計算各個信標組的共線度后，選取共線度最小的一組作為最優信標組。

(4)未知節點坐標向量的初值任意取定，初始狀態誤差協方差P0取值偏大些，使EKF盡快收斂于真實值。把x0，P0代入圖6的流程圖中，迭代到指定次數或者滿足定位精度要求為止。

5 仿真實驗

為了檢驗BBG-EKF算法的可行性和有效性，本部分主要對算法進行仿真。仿真在Matlab平臺上進行，默認的仿真參數P0(d0)=5，σ=4，并通過與擴展卡爾曼定位算法(EKF)、基于最優信標組的極大似然估計算法(BBG-MLE)、極大似然估計算法(MLE)做比較，分析該算法的性能。不失一般性，假設200個未知節點和一定數目的信標節點隨機部署于50 m×50 m的正方形區域C中，當未知節點通信范圍內少于3個信標節點，采用弗洛伊德算法(Floyd Algorithm)獲得與其它信標節點的最短距離。

圖7是通信半徑R=15、信標節點數M=20時BBG-EKF的定位效果，其中圓圈表示未知節點，方塊表示信標節點，直線連接未知節點的真實坐標和它的估計坐標，直線越長，定位誤差越大。仿真結果表明:BBG-EKF的平均定位誤差約為1．5 m，C1區域中，信標節點的共線度較小，未知節點的定位誤差偏小，相反，C2區域中，信標節點幾乎在同一條直線上，未知節點的定位誤差偏大，同時受邊緣效應的影響，在區域邊緣的平均定位誤差明顯偏大。

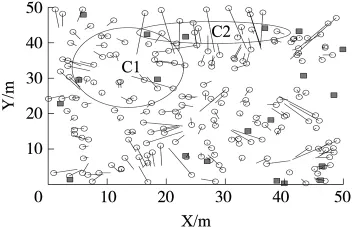
圖7 BBG-EKF定位效果

擴展卡爾曼定位算法的定位精度受迭代次數的影響，迭代次數越多，定位精度越高。圖8是坐標為(5，5)的未知節點分別采用BBG-EKF及BBG-MLE的定位效果，仿真結果表明，BBG-EKF定位算法在迭代15次左右收斂于真實坐標，而BBG-MLE定位算法始終發散。

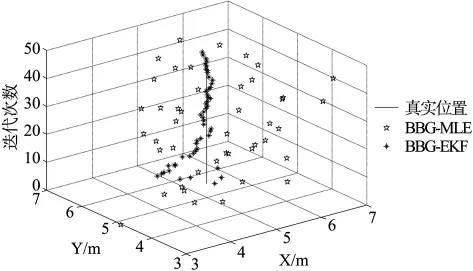
圖8 迭代次數影響

如圖9所示是不同通信半徑下平均定位誤差的比較，其中信標節點占25%。在一定范圍內，通信半徑與網絡連通度成正比，即節點通信半徑越大，平均每個未知節點周圍可通信的節點個數越多。仿真實驗表明:BBG-EKF算法、EKF算法、MLE算法的定位準確度均隨著網絡連通度的增大逐漸提高，BBGMLE雖然存在最優信標選擇機制，但由于沒有擴展卡爾曼濾波過程，當通信半徑大于25 m時平均定位誤差反而增大。與其他三種算法相比BBG-EKF算法穩定性最好，在網絡連通度變化的情況下，都具有較高的定位精度。

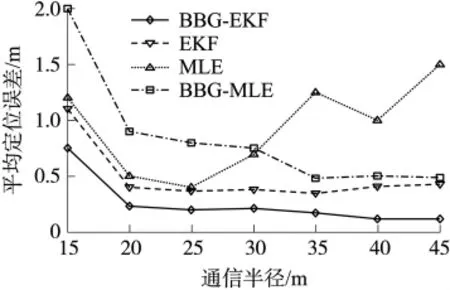
圖9 通信半徑與定位精度的關系

圖10是R=25時信標節點密度對定位誤差的影響。平均定位誤差隨著信標節點密度的增加而降低，在同樣信標節點密度的情況下，BBG-EKF算法具有更好的定位性能，比如在信標密度為15%時，BBG-EKF算法平均定位誤差約為0．37 m，而EKF算法平均定位誤差約為0．52 m，BBG-MLE算法平均定位誤差約為1．42 m，MLE算法平均定位誤差約為0．98 m。另外，BBG-EKF對信標節點密度要求不高，信標節點密度為10%時算法平均定位誤差為0.6 m左右，所以，BBG-EKF不僅具有很好的定位效果，而且適用于信標節點稀疏的環境中。

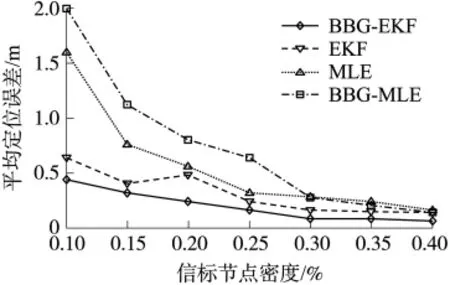
圖10 信標節點密度與定位精度的關系

6 總結

本文采用無線傳感網中的RSSI測距技術，提出一種基于最優信標組的擴展卡爾曼定位算法(BBGEKF)，該算法研究了未知節點與信標節點的距離、信標節點的共線性對定位精度的影響，為合理選擇最優信標節點組進行定位提供了一種方法，最后通過擴展卡爾曼定位技術獲得未知節點的位置信息。仿真實驗表明，本文提出的基于最優信標組的擴展卡爾曼定位算法在沒有增加網絡開銷的情況下，提高了定位精度，在不同通信半徑及信標節點密度的網絡中都表現中良好的性能。

［1］ 孫利民．無線傳感器網絡［M］．北京:清華大學出版社，2005:137－140．

［2］ Capkun S，Hamdi M，Hubaux J P．GPS-Free Positioning in Mobile Ad-Hoc Networks［J］．Cluster Computing，2002，5(2):161 －176．

［3］ Niculescu D，Nath B．Trajectory Based Forwarding and its Applications［C］//Proceedings of the 9th Annual International Conference on Mobile computing and Networking．ACM New York，NY，USA，2003:260－272．

［4］ 劉新華，李方敏．一種分布式的無線傳感器網絡Range-free節點定位算法［J］．傳感技術學報，2008，21(1):154 －157．

［5］ 田增山，羅磊，何維．一種分布式的無線傳感器網絡節點定位算法［J］．傳感技術學報，2009，22(3):387 －390．

［6］ Neal P，Joshua N，Spyros K，et al．Locating the Nodes:Cooperative Localization in Wireless Sensor Networks［J］．IEEE Signal Processing Magazine，2005，22(4):54 －69．

［7］ Mao G，Fidan B，Anderson B．Wireless Sensor Network Localization Techniques［J］．Computer Networks，2007，51(10):2529 －2553．

［8］ 楊東勇，顧東袁，傅曉婕．一種基于RSSI相似度的室內定位算法［J］．傳感技術學報，2009，22(2):264 －268．

［9］ Yi J，Yang S．Multi-Hop Based Monte Carlo Localization for Mobile Sensor Networks［C］//Proceedings of the 9th Annual IEEE Communications Society Conference on Sensor，Mesh and Ad Hoc Communications and Networks，San Diego，CA，2007:162 －171．

［10］ Poqqi C，Mazzini G．Collinearity for Sensor Network Localization［C］//IEEE 58th Vehicular Technology Conference，Ferrara，IT，2003:3040－3044．

［11］ Wang C L，Chiou Y S，Dai Y S．An Adaptive Location Estimator Based Kalman Filtering for Wireless Sensor Networks［C］//IEEE 65th Vehicular Technology Conference，Dublin，IR，2007:864 －868．

［12］ Wang J，Ghosh R K．A Survey on Sensor Localization［J］．Journal of Control Theory and Applications，2010，8(1):2 －11．

［13］吳凌飛，孟慶虎，梁華為．一種基于共線度的無線傳感器網絡定位算法［J］．傳感技術學報，2009，22(5):722 －727．

［14］ Sreenath K，Lewis F L，Popa D O．Simultaneous Adaptive Localization of a Wireless Sensor Network［J］．Mobile Computing and Communications Review，2007，11(2):14 －28．

［15］ Yim J，Park C，Joo J．Extended Kalman Filter for Wireless LAN Based Indoor Positioning［J］．Decision Support Systems，2008，45(4):960－971．