X型鋼管相貫節(jié)點抗彎極限承載力的影響因素分析

廖 賢

(成都大學城鄉(xiāng)建設學院,四川成都 610106)

0 引 言

鋼管結構設計中的一個難點是相貫節(jié)點的設計,由于節(jié)點區(qū)域幾何和材料特性比較復雜,應力集中較為嚴重,且影響因素繁多,破壞形式多樣,因而不能僅依靠力學理論推導來分析節(jié)點的受力狀況.我國《鋼結構設計規(guī)范》(G B50017-2003)[1](以下簡稱《規(guī)范》)10.3.3條規(guī)定:主管和支管均為圓管的直接焊接節(jié)點承載力應按下列規(guī)定計算,其適用范圍為,0.2≤β≤0.2;di/ti≤60,d/t≤100,θ≥30°,60°≤φ≤120°;同時,為保證節(jié)點處主管的強度,支管的軸心力不得大于本條規(guī)定中的承載力設計值.由此可見,《規(guī)范》僅僅給出了鋼管相貫節(jié)點各支管軸向承載力的計算公式,缺乏對節(jié)點抗彎極限承載力規(guī)定.這是由于目前《規(guī)范》中鋼管相貫節(jié)點的承載力計算公式是依據Makino[2]于1996年建立的圓鋼管相貫節(jié)點試驗及有限元分析的數據庫,以及20世紀90年代以來國內高校、設計院和建設單位結合工程實際所做的相貫節(jié)點試驗結果[3].考慮到當時的實際狀況,這些數據庫和試驗結果中鋼管直徑都不大于500 mm,遠遠小于現(xiàn)在許多實際工程中鋼管相貫節(jié)點的尺寸.隨著實際工程中鋼管尺寸的增大,節(jié)點處的彎矩不容忽視,例如某體育場工程,其體育場罩棚采用拱支撐張拉膜結構體系,其中,主體結構采用在節(jié)點處直接相貫連接的鋼管拱架結構,鋼管拱架的總跨度達210 m,其鋼管選用Q345B鋼,采用高頻焊管,該工程中采用了多種形式的大尺寸空間鋼管相貫節(jié)點,節(jié)點種類達28種,其中平面節(jié)點有K型、X型,空間節(jié)點有TT型、X型、X型加單豎桿等.主管規(guī)格分別為Φ920 mm×16 mm和Φ813 mm×12 mm,支管規(guī)格為Φ219 mm×6 mm～Φ914 mm×16 mm.鋼管尺寸如此之大,均已超過鋼結構設計規(guī)范所依據的試驗資料.因此,分析鋼管相貫節(jié)點外抗彎極限承載力的影響因素很有必要.

1 X型鋼管節(jié)點有限元模型的建立

對X型鋼管相貫節(jié)點有限元模型的分析,本文采用shell 181單元三維四節(jié)點彈塑性殼單元.對于普通鋼材,應力應變曲線經歷線彈性階段后,存在較為平緩的屈服平臺,比較接近理想彈塑性,鋼材屈服強度,fy=345 MPa,彈性模量,E=2.06×105MPa,泊松比,v=0.3.使用ANSYS程序中經典的雙線性等向強化選項,材料的屈服準則遵守Von Mises屈服準則及相關的流動法則.在考慮材料非線性時,材料的應力應變曲線按兩折線輸入,材料的強化段采用切線模量為,E=1.03×103MPa,其應力應變曲線如圖1所示.建立有限元模型時不考慮焊縫及殘余應力對節(jié)點極限承載力的影響以簡化模型.

計算模型的邊界條件為:主管左邊界按固定考慮,固定端采用線約束,右邊界按滑動支座考慮;支管邊界為自由端,支管和主管均由相交根部開始外伸3.5倍的管直徑,以消除端部加載條件對節(jié)點區(qū)域的影響.

圖1 材料的應力應變曲線

在模型計算時,影響鋼管節(jié)點抗彎極限承載力的因素取下面兩個:支管直徑(di)與主管直徑(d)比,β=di/d;主管半徑與壁厚(t)比,γ=d/2t.

各因素對鋼管節(jié)點抗彎極限承載力的影響采用單參數分析方法進行[4,5].具體做法是,取一系列模型,變化某一參數,而保持其他參數相同,使得模型抗彎承載力的差異僅由所變化參數的差異引起,從而獲得節(jié)點抗彎承載力隨各參數的變化趨勢.計算時將模型分成兩組,每組考慮一個因素變化對節(jié)點抗彎承載力的影響.

第一組模型考慮,β=di/d,對節(jié)點抗彎極限承載力的影響,結果如表1所示.

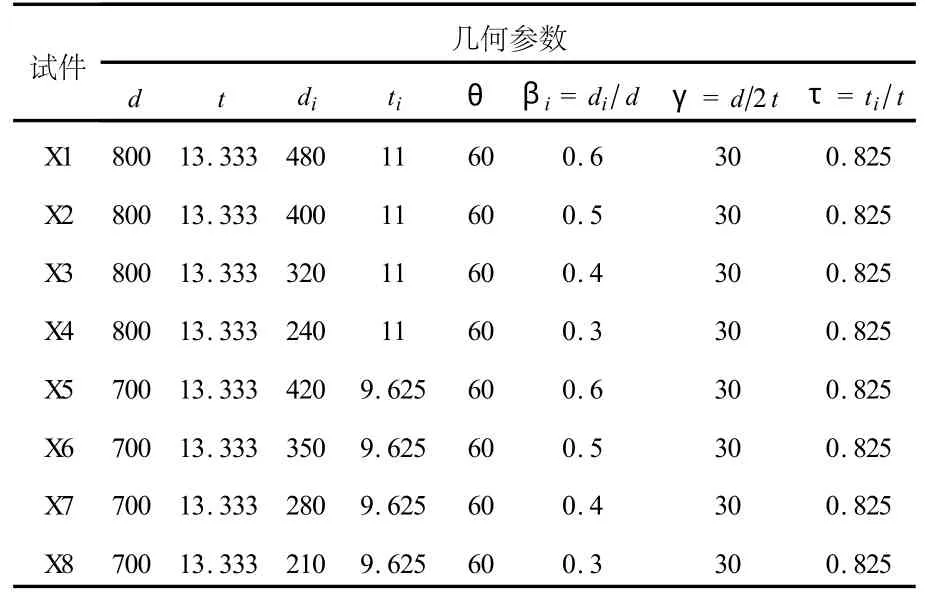
表1 第一組模型計算分析結果

第二組模型考慮,γ=d/2t,對節(jié)點抗彎極限承載力的影響,結果如表2所示.

2 鋼管節(jié)點抗彎極限承載力分析

2.1 承載力的判定

鋼管節(jié)點的破壞模式可能是以強度破壞達到其承載能力的極限狀態(tài),也可能是由于變形太大而不能繼續(xù)承載.因此,對發(fā)生強度破壞的節(jié)點一般是取荷載位移曲線的極值點作為極限承載力,而對變形破壞的節(jié)點則采用變形極限的概念來判定承載力,即取節(jié)點變形達到變形極限時的荷載為極限承載力.對節(jié)點受彎矩荷載的情況,其彎矩轉角曲線一般沒有下降段.故本文采用Yura[6]的方法判定極限彎矩,管節(jié)點受彎矩荷載時,其變形極限取為80fyi/E,其中,fyi為支管屈服強度,E為彈性模量.

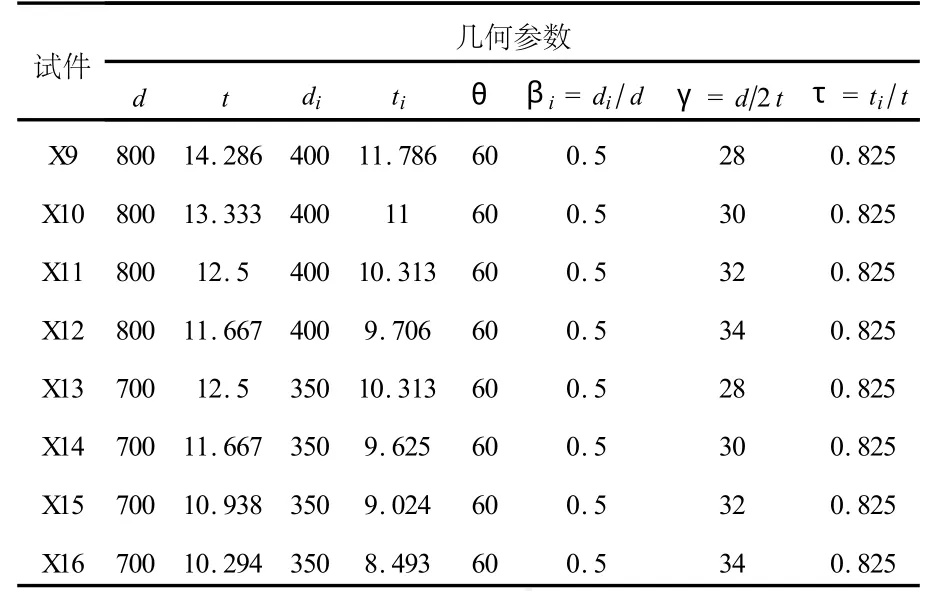
表2 第二組模型計算分析結果

2.2 各因素對鋼管節(jié)點抗彎極限承載力的影響

2.2.1 參數β對抗彎承載力的影響.

圖2是參數β對抗彎極限承載力(Mu)的影響曲線.

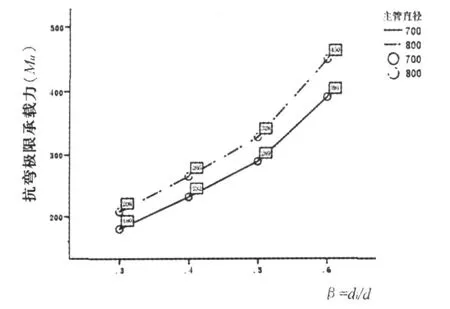
圖2 參數β對抗彎極限承載力(Mu)的影響曲線

從圖2可以看出,鋼管節(jié)點抗彎極限承載力隨參數β的增大而明顯增大.對此,可通過一元非線性回歸來進一步分析節(jié)點抗彎承載力隨β參數變化的規(guī)律.本文比較了3種不同的曲線回歸模型,分別是對數曲線、乘冪曲線和S曲線,通過對曲線回歸模型的擬合效果,模型統(tǒng)計學意義的顯著性和所求參數的t檢驗是否顯著來優(yōu)選,最后確定乘冪曲線擬合的統(tǒng)計意義最顯著.乘冪曲線回歸模型的未知參數分別為691.186和1.082,回歸方程為,

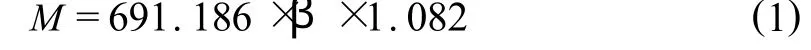
2.2.2 參數γ對抗彎承載力的影響.

圖3是參數γ對抗彎極限承載力Mu的影響曲線.

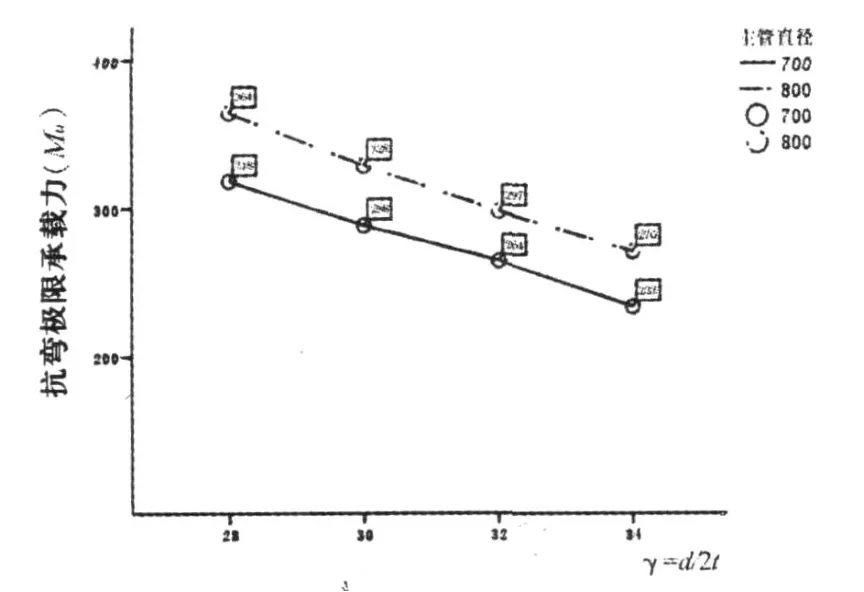
圖3 參數γ對抗彎極限承載力(Mu)的影響曲線

從圖3可以看出,管節(jié)點抗彎承載力隨著γ的增大而明顯的減小.同樣,采用一元非線性回歸來進一步分析節(jié)點受彎承載力隨γ參數的變化規(guī)律.同樣,本文比較了3種不同的曲線回歸模型,分別是乘冪曲線、S曲線和growth曲線.通過對曲線模型的擬合效果,模型統(tǒng)計學意義的顯著性和所求參數的 t檢驗是否顯著的優(yōu)選,最后確定growth曲線擬合效果最好,growth回歸模型的未知參數分別為691.186和1.082,回歸方程為,

3 結 論

通過分析X型鋼管相貫節(jié)點考慮附加彎矩后的極限承載力,我們得出以下結論:在考慮幾何非線性和材料非線性的情況下,通過單參數分析和力學原理推導分析了主管直徑比,β=di/d,主管直徑與壁厚比,γ=d/2t,對 X型鋼管節(jié)點的抗彎極限承載力的影響,并用數理統(tǒng)計的方法證明,鋼管節(jié)點受彎承載力隨參數β的增加近于乘冪曲線的增長,隨參數γ的增加近于growth曲線的增長.需要說明的是,本文只就參數β和γ分析了16個數值模型,鑒于影響鋼管節(jié)點抗彎極限承載力的因素眾多,對它的分析尚需做更多影響因素和更多模型的進一步的分析.

[1]中華人民共和國建設部.G B50017-2003鋼結構設計規(guī)范[M].北京:中國計劃出版社,2003.

[2]Makino Y,Kurobane Y,Ochi K,et al.Database of Test and Numerical Analysis Results for Unstiffened Tubular Joints[M].New Y ork:Elsevier Inc,1996.

[3]鋼結構設計規(guī)范編制組.鋼結構設計規(guī)范專題指南[M].北京:中國計劃出版社,2003.

[4]廖賢.大尺寸空間KK型圓鋼管相貫節(jié)點的極限承載力分析[D].重慶:重慶大學,2009.

[5]邱國志.圓鋼管X型相貫節(jié)點剛度及其對結構整體性能的影響[D].上海:上海交通大學,2008.

[6]Yura J A,Zettlemoyer N,Edwards I F.Ultimate Capacity Equations for Tubular Joints[C]//12th Annual Offshore Technology Conference.Houston:OTC Press,1980.