原子熒光法檢驗小白菜中砷制樣均勻性不確定度的評定*

占永革，龔劍，黃湘燕，陳颯，李志梅，王偉彤

1(廣州大學環境檢測中心，廣東廣州，510006)2(中山市供水有限公司水質檢測中心，廣東 中山，528403)

食品樣品進入實驗室后(即實驗室樣品)的檢測活動包括制樣、樣品轉化、測量等主要過程。食品檢驗的制樣常指按技術規范將進入實驗室的樣品通過取可食部分、縮分、清洗與去除清洗水分、搗碎或勻漿等操作處理使樣品成為轉化前的狀態，一般不包括按檢測方法對樣品進行諸如消化、提取、純化等操作將樣品轉化成可直接測量之狀態的轉化過程［1－2］。用于測量的樣品一般是經過四分法［2－4］縮分后到最后的樣品，其與縮分途中舍去的樣品之一致性直接影響著實驗室樣品檢驗結果的可靠性，特別是對于那些物質含量隨可食部位不同而不同［5－9］的食品樣品，制樣均勻性將是影響實驗室樣品檢驗結果準確度的主要因素之一，也是實驗室樣品測量不確定度的主要來源之一。但從已發表的食品檢驗不確定度評估文獻看，人們多關注樣品轉化及其以后的環節，這可能源于檢測方法多從樣品轉化步驟開始描述［10］，而對制樣環節的均勻性影響關注得較少。本文嘗試以原子熒光法檢驗非均勻性小白菜中砷為例評定了其制樣均勻性不確定度，其結果和方法對同行具有一定的參考意義。

1 制樣過程

1.1 縮分與取樣

第一次縮分與取樣:去除進入實驗室約6 kg小白菜樣品的泥土和腐葉，以自然蔸為單位按矩形平鋪于清潔的無色聚乙烯塑料薄膜上，采取對角線分割法將位于對角線上下區域的樣品取出并混合均勻后記為m1，將對角線左右區域的樣品混合均勻后記為A;將全部m1樣品的菜瓣一一掰下混合均勻后以矩形平鋪于薄膜上，隨機抽取矩形面上下左右各方位的菜瓣約125 g代表第一次縮分舍去的樣品;留下的A樣品用于第二次縮分。

第二次縮分與取樣:將全部A樣品的菜瓣一一掰下混合均勻后以矩形平鋪于薄膜上，按對角線分割法將位于對角線上下區域的樣品取出并混合均勻后記為m2，將對角線左右區域的樣品混合均勻后記為B;將全部m2樣品以矩形平鋪于薄膜上，隨機抽取矩形面上下左右各方位的菜瓣約125g代表第二次縮分舍去的樣品;留下的B樣品用于第三次縮分。

第三次縮分與取樣:將全部B樣品以矩形平鋪于薄膜上，按對角線分割法將位于對角線上下區域的樣品取出并混合均勻后記為m3，將對角線左右區域的樣品混合均勻后記為C;將全部m3樣品以矩形平鋪于薄膜上，隨機抽取矩形面上下左右各方位的菜瓣約125 g代表第三次縮分舍去的樣品;留下的C樣品用于第四次縮分。

第四次縮分與取樣:將全部C樣品以矩形平鋪于薄膜上，按對角線分割法將位于對角線上下區域的樣品取出并混合均勻后記為m4，將對角線左右區域的樣品混合均勻后記為D;將全部m4樣品以矩形平鋪于薄膜上，隨機抽取矩形面上下左右各方位的菜瓣約125 g代表第四次縮分舍去的樣品;將留下的D樣品均分3份(約125 g)分別用于檢測(記為m5)、留樣和復檢。

1.2 樣品處理

依次用自來水和純凈水沖洗菜瓣樣品m1、m2、m3、m4、m5，用干凈紗布輕輕擦去菜瓣上的水分，用不銹鋼剪刀分別將各樣品剪碎于組織搗碎機中搗碎3 min成勻漿，轉移至高密度聚乙烯塑料瓶中。

分別從 m1、m2、m3、m4、m5勻漿樣品中平行稱取3份10 g左右的子樣n1、n2、n3進行檢測。

2 檢測方法及結果

2.1 檢測方法

檢測方法:GB/T5009.11－2003食品中總砷和無機砷的測定。總砷的測定，氫化物原子熒光光度法，樣品處理、檢測過程、測量條件和結果計算均按方法規程進行;樣品采用濕法消解。

2.2 檢測結果

As的檢測結果見表1。

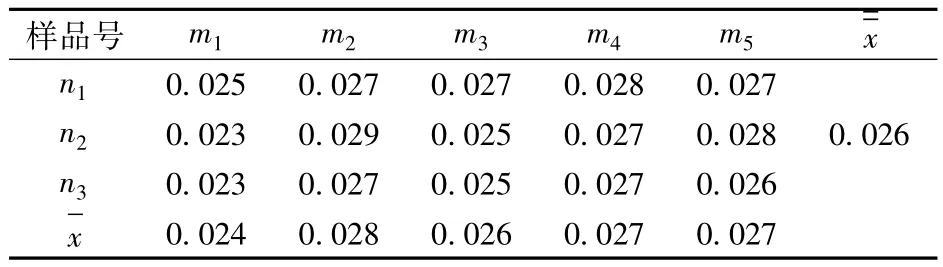
表1 樣品均勻性檢測結果 mg/kg

3 均勻性不確定度的評估

3.1 均勻性檢驗及標準差

采用單因子方差分析進行樣品均勻性檢驗［11－13］。

由表1可知，樣品數(即樣品間樣品數)m=5，每個樣品在重復條件下的檢測次數(即樣品內樣品數)n=3，總檢測次數N=15，樣品間自由度f1=m－1=5－1=4，樣品內自由度f2=N－m=15－5=10。

(1)樣品間平方和SS1:

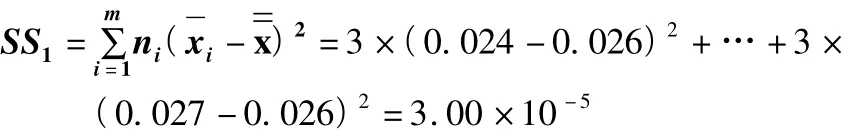
(2)樣品間均方MS1:

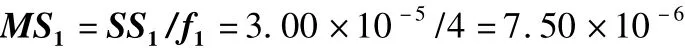
(3)樣品內平方和SS2:

(4)樣品內均方MS2:

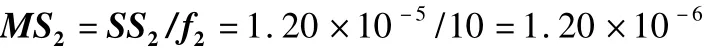
(5)統計量F的計算:

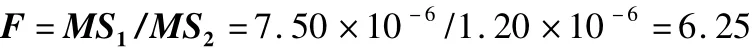
(6)統計量比較:

查得 F0.05，(4，10)=3.48，因 F=6.25 ＞ F0.05，(4，10)=3.48，表明樣品間有顯著性差異，樣品間含量不均勻。

(7)樣品間不均勻性標準差SS:

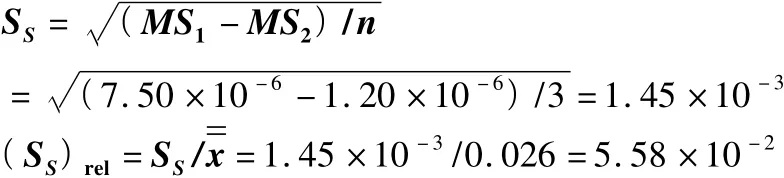
3.2 偏倚檢驗

日常用于檢測的樣品實際上僅是m5，其均值與均勻性實驗樣品的總均值之間是否存在差異需進行檢驗。

計算表1中樣品m53次檢測數據的標準差S1=1.00×10－3;表1中的總標準差 S2=1.75 ×10－3;合并自由度 f=3+15－2=16;查得統計量臨界值t0.05，16=2.12。

(1)合并標準差S的計算:

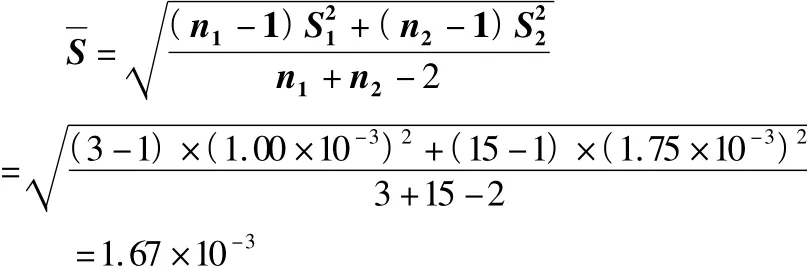
(2)統計量t的計算:

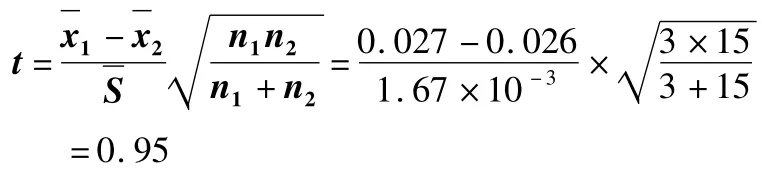
(3)統計量比較:

因 t=0.95 ＜ t0.05，16=2.12，故 ms之均值與總均值的偏倚為零。

3.3 均勻性不確定度urel的計算

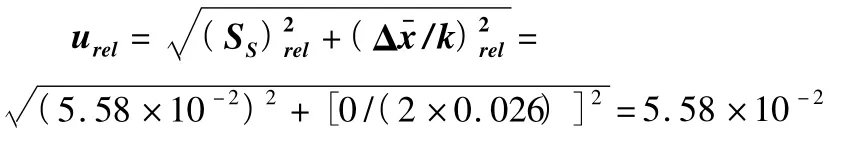
4 討論

(1)本例制樣均勻性相對不確定度為5.58×10－2，此量級與常占主要地位的曲線擬合濃度的不確定度、回收率及方法偏差不確定度的量級相當。這表明，制樣均勻性引入的不確定度是檢驗非均勻性食品樣品測量不確定度的主要來源之一，在評估非均勻性食品樣品的測量不確定度時不可忽視制樣環節的影響。

(2)縮分是一個對實驗室樣品進行取舍的操作，日常檢測均假定按技術規范縮分到最后的那部分樣品對于實驗室樣品而言是均勻的，是可以代表整個實驗室樣品的。但實際上縮分途中取舍的樣品之間是存在差異的特別是對非均勻性樣品，由于制樣均勻性是對整個實驗室樣品而言，故制樣均勻性樣品的采集應該包括縮分途中所舍去的樣品。

(3)有將制樣均勻性包含于測量重復性的處理方法［14－16］。筆者認為，如果僅是從縮分到最后的那一份樣品中分取子樣，其數據只能反映該份樣品內的綜合情況，難以反映實驗室樣品的制樣均勻性。一般縮分到最后的那份樣品量不多，容易搗碎均勻，故子樣間的數據更多反映的是重復性而非均勻性。

(4)在每個縮分樣品中(母樣間)分取子樣的做法與所用統計方法有關，若采用單因子方差分析法則需要有母樣和子樣，母樣反映樣品間的均勻狀態，子樣反映樣品內的均勻狀態，故子樣至少應從母樣中分取2個以上，僅取一個子樣并對其重復測量例如對一個樣品進行n次比色，這只能反映測量(比色)這一環節的重復性狀態，不能反映樣品內的均勻狀態。

(5)一般用于樣品均勻性檢驗的統計規則有單因子方差分析法［11－13］、均值分析法［17］和極差分析法［18］，不均勻性樣品標準差(不確定度)的算法除了有以上各自配套的算法外，還有采用貝塞爾法［19］。同一組實驗數據，采用不同的檢驗規則可能得出相反的檢驗結論，不同的標準差算法會使計算結果存在差異［20］，本例分別采用上述規則及其算法也出現了這種情況。筆者建議采用國標推薦的單因子方差分析法及其配套的標準差算法，一是因為標準物質生產者的資質統一由中國合格評定國家認可委員會認定認可，而認可委等同采用了該項國家標準［11］，讓這項標準統一到整個量值溯源過程，可保證數據的可比性;二是因為樣品間均勻性的檢測結果并不是獨立的，實際上疊加了樣品內的不均勻性和檢測過程的隨機效應，而單因子方差分析的標準差算式可以扣除樣品內不均勻性及其隨機效應，相當于扣除了樣品空白，使得制樣均勻性不確定度評估結果的可靠性更高。

(6)一些技術規范［2－4］描述將蔬菜可食部分先截斷后縮分。筆者認為，對于小白菜這類梗葉一體且梗葉含量不同的蔬菜，不宜將梗葉先截斷后縮分，而應以菜瓣為單位保持梗葉一體進行縮分，因為將梗葉截斷后再混合難以保持蔬菜梗葉的自然分布規律，容易出現某方位的梗葉分布不均而使各方位樣品間的含量不等人為造成制樣不均勻。

(7)評估制樣均勻性不確定度需增加較多的檢測樣品，增加了日常不確定度評估的工作量。四分法的取樣規則是留用縮分到最后的那部分樣品，因而產生縮分途中舍去的樣品與最后留用的樣品是否一致的問題，特別是對于非均勻性樣品。如果用于檢測的樣品在縮分途中就開始取樣，包括各次縮分中舍去的樣品，則該混合樣品及其檢測結果可基本保持實驗室樣品的整體屬性，可望忽略制樣均勻性的影響及其造成的偏倚而省去對制樣均勻性不確定度分量的評估。

［1］ GB/T5009.11－2003.食品中總砷和無機砷的測定［S］．

［2］ GB/T27404－2008.實驗室質量控制規范 食品理化檢測 附錄E［S］．

［3］ NY/T 398－2000.農、畜、水產品污染監測技術規范［S］．

［4］ 中國農業科學院農業質量標準與檢測技術研究所．農產品質量安全檢測手冊果蔬及制品卷［M］．北京:中國標準出版社，2008:32－33.

［5］ 周箏．成都市某蔬菜基地蔬菜中重金屬含量分布研究［J］．成都電子機械高等專科學校學報，2007(1):19－21，40.

［6］ 許金蓉，王清章．蓮中總酚含量與分布研究［J］．安徽農業科學，2010，38(25):13 680－13 681.

［7］ 任初杰，石勇，王承明．包菜中重金屬的空間分布研究［EB/OL］．北京:教育部科技發展中心，中國科技論文在線，http://www．paper．edu．cn/index．php/default/releasepaper/content/200706－84.

［8］ 劉丹赤，邵長明．魚體內重金屬含量測定及其分布狀況的研究［J］．中國測試技術，2007，33(4):121－122，132.

［9］ 汪 軍，王盛良，李家奎，等．南京地區市售雞蛋的含硒量調查［J］．食品科學，2000，21(3):44－45.

［10］ GB/T 5009.食品衛生檢驗方法 理化部分［S］．

［11］ CNAS－GL29標準物質/標準樣品定值的一般原則和統計方法［EB/OL］．北京:中國合格評定國家認可委員會，2010.http://219.238.178.51/bx90/sites/cnas/extra/col23/1295319708.pdf．

［12］ GB/T15000.3－2008.標準樣品工作導則(3)標準樣品 定值的一般原則和統計方法［S］．

［13］ CNAS—GL03能力驗證樣品均勻性和穩定性評價指南［EB/OL］．北京:中國合格評定國家認可委員會，2006. http://219.238.178.51/bx90/sites/cnas/extra/col23/1153814696.pdf．

［14］ 陳世山，高建國，劉夢．氣相色譜一質譜聯用法測定水果中環氧七氯殘留量的不確定度評定［J］．化學分析計量，2005，14(2):8 －11.

［15］ 甘合智．氣相色譜法測定腐乳中脫氫乙酸的測量不確定度評定［J］．化學分析計量，2007，16(5):10－13.

［16］ 楊振宇，郭德華．食品中苯甲酸、山梨酸含量測量不確定度的評估［J］．化學分析汁量，2003，12(3):3－6.

［17］ 中華人民共和國國家發展和改革委員會YB/T 4143－2006.檢驗研制標準樣品所用材料均勻性的規則［S］．北京:冶金工業出版社，2007.

［18］ 鄧勃．數理統計方法在分析測試中的應用［M］．北京:化學工業出版社，1984:226－228.

［19］ 馬振棟，王鳳池，郝冬生．高效液相色譜柱后衍生法測定黃曲霉毒素的不確定度評定［J］．計量學報，2002，23(3):229 －232，240.

［20］ 張勇，劉英，臧慕文，等．光譜分析用標準物質/樣品均勻性不同檢驗規則比較及其不確定度評定［J］．分析試驗室，2011，30(1):76 －78.