液壓缸穩定性設計的模糊可靠性計算

龔相超，胡百鳴

（武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北武漢，430065）

有關液壓缸臨界載荷的計算方法很多，但不同的計算方法和計算模型結果差別很大[1]，原因是液壓缸所受載荷的工作階段及環境因素的不同，致使液壓缸的失穩因素具有某種不確定性，即模糊性和隨機性。常規液壓缸穩定性計算采用的是安全系數法，該法較大程度上依賴于設計者的經驗，因而不能充分反映實際存在的諸多不確定性因素的影響，為此，本文采用模糊可靠性方法來計算液壓缸的穩定性。

1 模糊可靠度計算原理

設液壓缸工作壓力P和臨界壓力Pcr分別為論域U，V上的模糊子集S、R，故P∈U，Pcr∈V，且用數s、r來表述，s∈[0，1]，r∈[0，1]，s、r分別為S、R的隸屬度。S、R的隸屬函數分別為fs（P）、fr（Pcr）。模糊子集R中每個元素Pcr都可以作為穩定性判據，因而將傳統設計中的單一判據擴大為判據空間，在此基礎上進行液壓缸穩定性可靠度的計算，以此增大與實際情形相符的概率[2]。

設判據實空間Ω，對任意一個作為判據Pcr（Pcr∈Ω）都指定一個數μr∈[0，1]，即判據Pcr對模糊判據集（臨界壓力模糊子集R）的隸屬度，考慮到設計的安全因素，其隸屬度函數采用連續偏小型隸屬度函數。液壓缸的軸向壓力P可按隨機變量來設計，常見的分布有正態分布、威布爾分布等，一般根據實際工況來確定，本文計算采用正態分布。根據模糊等效隨機原理，將復雜的模糊不確定性等效為隨機不確定性[3]，得到工作壓力概率密度分布函數與液壓缸臨界壓力Pcr的隸屬函數組合，液壓缸穩定性模糊可靠度可采用概率密度函數聯合積分法積分得到，也可采用功能密度函數積分法得到[4]。

2 臨界壓力隸屬函數

表1 臨界載荷計算值Pcr、實測值Pcr1及相對誤差δTable 1 Theoretical and experimental critical load values

傳統液壓缸穩定性設計多采用歐拉公式和拉金公式[5]，且將液壓缸視為理想的等截面直桿，截面慣性矩取活塞桿與缸筒中較小者。研究表明，該法所得臨界壓力值趨于保守，作為判據的可信度為1。采用文獻[6]試驗數據，臨界載荷歐拉計算值、實測值及相對誤差如表1所示。從表1中可以看出，所有臨界載荷的實測值均較計算值大，最大相對誤差為30.7%，最小相對誤差為1.3%，平均相對誤差為19.2%。因此臨界載荷的隸屬度函數采用降半階正態分布[7]，如圖1所示。臨界壓力為正態型模糊變量，其隸屬度函數可表示為

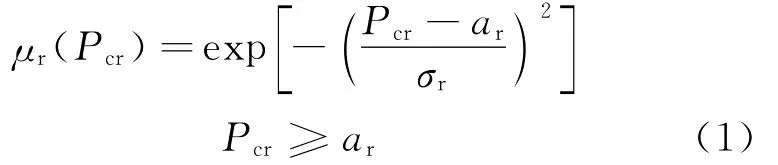
式中：μr（Pcr）為模糊臨界壓力的隸屬度函數；Pcr為模糊臨界壓力；ar為等截面歐拉公式計算值；σr為模糊臨界壓力的標準差。

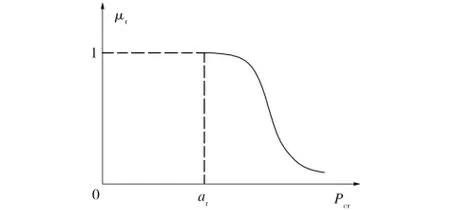
圖1 臨界載荷隸屬度函數Fig.1 Membership grade function of critical load

σr是反映液壓缸真實臨界壓力合理取值的重要參數，將液壓缸臨界壓力這一模糊變量等效為隨機變量，則模糊臨界壓力等效概率密度函數為

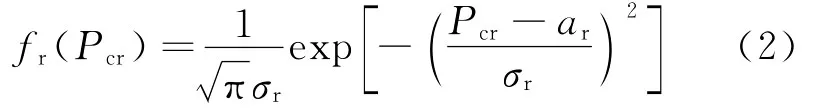
3 模糊可靠度

鑒于現場工況較為復雜，液壓缸所受荷載具有很大的隨機性，故將本文液壓缸隨機載荷視為正態分布形式，其概率密度函數為

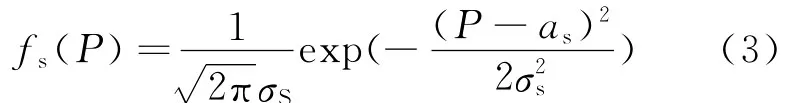
式中：P為隨機載荷；as為隨機載荷均值；σs為隨機載荷標準差。

為了使計算結果盡可能符合實際情況，隨機載荷標準差σs應根據實際統計數據確定。基于現場諸多不確定性因素，as的離散性很大，故取

對于已知臨界壓力和工作載荷概率密度的情形，可采用概率密度函數聯合積分法得到可靠度[4]，概率密度函數聯合積分原理如圖2所示。代入載荷和臨界壓力的概率密度函數積分后可得液壓缸穩定性可靠度R。

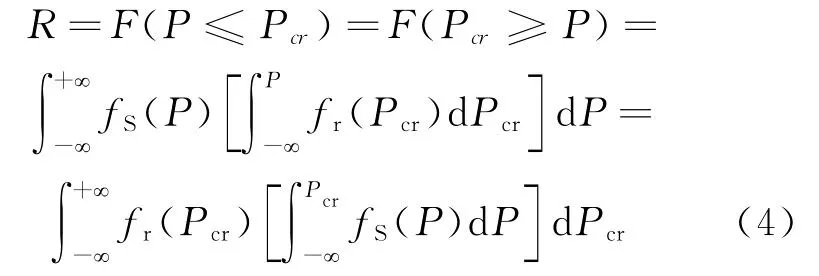
若式（4）積分得不到原函數，則可用數值積分計算出可靠度。由于本文液壓缸的臨界壓力和工作載荷均為正態分布，且二者為相互獨立的隨機變量，所以采用功能密度函數積分法[3]得到。定義隨機變量Z＝Pcr－P仍服從正態分布N（aZ，σZ），其中；可靠性指數則可靠度符合標準正態分布。

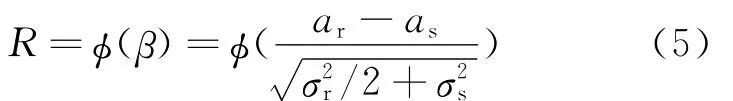
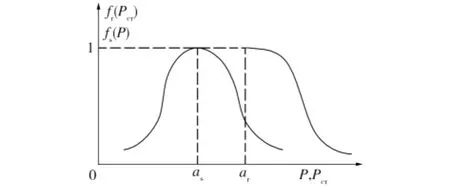
圖2 概率密度函數聯合積分Fig.2 Joint probability density function integral

液壓缸可靠度可查標準正態概率積分表得到。可見用式（5）來計算穩定性可靠度簡單易行。

4 計算實例

沿用文獻[1]表2中的第5號液壓缸，等截面直桿臨界壓力計算值和試驗實測值分別為126.27 k N和153.46 k N，相對誤差為17.7%，將數值代入式（1），且σr＝0.192ar，可得臨界壓力的隸屬度函數和等效概率密度函數分別為

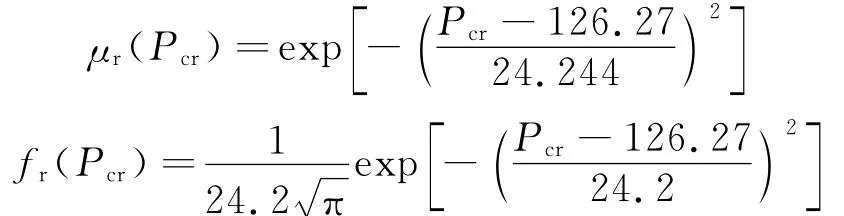
鑒于液壓缸工況環境復雜，取安全系數為k＝2，as＝ar／k，且令σs＝0.2as

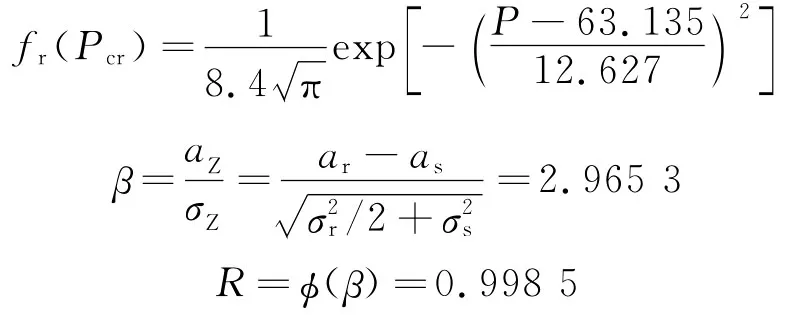
對于工況特別復雜的情形，可取k＝2.5，令σs＝0.3as，則β＝3.235 0，R＝0.999 4。考慮到液壓缸的臨界載荷受到液壓油、導向長度、約束等諸多因素的影響，參考表1中數據，宜取σr＝0.2ar和σs＝0.2as。

5 結語

本液壓缸穩定性可靠度計算方法為復雜環境和載荷及特殊工況下的設計提供了一條新思路，可以降低傳統液壓缸設計中對設計者經驗的依賴性。本文中的幾個重要參數的選取僅參考了表1中的1組實驗數據，要想獲得與實際情況吻合的理想參數值，尚需進行大量的試驗數據統計分析。本文各個參數和概率的計算采用了MATLAB軟件編程，MATLAB提供了豐富的概率統計函數，使得計算程序異常簡潔。

[1] 龔相超，胡百鳴.基于能量原理的液壓缸靜力穩定性的計算[J].礦山機械，2011（3）：109－112.

[2] 郭書祥，呂震宙.概率模型含模糊分布參數時模糊失效概率計算方法[J].機械強度，2003，25（5）：527－529.

[3] 董玉革.機械模糊可靠性設計[M].北京：機械工業出版社，2000：16－19.

[4] 劉揚松，徐小兵.機械模糊可靠性理論與應用[M].武漢：中國地質大學出版社，2002：29－31，79－81.

[5] 王益群，高殿榮.液壓工程師技術手冊[M].北京：化學工業出版社，2010：159－160.

[6] 郭應龍.液壓缸穩定性分析[J].武漢水力電力學院學報，1988（2）：23－29.

[7] 蔣澤軍.模糊數學教程[M].北京：國防工業出版社，2004：27－30.

[8] 楊雄.井架實腹式軸心壓桿穩定性計算新方法[J].石油機械，2006，34（8）：28－29.