瀝青混合料損傷蠕變模型試驗研究

曾國偉，楊新華，尹安毅，磨季云

（1.武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北 武漢，430065；2.華中科技大學土木與力學學院，湖北 武漢，430074）

瀝青混合料是應用廣泛的一種路面工程材料，在承受載荷以前其內部已存在許多微裂紋和微缺陷。在損傷本構模型的建立過程中，物體內存在微缺陷可以理解為連續的變量場（損傷場）［1］，而損傷會導致材料失效，因此瀝青混合料的損傷分析具有重要意義。

目前國內針對瀝青混合料損傷分析的研究較少。張久鵬等［2］對Burgers模型中串聯黏壺進行了改進，引入應變硬化變量和損傷軟化變量，建立了基于應變硬化理論的瀝青混合料損傷蠕變模型，其模型參數過于復雜。王后裕等［3］分析了瀝青混合料加載時的固結效應和卸載時的永久變形等流變學特征。Ye等［4］在大量瀝青砂單軸蠕變實驗的基礎上，對Burgers模型做了進一步的研究，通過構建黏塑性體得到了能適應單軸實驗條件、反映瀝青砂整個蠕變特征的非線性蠕變模型，模型物理意義明確，但未考慮損傷的影響。

本文在瀝青混合料單軸蠕變實驗的基礎上，考慮三元件模型參數隨時間劣化的特性，通過耦合一個連續性蠕變損傷因子，以簡單的元件組合得到一種能適應單軸載荷條件、完整反映瀝青混合料整個蠕變特征的黏彈性損傷蠕變模型，并對瀝青混合料蠕變過程中的損傷演化進行定量分析。

1 蠕變實驗

1.1 實驗原料

實驗瀝青為AH－70重交通道路石油瀝青，其25℃針入度為69（0.1mm），15℃延度大于200 cm，軟化點為47℃。瀝青混合料試樣采用AC－13C標準級配，瀝青摻量為5.1%，骨料級配比例如表1所示［5］。采取一次壓縮成型方法，將混合料制成直徑和高均為100mm的圓柱體試樣。

表1 瀝青混合料骨料級配Table1 Aggregate gradation of asphalt mixture

1.2 實驗方案

25℃環境溫度下，分別取保載應力為0.28、0.71、1.41MPa進行蠕變實驗。實驗前對試樣預加載0.1MPa，停留時間5min，以消除機械誤差影響，并在要求溫度下保持60min以上，實驗時試樣兩端各墊一張用于減少端面摩擦的薄膜紙。整個實驗在帶有環境溫度箱和反向加載裝置的電子萬能實驗機上進行。相同實驗重復進行3次，結果取平均值，記錄蠕變曲線和蠕變破壞時間。

1.3 實驗結果及分析

圖1為25℃時瀝青混合料試樣在3種應力水平下的蠕變曲線，為便于觀察，蠕變應變取絕對值。從圖1中可以看出，瀝青混合料在較大荷載作用下的蠕變可分為遷移期、穩定期和破壞期三個階段：遷移期，變形迅速增大，但應變速率隨時間的延長逐漸減小；穩定期，應變穩定增大，但應變速率基本保持不變；破壞期，應變、應變速率隨時間延長迅速增大直至試樣破壞。而較小荷載作用下瀝青混合料的蠕變則可能只有遷移期和穩定期兩個階段，呈現固結效應［3］。

圖1 不同應力水平下瀝青混合料蠕變實驗曲線Fig.1 Experimental curves of asphalt mixture at different stress levels

2 蠕變損傷模型的建立

2.1 黏彈性蠕變模型

模型元件可以較好地反映材料的蠕變特性。本文以三參量模型［6］為基礎，建立瀝青混合料的蠕變模型。三參量模型包含有一個Kelvin模型和一個彈簧元件，模型的彈性參數E1、E2和黏彈性參數η2如圖2所示。

圖2 三元件黏彈性損傷模型Fig.2 H－K viscoelastic damage model

三元件模型的本構方程為［6］

對式（2）積分，并引入邊界條件t＝0時，模型顯示瞬時彈性，即

2.2 考慮損傷的蠕變模型

由于瀝青混合料內部蠕變流動，從而導致材料內部產生微裂紋及微空洞，并在時間的推移下不斷發展，致使瀝青混合料的彈性模量和強度逐漸降低，因此本文提出的蠕變模型中各元件的系數在蠕變過程中隨損傷的增加不斷衰減。采用損傷力學方法研究瀝青混合料的蠕變特性，首先需要選擇合適的損傷變量。對于單軸壓縮應力狀態，Kachanov蠕變損傷律為［1］

Lemaitre［7］提出應變等效假設，認為受損材料的變形行為可以只通過有效應力來體現，任何損傷材料的本構關系與無損時的形式相同，只要將其中的名義應力替換為有效應力即可。將式（7）中的損傷代入到式（8）中，再代入式（4），即可得瀝青混合料考慮損傷時的蠕變本構模型方程：

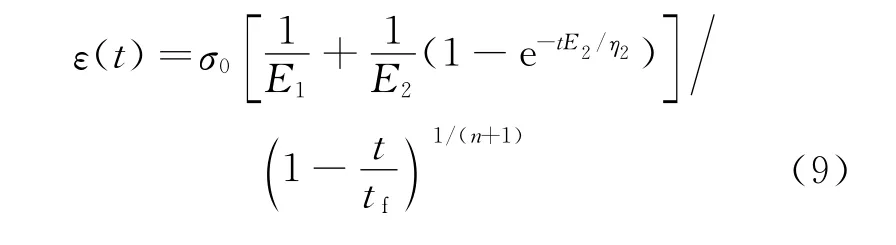
3 模型計算結果與分析

損傷蠕變模型中的各元件參數（E1、E2、η2、tf和n）可通過非線性擬合程序確定。根據非線性最小二乘法原理，編制瀝青混合料實驗數據的擬合程序，在程序中輸入合適的模型參數初始值，通過非線性循環反演即可求得本文模型各個參數的值。表2列出了25℃時不同應力水平下模型參數的擬合結果。由表2中可見，相關系數都在0.99以上，可以判定非線性程序具有相當高的擬合精度。

表2 25℃時不同應力水平下蠕變損傷模型參數值Table2 Creep damage model parameter values at 25℃and different loading stresses

圖3所示為瀝青混合料在不同應力水平下的蠕變損傷模型計算值與實驗結果的對比圖。由圖3中可見，由本文模型計算得到的軸向蠕變預測曲線與實驗值非常接近。當應力水平為0.28 MPa時，本文模型預測曲線能反映瀝青混合料的遷移期蠕變和穩定期蠕變；當應力水平為0.71 MPa和1.41MPa時，本文模型預測曲線不僅能反映瀝青混合料的初期衰減蠕變和穩態蠕變階段的蠕變應變，還能很好地反映加速蠕變階段的蠕變應變，表明本文提出的模型是有效的。

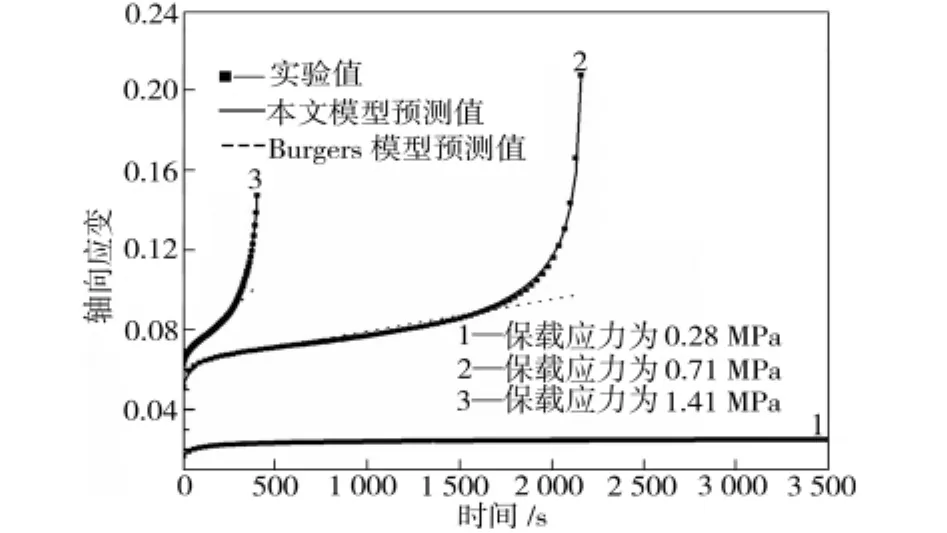
圖3 不同應力水平下蠕變實驗結果與模型預測值Fig.3 Comparsion of experiment and models curves at different stress levels

目前采用較多的Burgers模型能較好的反映遷移期與穩定期階段，但無法描述破壞期階段。本文模型中值得關注的是表征破壞臨界時間的參數tf。tf值越大，瀝青混合料進入破壞期的時間越長。而在低應力水平下，tf值為負值，表明此時已無法進入破壞期階段，瀝青混合料的蠕變呈現典型的固結效應。

圖4為不同應力水平下瀝青混合料的蠕變損傷演化曲線圖。由圖4中可以看出，在較高應力水平（0.71MPa）下，開始時由于孔隙閉合，損傷的發展較為緩慢，接近破壞時，骨料與瀝青瑪蹄脂界面逐漸剝離，損傷會快速發展；而低應力水平下，損傷發展趨向一個較小的固定值，這與瀝青混合料固結效應理論相吻合。

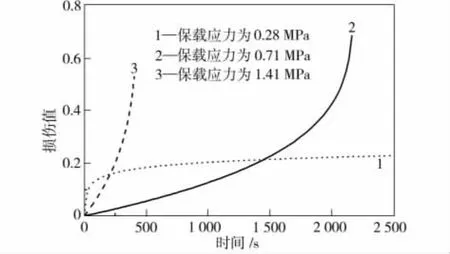
圖4 不同應力水平試樣的損傷蠕變曲線Fig.4 Creep damage curves at different stress levels

4 結語

依照Kachanov蠕變損傷律建立與流變臨界時間相關的損傷因子，將損傷因子耦合到黏彈性三元件蠕變模型中，得到改進后的蠕變損傷模型，可較好地反映瀝青混合料蠕變過程的3個階段。該模型預測值與試驗結果非常接近，與常用的黏彈性模型對比，更好地反映了加速蠕變的非線性特征，表明該模型用于損傷分析是有效的。

［1］余壽文.損傷力學［M］.北京：清華大學出版社，1997：47－49.

［2］張久鵬，黃曉明.瀝青混合料永久變形的彈黏塑－損傷力學模型［J］.東南大學學報：自然科學版，2010，40（1）：185－189.

［3］王后裕，朱可善，言志信.瀝青混合料蠕變柔量的一種實用模型及其應用［J］.固體力學學報，2002，23（2）：232－236.

［4］Ye Yong，Yang Xinhua，Chen Chuanyao.Experimental researches on visco－elastoplastic constitutive model of asphalt masti［J］.Construction and Building Materials，2009，23（10）：3161－3165.

［5］葉永.瀝青混合料黏彈塑性本構模型的實驗研究［D］.武漢：華中科技大學，2009.

［6］楊挺青.黏彈性力學［M］.武漢：華中理工大學出版社，1990：15－18.

［7］Lemaitre J.A course on damage mechanics［M］.Berlin：Springer，1992：22－34.