巧解競賽題的一種方法
——“補償法”
肖建華
(太倉高級中學 江蘇 太倉 215400)
在物理學的學習過程中,當常規方法對復雜的物理問題無能為力時,一些特殊的方法往往能發揮其獨特的威力,將復雜的物理問題由難變易,由繁變簡;補償法就是一種有效可行的方法.所謂補償法就是在與原問題和物理規律不相違背的前提下,適當補充一些物理條件,從而求解物理問題的方法.本文結合具體題例,簡要總結了使用補償法求解物理競賽中萬有引力、質心、感應電動勢等基本物理量的問題,以及復雜的運動問題.
1 在力學中的應用
在力學中常常會遇到這一類問題:一個幾何對稱的物體中間被挖掉一部分.
1.1 用補償法求萬有引力
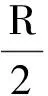
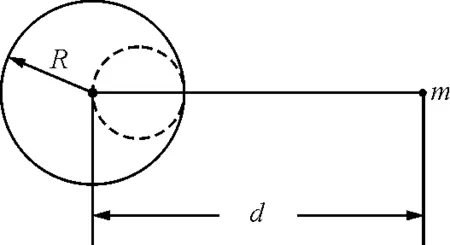
圖1
解析:萬有引力公式適用于真空中的質點,均勻球體可以等效成質量集中于球心的質點.本問題是求不規則的物體和質點之間的萬有引力,沒有現成的公式可以用,需要變換思維角度.假設把用同樣密度的均勻分布的物質填滿空穴,這樣就形成了完整的均勻球體.完整的球體跟質點m之間的引力為
F=F1+F2
其中F1表示剩余部分對m的吸引力,所以
F1=F-F2=
1.2 用補償法求質心
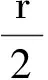
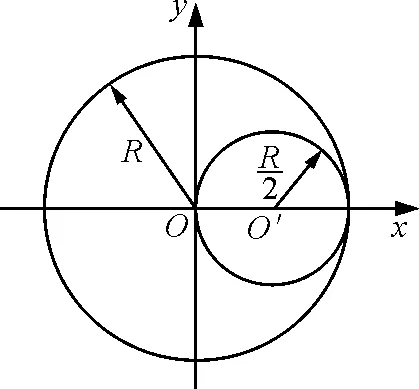
圖2
解析:由于圓盤不是幾何對稱,一般都采取積分法求質心,但計算相當繁復.如果用補償法處理,那就是在挖去的部分先填上密度和薄圓盤相同的物質Δm.補上Δm后,完整的大圓盤的質量為
M0=πR2ρ
大圓盤的質心坐標為
x0=0y0=0
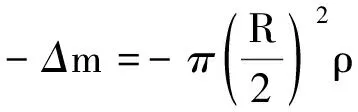
根據質心坐標系,便可得到被挖去圓孔的薄圓盤的質心坐標為
評注:由此可見,對于此類幾何均勻分布的有孔物體,巧用“補償法”進行恰當的分割填補,再進行計算,比較簡便.
2 在電磁場中的應用
2.1 用補償法解決電場中的問題
【例3】一個絕緣的剛性細圓環,半徑為R,質量為M,可以繞垂直于紙面的軸O自由旋轉,但不能平動.此環長度均勻帶電,電荷量為Q.在A點剪下一個小缺口,其空隙長度為l.開始時圓環靜止不動,接通一個勻強電場E,讓E既垂直于軸O,又垂直于半徑OA,如圖3所示,求圓環旋轉的最大角速度.
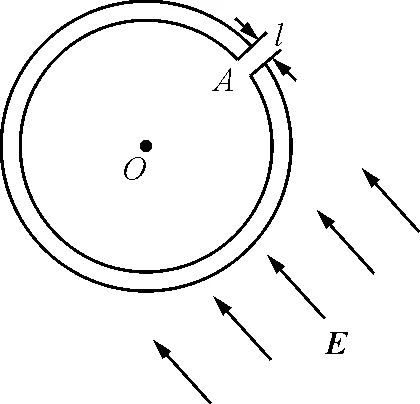
圖3
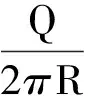
根據動能定理
解得
評注:通過恰當的分割填補,可以使原來不在公式適用范圍之內的問題變為可以直接應用公式解決的問題.
2.2 用補償法解決磁場中的問題
【例4】一無限長圓柱,偏軸平行地挖出一個圓柱空間,兩圓柱軸間距離OO′=d,圖4為垂直于軸的截面.設大圓柱間存在勻強磁場,磁感應強度隨時間t線性增大,即B=-kt.挖出的圓柱空間磁感應強度為零.現在空腔里放一長為L,與OO′在同一平面內且成60°角的金屬桿AO′C.求桿中的感生電動勢.
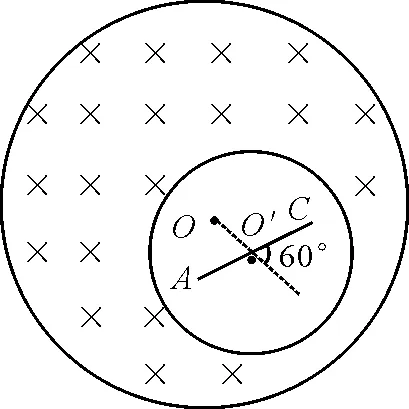
圖4

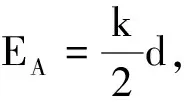
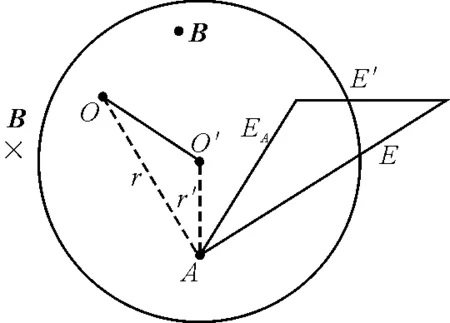
圖5
評注:應用補償法,在空腔內填補大小相同、變化率相同但方向相反的均勻磁場,使空腔內任意一點的感生電場可以看成是兩個無限長的圓柱體產生的電場的疊加,使問題由繁變簡,得到有效的解決.
2.3 用補償法解決復合場中的問題
【例5】如圖6(a)所示,A1和A2是兩塊面積很大、相互平行又相距較近的帶電金屬板,相距為d,
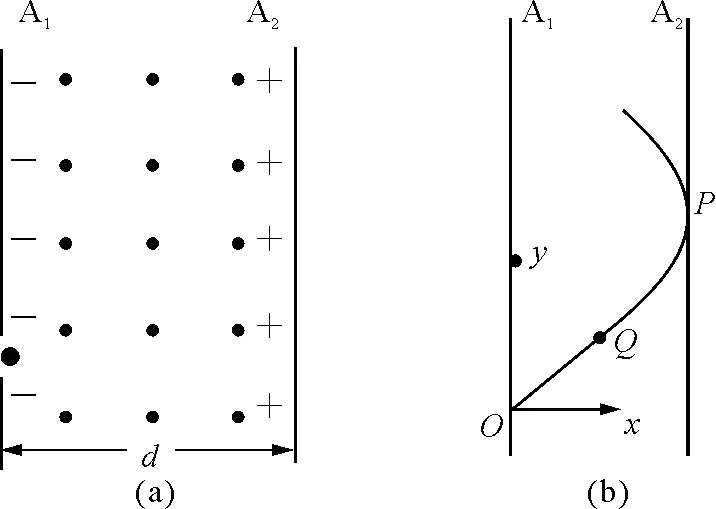
圖6
兩板間電勢差為U.同時在兩板間還有方向與均勻電場正交而垂直紙面向外的勻強磁場.一電子在左側帶負電的板A1上的小孔無初速釋放.為使該電子不碰到右側帶正電的板A2.問所加磁場的磁感應強度至少要多大?(設電子所受的重力不計)
解析:電子在電磁場的復合場中做復雜的曲線運動,可以用數理方法解決,相對較為繁瑣.可用補償法處理,把復雜運動巧妙分解.
根據題意,電子進入板間初速度為零,設想此時電子具有沿圖6(b)所示的y方向的速度+v和-v,使+v引起的磁場力恰好與電子在極板間受到的電場力相平衡,即v的大小滿足
即
由此可見,+v引起的磁場力和電場力平衡使電子沿y軸方向做勻速直線運動,-v引起的磁場力使電子以-v做勻速圓周運動,于是,電子的運動結合起來,可視為是一個速度為v的向上的勻速直線運動和速率為v的勻速圓周運動的合成.
對勻速圓周運動,有
而要求電子不碰到A2板,則必須有
由上可得
評注:運用補償法,引入大小相同方向相反的速度,將粒子的復雜運動分解成同一平面內的勻速圓周運動與勻速直線運動的合成,巧妙地運用了運動的合成和分解知識來處理復雜運動的過程,使問題簡化.

