定性分析法在含有數(shù)值判斷題分析中的作用
邱會(huì)明
(南京金陵中學(xué) 江蘇 南京 210005)
對(duì)含數(shù)值的判斷題,先根據(jù)物理規(guī)律列出方程,然后把具體數(shù)值代入方程,用計(jì)算的結(jié)果可以做出精確的判斷.一般情況下,對(duì)于含數(shù)值的判斷題用計(jì)算的方法是行之有效的.但在有的情況下,所給的數(shù)值之間具有倍數(shù)關(guān)系,是巧合,還是隱藏“天機(jī)”?筆者發(fā)現(xiàn),若能根據(jù)數(shù)值之間的倍數(shù)關(guān)系,采用定性分析的方法,不僅能使物理的圖景更清晰、內(nèi)涵更深刻,而且能把學(xué)生引入全新的思維意境,能培養(yǎng)學(xué)生良好的思維品質(zhì).下面通過一例來說明之.
1 例題和計(jì)算的方法
【例】以v0=24 m/s的初速度從地面豎直向上拋出一個(gè)物體,上升的最大高度H=24 m.設(shè)空氣阻力大小不變,則上升過程和下降過程中動(dòng)能和勢(shì)能相等的高度分別是(以地面為零勢(shì)能參考面,g=10 m/s2)
A.等于12 m,等于12 m
B.大于12 m,大于12 m
C.小于12 m,大于12 m
D.大于12 m,小于12 m
解:設(shè)空氣阻力為f,上升過程和下降過程中動(dòng)能和勢(shì)能相等的高度分別是h1、h2,從拋出點(diǎn)運(yùn)動(dòng)到最高點(diǎn)的過程中,由能量守恒定律得
(1)
從拋出點(diǎn)上升運(yùn)動(dòng)到高度h1的過程中,由能量守恒得
(2)
由題意得
mgh1=Ek1
(3)
由(1)、(2)、(3)式得
從最高點(diǎn)運(yùn)動(dòng)到高度h2的過程中,由能量守恒得
mgH=mgh2+f(H-h2)+Ek2
(4)
由題意得
mgh2=Ek2
(5)
由(1)、(4)、(5)式得
由h1、h2的具體數(shù)值可以得出正確答案為選項(xiàng)D.
點(diǎn)評(píng):上述解法中,通過過程分析列出了能量守恒定律的方程,計(jì)算后做出了準(zhǔn)確的判斷.從解題的過程來看,符合一般的思維方式.但問題在于,題中所給的12 m恰好是題設(shè)中物體上升最大高度的一半,能否抓住數(shù)值之間的倍數(shù)關(guān)系,用定性分析的方法來解決呢?我們知道,上述問題是一個(gè)典型的物理模型,存在著一定的規(guī)律性.這種規(guī)律性從不同的角度去分析和認(rèn)識(shí),從而會(huì)產(chǎn)生不同的思維方法,這種規(guī)律性附加了某種特定的條件后,就必定能做出一定范圍的判斷.由此可見,上述問題可以從多角度采用定性分析的方法去解決.
2 定性分析的方法
2.1 圖示法
如圖1所示,設(shè)矩形的“面積”表示能量的大小,用矩形的總面積表示物體拋出時(shí)的動(dòng)能,圖1(a)、(b)的總面積相等.用E1、E2分別表示物體從拋出點(diǎn)上升到最高點(diǎn)和中點(diǎn)時(shí)因阻力做功而損失的機(jī)械能,顯然,E1>E2.圖中陰影面積各占余下面積的一半,分別記為
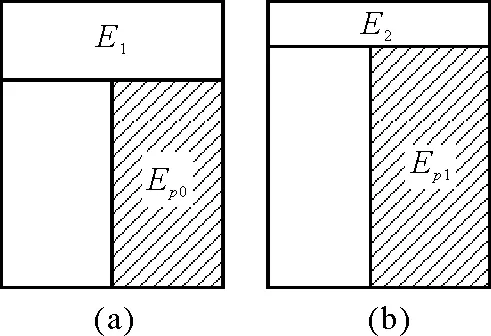
圖1
Ep1=mgh1
比較圖1(a)和(b)可得
用同樣的方法可以得出
由此可以得出,正確答案為選項(xiàng)D.
2.2 假設(shè)法
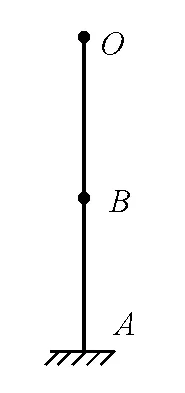
圖2
如圖2所示,B點(diǎn)為物體豎直方向運(yùn)動(dòng)過程的中點(diǎn).假設(shè)豎直上升過程中沒有阻力,則物體在B點(diǎn)的動(dòng)能與重力勢(shì)能相等.當(dāng)存在恒定阻力時(shí),要使物體能達(dá)到O點(diǎn),則要增大物體在B點(diǎn)的動(dòng)能.因而物體運(yùn)動(dòng)到B點(diǎn)時(shí),其動(dòng)能比重力勢(shì)能大,因此,上升過程中動(dòng)能和勢(shì)能相等的高度大于12 m.在下降過程中,按照同樣的分析方法可得出物體動(dòng)能和勢(shì)能相等的高度小于12 m.
2.3 等效法
物體在豎直上升的過程中,由于受到恒定阻力的作用,因而使得物體的加速度大于重力加速度,其等效“重力勢(shì)能”變大.物體運(yùn)動(dòng)到B點(diǎn)時(shí),物體的等效“重力勢(shì)能”等于動(dòng)能,其動(dòng)能比重力勢(shì)能大,因此,上升過程中動(dòng)能和重力勢(shì)能相等的高度大于12 m.在下降過程中,按照同樣的分析方法可得出物體動(dòng)能和勢(shì)能相等的高度小于12 m.
2.4 比例法
物體在豎直上升的過程中,由于動(dòng)能的減少量與克服阻力做功成正比,因此,B點(diǎn)的動(dòng)能為拋出點(diǎn)動(dòng)能的一半.而物體在B點(diǎn)的重力勢(shì)能是O點(diǎn)重力勢(shì)能的一半.顯然,物體的初動(dòng)能大于O點(diǎn)的重力勢(shì)能,故可得出物體在B點(diǎn)的動(dòng)能比其重力勢(shì)能大的結(jié)論.用同樣的方法可得出物體下降過程中物體在B點(diǎn)的動(dòng)能比其重力勢(shì)能小,由此可以得出前述的正確結(jié)論.
2.5 圖像法
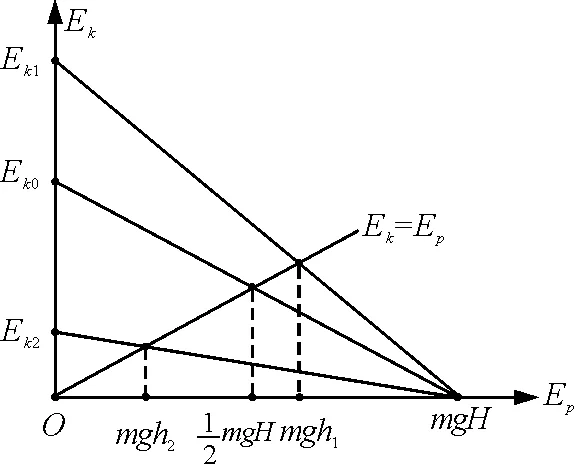
設(shè)物體的初動(dòng)能為Ek1,物體上升的最大高度為H,從拋出點(diǎn)上升高到某一高度h的過程中,由能量守恒定律可得物體在h處的動(dòng)能為
設(shè)物體從高度H下落,物體落地的動(dòng)能為Ek2(Ek2 設(shè)物體在豎直上拋的過程中不計(jì)阻力,物體的初動(dòng)能為Ek0,由能量守恒定律可得物體在h處的動(dòng)能為 Ek=Ek0-mgh=Ek0-Ep 上述動(dòng)能與勢(shì)能的關(guān)系可用圖3表示.從圖中可以看出,在物體上升的過程中,動(dòng)能和勢(shì)能相等的高度為 圖3 在物體下降的過程中,動(dòng)能和勢(shì)能相等的高度為 從此可見,用定性分析的方法解析問題,揭示了深刻的物理內(nèi)涵,其作用是不可忽視的,也是用計(jì)算的方法所不能替代的.在實(shí)施新課程的今天,教師應(yīng)把教學(xué)的重點(diǎn)放在學(xué)生思維能力的培養(yǎng)上,抓住契機(jī),引導(dǎo)學(xué)生去發(fā)現(xiàn)問題、思考問題,這樣才能把培養(yǎng)學(xué)生的能力落在實(shí)處.