彈簧類問題難點的探究與思考
郝玉玲
(錫林浩特市第四中學(xué) 內(nèi)蒙古 錫林浩特 026000)
在中學(xué)階段,涉及的彈簧都不考慮其質(zhì)量,稱之為“輕彈簧”.這是一種常見的理想化物理模型.彈簧類問題多為綜合性問題,涉及的知識面廣,是物理學(xué)習(xí)的難點之一.常見的彈簧問題有如下幾種.
1 彈力是由形變而決定大小和方向的力
當題目中出現(xiàn)彈簧時,要注意彈力的大小與方向時刻要與當時的形變相對應(yīng).在題目中一般應(yīng)從彈簧的形變分析入手,先確定彈簧原長位置,現(xiàn)長位置,找出形變量x與物體空間位置變化的幾何關(guān)系,分析形變所對應(yīng)的彈力大小、方向,以此來分析計算物體運動狀態(tài)的可能變化.
【例1】如圖1所示,四個完全相同的彈簧都處于水平位置,它們的右端受到大小皆為F的拉力作用,而左端的情況各不相同.
圖1(a)中彈簧的左端固定在墻上.
圖1(b)中彈簧的左端受大小也為F的拉力作用.
圖1(c)中彈簧的左端拴一小物塊,物塊在光滑的桌面上滑動.
圖1(d)中彈簧的左端拴一小物塊,物塊在有摩擦的桌面上滑動.
若認為彈簧的質(zhì)量都為零,以l1,l2,l3,l4依次表示四個彈簧的伸長量,則有

圖1
A.l1>l2B.l2>l3
C.l1>l4D.l2=l4
解析:當彈簧處于靜止(或勻速運動)時,彈簧兩端受力大小相等,產(chǎn)生的彈力也相等,用其中任意一端產(chǎn)生的彈力代入胡克定律即可求其形變.當彈簧處于加速運動狀態(tài)時,以彈簧為研究對象,由于其質(zhì)量為零,無論加速度a為多少,仍然可以得到彈簧兩端受力大小相等.由于彈簧彈力與施加在彈簧上的外力F是作用力與反作用力的關(guān)系,因此,彈簧的彈力也處處相等,與靜止情況沒有區(qū)別.在題目所述四種情況中,由于彈簧的右端受到大小皆為F的拉力作用,且彈簧質(zhì)量都為零,根據(jù)作用力與反作用力關(guān)系,彈簧產(chǎn)生的彈力大小皆為F;又由四個彈簧完全相同,根據(jù)胡克定律,它們的伸長量皆相等.所以正確選項為D.
2 彈簧的彈力不突變
因彈簧(尤其是軟質(zhì)彈簧)其形變發(fā)生改變過程需要一段時間,在瞬間內(nèi)形變量可以認為不變.因此,在分析瞬時變化時,可以認為彈力大小不變.
【例2】(2001年高考上海題)如圖2(a)所示,一質(zhì)量為m的物體系于長度分別為l1,l2的兩根細線上,l1的一端懸掛在天花板上,與豎直方向夾角為θ,l2水平拉直,物體處于平衡狀態(tài).現(xiàn)將l2線剪斷,求剪斷瞬時物體的加速度.
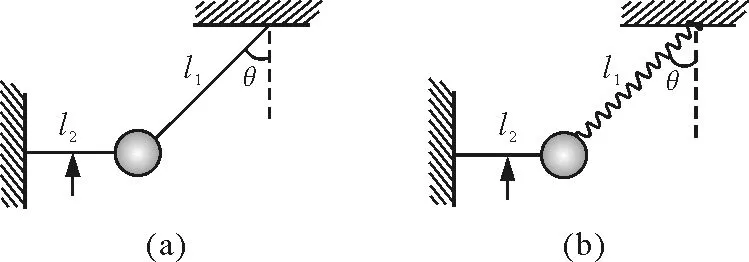
圖2
(1)某同學(xué)對該題解法:
設(shè)l1線上拉力為T1,l2線上拉力為T2,重力為mg,物體在三力作用下保持平衡,則
T1cosθ=mgT1sinθ=T2T2=mgtanθ
剪斷線的瞬間,T2突然消失,物體即在T2反方向獲得加速度.因為mgtanθ=ma,所以加速度a=gtanθ,方向在T2反方向.
你認為這個結(jié)果正確嗎?請對該解法作出評價并說明理由.
(2)若將圖2(a)中的細線l1改為長度相同、質(zhì)量不計的輕彈簧,如圖2(b)所示,其他條件不變,求解的步驟與(1)完全相同,即a=gtanθ.
你認為這個結(jié)果正確嗎?請說明理由.
分析:(1)結(jié)果不正確.因為l2被剪斷的瞬間,l1上張力的大小發(fā)生了突變,此瞬間
T1=mgcosθa=gsinθ
(2)結(jié)果正確,因為l2被剪斷的瞬間、彈簧l1的長度不能發(fā)生突變、T1的大小和方向都不變.
3 彈簧的彈力做功
在求彈簧的彈力做功時,因該變力為線性變化,可以先求平均力,再用功的定義進行計算,也可根據(jù)動能定理或能量守恒和轉(zhuǎn)化定律求解.同時要注意彈力做功的特點
彈力的功等于彈性勢能增量的負值.
彈性勢能的公式為
高考不作定量要求,可作定性討論.因此,在求彈力的功或彈性勢能的改變時,一般從能量守恒與轉(zhuǎn)化的角度來求解.

圖3
【例3】A,B兩木塊疊放在豎直輕彈簧上,如圖3所示.已知木塊A,B質(zhì)量分別為0.42 kg和0.40 kg,彈簧的勁度系數(shù)κ=100 N/m.若在木塊A上作用一個豎直向上的力F,使A由靜止開始以0.5 m/s2的加速度豎直向上做勻加速運動(g=10 m/s2).
(1)求使木塊A豎直做勻加速運動的過程中,力F的最大值;
(2)若木塊由靜止開始做勻加速運動,直到A,B分離的過程中,彈簧的彈性勢能減少了0.248 J,求這一過程F對木塊做的功.
分析:此題難點和失分點在于能否通過對此物理過程的分析后,確定兩物體分離的臨界點,即當彈簧作用下的兩物體加速度、速度相同且相互作用的彈力N=0時恰好分離.
解題方法與技巧:
當F=0(即不加豎直向上力F時),設(shè)A,B疊放在彈簧上處于平衡時彈簧的壓縮量為x,有
κx=(mA+mB)g
(1)
對A施加F力,分析A,B受力如圖4所示.
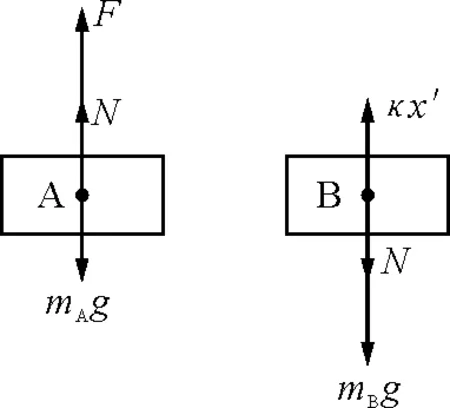
圖4
對AF+N-mAg=mAa
(2)
對Bκx′-N-mBg=mBa′
(3)
當N≠0時,A,B有共同加速度a=a′,由(2)式知,欲使A勻加速運動,隨N減小F增大.
當N=0時,F(xiàn)取得了最大值Fm, 即
Fm=mA(g+a)=4.41 N
又當N=0時,A,B開始分離,由(3)式知,此時,彈簧壓縮量
κx′=mB(a+g)
(4)
A,B共同速度
v2=2a(x-x′)
(5)
由題知,此過程彈性勢能減少了
Wp=Ep=0.248 J
設(shè)力F的功WF等于機械能的增量.
(6)
聯(lián)立(1)、(4)、(5)、(6)式,且注意到
Ep=0.248 J
可知
WF=9.64×10-2J
4 與物體平衡相關(guān)的彈簧問題
【例4】(1999年高考全國物理卷)如圖5所示,兩木塊的質(zhì)量分別為m1和m2,兩輕質(zhì)彈簧的勁度系數(shù)分別為κ1和κ2,上面木塊壓在上面的彈簧上(但不拴接),整個系統(tǒng)處于平衡狀態(tài).現(xiàn)緩慢向上提上面的木塊,直到它剛離開上面彈簧.在這過程中下面木塊移動的距離為
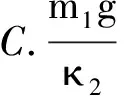
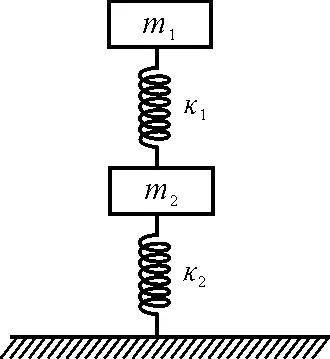
圖5
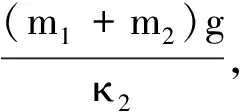
正確答案為選項C.

