多普勒效應的最簡規律

雷裕波

(昭平中學 廣西 賀州 546800)

當波源與觀測者之間存在相對運動時，觀測者觀測到的頻率與波源發射波的頻率不同，這種現象就是多普勒效應．引起多普勒效應的根本原因在于波源與觀測者之間存在相對運動．在低速傳播的機械波里所產生的多普勒效應比較容易掌握.然而當波源或觀測者的運動速度較高時，必須要考慮時空變換的相對效應，此時的多普勒效應會遵循怎樣的規律呢？本文就從洛倫茲時空變換的角度，闡述各種情形下的多普勒效應，并從中總結出多普勒效應所遵循的最簡規律 ．

1 縱向多普勒效應

設有三個慣性參照系，如圖1所示．

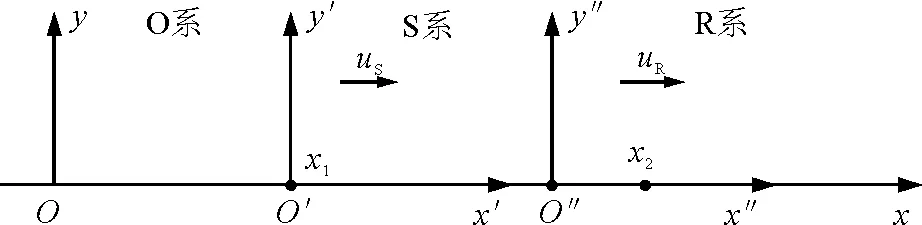
圖1

媒質(場)參照系，即靜系，簡稱O系，相應的坐標系為xOy．

波源參照系，即動系，簡稱S系，以波源S所在處為坐標原點，建立坐標系x′O′y′．

觀測者參照系，即動系，簡稱R系，以觀測者R處為坐標原點，建立坐標系x″O″y″．

由圖1可看出,O、S、R系的x軸重合,令t=0時刻，O、O′、O″三原點重合，S系以速度uS、R系以速度uR同時沿O系的x軸正方向運動，此時波源S在O處發射第1個波峰，至t時刻，S系運動到O系的x1處，波源恰好發射第2個波峰，且第1波峰以速度vφ(相對O系)運動到O系的x2處，在S系及R系上表示t時刻的這兩個相鄰波峰的相應坐標分別如下：

O系：(0，0) (x1，t) (x2，t)

S系：(0，0) (x1′，t1′) (x2′，t2′)

R系：(0，0) (x1″，t1″) (x2″，t2″)

由洛倫茲的時空變換得

對S系：

(2)

(4)

對于R系，有完全相似的關系式.

由(1)、(2)式得

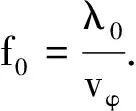
由(3)、(4)兩式得

由此可見，t2′與t1′在S系上看來并非同一時刻，即x2′-x1′不是在S系觀測到的波長.由于t2′比t1′早|Δt′|時間,所以在S系觀測到的波長應為

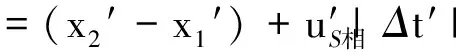
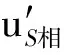
聯立前面有關各式，解得

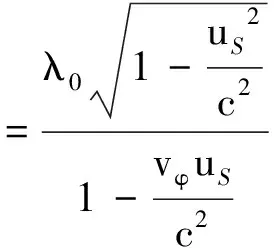
設TS為波源發射波的周期，則

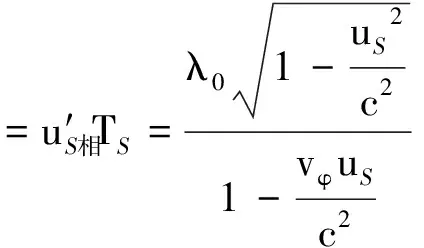
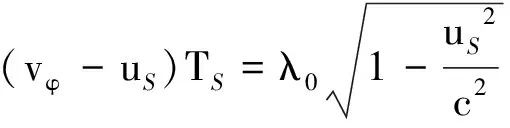
(5)

同理，在R系中不難得到

(6)

(6)式中，TR為在R系上的觀測者所觀測到的周期．

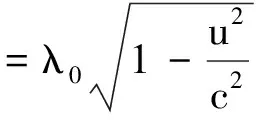
若不考慮動系相對靜系的時空收縮效應,則λ洛=λ0；此時多普勒效應屬于伽利略變換下的效應.若設T0為波在靜系里沿u方向傳播的周期，則λ0=vφT0.據洛倫茲變換知，當靜系里的時間間隔為T0時，在動系里測得的時間間隔便為

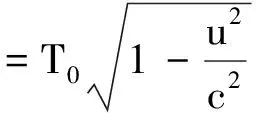
于是λ洛=vφT洛，顯然在r0方向上亦有

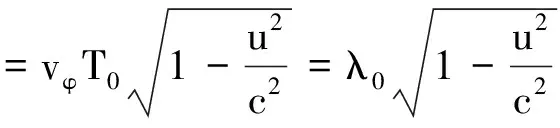
此時T0、λ0則分別表示波在靜系里沿r0方向上傳播的周期和波長，且有可能發生變化.例如當波源運動時，沿u方向傳播的波波長λ0最小,而沿與u相反方向傳播的波波長λ0最大，在垂直于u方向上傳播的波λ0取值在此兩者之間，但通常情況下λ0不必求出．于是(5)、(6)式可寫成統一式

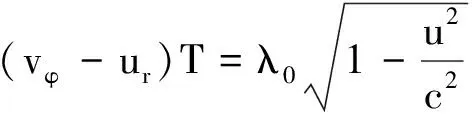
(7)

由此可見上述(5)、(6)兩式應視作(7)式的特殊情形；然而(7)式的正確性及普遍性還有待于后面進一步的論證．

設

由(5)、(6)式得

(8)

(8)式為縱向多普勒效應的頻率公式.顯然對于機械波，由于波速vφ及波源或觀測者的運動速度都遠小于光速，相對效應很不明顯，所以有

(9)

(9)式就是機械波的縱向多普勒效應的頻率關系式，據此式可知，當觀察者運動的方向與傳向觀測者的波的傳播方向相同時，uR>0，使觀測到的頻率fR降低，反之升高.當波源的運動方向與傳向觀測者的波的傳播方向相同時，uS>0，使觀測到的頻率升高，反之降低．

對于光波而言，vφ=c，當uR或uS比較大時，相對效應較明顯，此時由(8)式得

設u為觀測者相對波源的相對運動速度，據洛倫茲速度變換關系有

于是上式變為

(10)

由(10)式知，當觀測者遠離波源運動時，u取正，使觀測到的頻率降低；當觀測者靠近波源運動時，u取負，使觀測到的頻率升高．當u?c時，即觀測者相對波源做低速運動時，(10)式可化為

即

Δf為由多普勒效應所引起的頻移量．

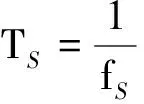
與前面的(7)式對比，此式應有類似的物理意義．

以上推導得出的(8)、(9)、(10)式，其正確性可從另外的角度加以證明(略)，從而知(7)式適用于縱向多普勒效應．

2 橫向多普勒效應

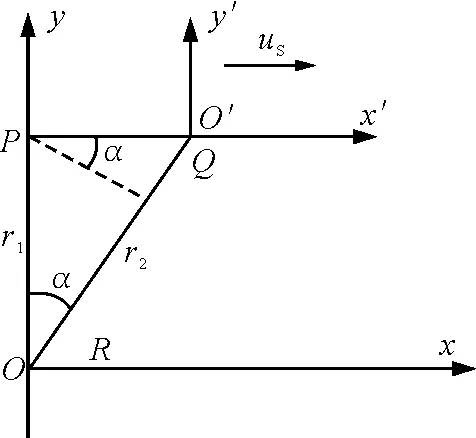
圖2

如圖2所示，觀測者相對媒質靜止，以觀測者R處為原點O，建立靜止的參照系R，以波源S處為原點O′，建立運動的參照系S，兩系的x軸相互平行.在R系看來，t=0時刻，波源S位于R系的y=r1的P處，并以速度uS沿x軸正方向勻速運動，同時波源發射的波沿y軸負方向傳向觀測者R處．設波源的周期為TS，頻率為fS，觀測者觀測到的周期為TR，頻率為fR，如果前述(7)式依然適用，則對觀測者即R系而言，因為uR= 0，所以

而

由λR伽=λR洛得

fR=f0

(11)

對波源即S系而言，因波沿y軸負方向傳向觀測者，故伽利略相對速度為vφ,所以有

由λS伽=λS洛得

(12)

由(11)、(12)兩式得

(13)

(13)式為橫向多普勒效應的頻率關系式,其正確性可作如下證明：如圖2所示，設相對R系波的圓頻率為ωR,相對S系波的圓頻率為ωS.在R系上看，經一微小時間Δt，波源沿x軸正方向由P處運動到Q處，在S系上看相應的時間為Δt′，波振動的位相差為Δφ′=ωSΔt′；而在R系上看，觀測者接收到分別由P、Q兩處傳來的兩次波振動,其位相差應為

式中r2為Q,O間的距離．當Δt很小時，α很小，則此式中

故

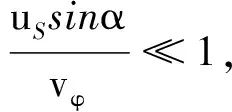
再利用ωS=2πfS及ωR=2πfR，便得

此式與(13)式相同，表明：

(1)上面的(7)式適用于橫向多普勒效應；

(2)橫向多普勒效應不如縱向多普勒效應明顯, 因為當uR=0時,有

對機械波而言，uS?c，故fR橫≈fS，即橫向多普勒效應很不明顯，難于觀測到．

3 斜向多普勒效應

下面討論更為一般的多普勒效應——斜向多普勒效應．如圖3所示，觀測者R靜止，以R處為原點O，建立坐標系xOy，簡稱R系.

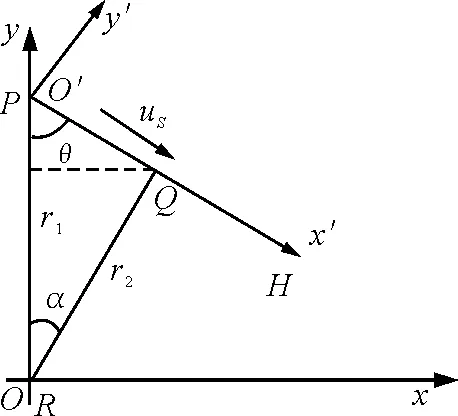
圖3

在y=r1的P處，有一以速度uS沿PH方向運動的波源S，PH與PR成θ角．以波源S處為原點O′，建立坐標系x′O′y′,簡稱S系，x′軸與PH重合，t=0時刻波源剛好在P處，假設(7)式仍然成立，但此時沿y軸負方向傳給觀測者的波在S系上的伽利略相對波速為(vφ-uScosθ)，于是得

及

vφTR=λ0

由此得

(14)

(14)式的正確性，亦可仿照前述的方法加以驗證．設在R系上，觀測者觀測到的圓頻率為ωR；在S系上，波源發射波的圓頻率為ωS，自t=0時刻開始，波源由R系的P處沿PH方向(即S系的x′軸正方向)以速度uS運動，經一微小時間Δt運動到Q處，則觀測者接收到來自P、Q兩處的波振動，其位相差為

因Δt很小，α角很小，所以有

故

而在S系上看，波源在P、Q兩處發射的波振動位相差為Δφ′=ωSΔt′(Δt′為在S系上觀測的時間)，根據位相不變原理得Δφ=Δφ′，即

根據洛倫茲變換，有

并代入上式得

令ωR=2πfR，ωS=2πfS，于是得

此式與(14)式一致.

綜上所述，知(7)式既適用于縱向也適用于橫向多普勒效應.多普勒效應的這一最簡規律可表述為：在任一慣性系里，伽利略變換下的相對波長等于洛倫茲變換下的收縮波長．