基于PSO-RBF神經網絡的模擬電路故障診斷研究
郭 珂, 傘 冶, 朱 亦
(哈爾濱工業大學 黑龍江 哈爾濱 150001)
當今社會,電子設備廣泛應用于人們科研、生產、生活的各個領域。電子設備中的電路系統分為模擬電路和數字電路兩個部分,數字電路由于輸入輸出信號比較規范,電路集成度高等自身特點決定了其出現故障的可能性較小,而且即使出了故障也比較容易診斷。理論分析和長期的實際使用經驗均表明,雖然電子設備中數字電路部分超過80%,但80%以上的故障均來自模擬電路[1],因此模擬電路故障診斷的研究具有重要意義。
筆者首先利用主成分分析方法對故障信息作特征提取,然后采用PSO算法優化RBF網絡,最后將訓練好的RBF網絡模型用于模擬電路的故障。
1 基于主成分分析的模擬電路故障特征提取
主成分分析(Principal Component Analysis, PCA)實質是上把高維數據信息線性投影到低維子空間中,用維數較少且相互獨立的新變量來表征原變量所提供的絕大部分信息,從而簡化問題處理的難度并提高信噪比。采用主成分分析方法對原始故障數據集進行預處理,可以在不損失有用信息的情況下提取出故障本質特征向量。將提取出的特征向量送入RBF網絡進行處理,由于訓練數據的規模得到約簡,因而可以簡化神經網絡的結構,提高網絡訓練速度進而達到提高診斷效率的目的。
假定模擬電路的每一故障模式對應有c個特征參數,每種故障模式有l個樣本數目,構成一個l×c原始故障樣本矩陣X。
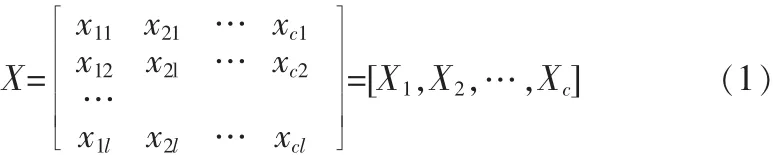
其中:Xi=[xi1,xi2,…,xil]T,i=1,2,…,c。
根據PCA方法的基本原理,給出基于PCA的故障數據壓縮及特征提取算法步驟如下:
step 1:標準化
1)計算原始數據矩陣X矩陣的均值向量xˉ;

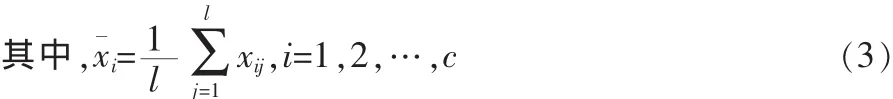
2)計算中心平移矩陣X^,即把每維數據減去相應的均值;

step 2:計算數據的協方差矩陣∑c×c
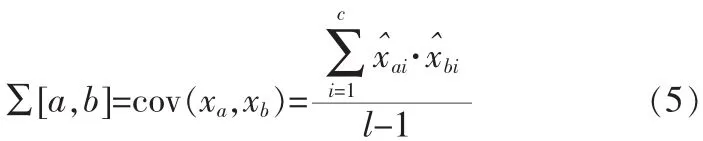
其中,a=1,2,…c;b=1,2,…,c。
step 3:對協方差矩陣∑進行特征分析,使∑P=PΛ
其中,Λ=diag[λ1,λ2,…,λc],P=[p1,p2,…,pc],它們分別是協方差矩陣的特征值和對應的特征向量。將特征值按照由大到小的順序排列,對應的特征向量也作相應排列。
step 4:主成分個數的選取
確定主成分個數的方法有Akaike信息準則法、平均特征值法和累計方差貢獻率法等,文中采用累計方差貢獻率法。
1)取前 d 個 特 征 值 Λd=diag[λ1,λ2,… ,λd]和 特 征 向 量Pd=[p1,p2,…pd]作為子空間的基底,由[p1,p2,…pd]構成主元空間,由[Pd+1,Pd+2,…,Pn]構成殘差空間;
2)具體如何確定d需要引入方差貢獻率的定義:

ηi稱為第i個主成分pi的方差貢獻率。如果只取前d(d step 5:求取故障特向量 第 i個故障特征向量為 ti=Xpi,其中,i=1,2,…,d。 徑向基函數神經網絡 (Radial Basis Function Neural Networks,RBF網絡)是一種3層前饋網絡,以函數逼近論為理論基礎,模擬了人腦中局部調整、相互覆蓋接收域的神經網絡結構。RBF網絡是一種局部逼近網絡,具有結構簡單、學習收斂速度快且對于非線性連續函數具有一致逼近性等優良特性,因而在函數逼近和模式分類領域中顯現出比BP網絡更強的發展潛力。目前,RBF網絡已經廣泛應用于故障診斷[2-3]、非線性函數逼近、模式識別和圖像處理等領域。 圖1給出了拓撲結構為n-h-m的RBF網絡模型,它是一個以徑向基函數φ(·)為隱層單元的三層前向網絡:第一層是輸入層,由信號源節點組成,僅起到傳輸信號的作用,其中X=[x1,x1,…,xn]∈Rn為網絡輸入向量;第二層是隱層,隱單元的個數由所描述的問題而定,其中W∈Rh×m為輸出權矩陣;第三層是輸出層,對輸入模式做出響應,通常是簡單的線性函數,其中 y=[y1,y1,…,yn]∈Rm為網絡輸出,第 k 個輸出可以表 圖1 RBF神經網絡結構圖Fig.1 Structure of RBF neural networks 常用的徑向基函數有Gaussian函數、多二次函數、逆多二次函數和反射Sigmoid函數等,文中采用廣泛使用的Gaussian函數作為隱層單元的基函數。RBF網絡的學習過程通常可以分為兩步:第一步確定隱層節點的選取,包括節點個數h、中心位置ci和寬度σi;第二步確定隱層與輸出層之間的連接權矩陣W。通常情況下,當隱層節點個數以及中心位置、寬度確定后,隱層與輸出層之間權矩陣W的求取就可以采用線性優化策略,因而隱層節點數量和中心的確定是RBF網絡設計的核心問題。常用的學習算法有進化優選法、Kohonen中心選擇法、k-means聚類方法、梯度訓練方法以及正交最小二乘法等。盡管Chen等聲稱正交最小二乘算法能設計出最小結構的RBF網絡[4],但Sherstinsky和 Picard給出了反例[5],因而目前為止還沒有某種方法能夠在理論上求得上述參數的最優值,只能通過大量的實驗進行試湊。基于此,采用粒子群優化算法來訓練RBF網絡。 粒子群優化算法(Particle Swarm Optimization,PSO)是一種全局優化進化算法,它結構簡單易于實現、需要調整的參數較少,具有較強的全局收斂能力和魯棒性,能夠有效解決較為復雜的優化問題。在粒子群算法中,優化問題的每個可行解都看作搜索空間中的一個點(稱之為粒子),通過適應度函數值來評價每個粒子對應可行解的優劣。粒子具有位置和速度兩個屬性,它根據自身和同伴的飛行經驗來優化調整自己的位置和速度,迭代一定次數之后就會得到搜索空間中的全局最優解。粒子群算法的數學描述如下[6]: 假定一個由M個粒子組成的群體在D維搜索空間中以一定速度飛行,其中第i個粒子的位置和速度分別表示為Xi=(xi1,xi2,…,xid)和 Vi=(vi1,vi2,…,vid)。 用 pi=(pi1,pi2,…,pn)表示粒子自身迄今為止找到的最優解,pg=(pg1,pg2, …,pgn)表示整個種群迄今為止找到的最優解。粒子在找到pi和pg之后通過如下規則來更新自己的狀態: 式中,c1和c2為加速常數,它們表示粒子受社會知識和個體認知的影響程度,通常設為相同值,Clerc推導出,c1=c2=2.05,r1和 r2為介于(0,1)之間的隨機數;w為慣性權重因子,用于均衡粒子的全局探索能力和局部開發能力;vtid和xtid分別為粒子i在第t次迭代中第d維的速度和位置;ptid為粒子i在第d維的個體極值位置,ptgd為群體在第d維的全局極值位置。 實現PSO算法優化RBF網絡時需要解決如下3個問題: 1)參數編碼策略的選取 編碼方式通常分為向量編碼和矩陣編碼,文中采用向量編碼策略。在向量編碼策略中,每個粒子被編碼為一個向量,圖1所示的RBF網絡編碼后粒子位置和速度的維數為h×(n+1),RBF神經網絡隱層編碼策略如圖2所示。 圖2 RBF神經網絡隱層編碼策略Fig.2 Coding strategy for hidden layer of RBFNN 2)適應度函數的選取 網絡優化的最終目的是找到一組最優參數使得訓練樣本的均方誤差和最小,因此適應度函數可以選為: 3)算法終止條件的選取 算法終止條件的選取必須同時兼顧算法的學習精度和速度,通常為達到所要求的適應度閾值或者達到預先設定的最大迭代次數。PSO-RBF算法流程圖如圖3所示。 圖3 PSO-RBF算法流程圖Fig.3 Flow chart of PSO-RBF algorithm 為驗證文中所提方法的有效性,采用如下兩級三極管放大 圖4 兩級放大電路Fig.4 Two-level amplifying circuit 令C代表三極管集電極,E代表三極管發射極,令B代表三極管基極,OC代表開路故障,SC代表短路故障,建立表1所示的故障模式表。電路作為待診斷電路,電路中各元件參數值已在圖4中標出。 表1 故障模式表Tab.1 Table of fault mode 通過Cadence/OrCAD/PSpice電路仿真軟件對電路各種故障狀態進行仿真,開路故障模型用100 MΩ電阻和開路元件串聯,短路故障模型用1Ω電阻和短路元件并聯。圖5是電阻R1短路故障時的仿真電路圖,其他故障情況類似,因而不再一一給出。 圖5 電阻R1短路故障仿真電路圖Fig.5 Simulation circuit of resistance R1 short circuit fault 在圖4電路中共選取8個電壓測試節點:V1,V2,…,V6。為了便于進行下一步的故障特征提取,將測得數據進行歸一化處理,表2給出了用于訓練的一組歸一化處理后的數據。 為了減少RBF網絡的輸入向量維數,提高其訓練速度,對表2中的數據進行主成分分析,主成分分析后的數據如表3所示。圖6是前4個主成分的累積方差貢獻率圖,從圖6中可以看出,前4個主成分的貢獻率分別為45.98%,30.48%,13.60%和8.51%,前3個主成分的累積方差貢獻率為91%,前4個主成分的貢獻率已經達到了98.6%,文中選取前4個主成分作為RBF網絡的輸入。在網絡訓練過程中,隱層節點數選為6個,初始粒子數目經過多次試驗后確定為20個,網絡訓練誤差曲線如圖7所示。 表2 電壓測試數據Tab.2 Table of voltage measurement data 圖6 累積方差貢獻率圖Fig.6 Cumulative variances contribution rate 對各種故障情況下的放大電路進行300次Monte-Carlo實驗,將所得數據作為測試數據輸入訓練好的網絡用于故障診斷,經過300次的測試統計,所得故障診斷正確率如表4所示。可看出,文中所提方法的診斷效果較為理想,所有故障狀態的診斷正確率都能達到80%以上,其中一半以上的故障診斷正確率超過了95%,從而驗證了該方法的有效性。 模擬電路廣泛應用于生產、生活的各個領域,因而對其進行故障診斷研究具有重要現實意義。本文針對模擬電路傳統診斷方法的不足之處,提出采用基于粒子群優化的RBF網絡進行故障診斷,將主成分分析方法用于模擬電路的故障特征提取,從而約簡了網絡結構,提高了網絡訓練速度。在兩級放大電路的故障診斷實例中,高達80%以上的故障診斷正確率驗證了該方法的有效性和實用性。 表3 主成分分析后的測試數據Tab.3 Table of measurement data processed by PCA 圖7 網絡訓練誤差曲線Fig.7 Curve of training error for neural networks 表4 故障診斷正確率列表Tab.4 Table of diagnostic accuracy [1]Li F,Woo P Y.Fault detection for linear analog ic-the method of short-circuit admittance parameters[J].IEEE Transactions on Circuits and SystemsⅠ:Fundame, 2002, 49(1):105-108. [2]代睿.一種基于RBF神經網絡的智能故障診斷方法[J].北京聯合大學學報:自然科學版,2009,23(2):30-33.DAI Rui.Intelligent fault diagnosis based on RBF neural network[J].Journal of Beijing Union University:Natural Sciences,2009,23(2):30-33. [3]秦慶強,張曉安,李艾華,等.基于RBF網絡的模擬電路故障診斷算法[J].計算機仿真,2010,27(5):331-335.QIN Qing-qiang,ZHANG Xiao-an,LI Ai-hua,et al.Algorithm based on RBF artificial network for analog circuit faultdiagnosis[J].Computer Simulation,2010,27(5):331-335. [4]Chen S,Cowan N C,Grant P M.Orthogonal least squares learning algorithm for radial basis function networks[J].IEEE Transactions on Neural Networks, 1991, 2(2):302-309. [5]Sherstinsky A,Picard R W.On the efficiency of the orthogonal least squares training method for radial basis function networks[J].IEEE Transactions on Neural Networks,1996,7(1):195-200. [6]Shi Y,Eberhart R C.A modified particle swarm optimizer[C]//Proceedings of the IEEE conference on Evolutionary,1998:69-73.2 基于PSO優化的RBF神經網絡
2.1 RBF神經網絡
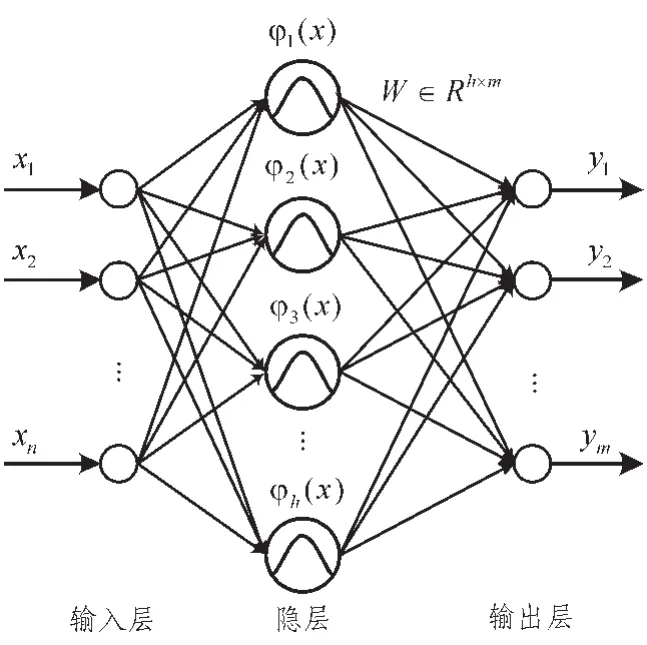
2.2 粒子群優化算法
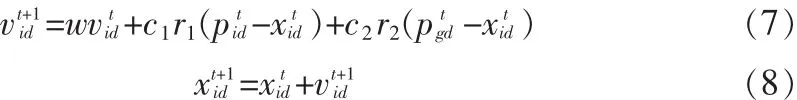
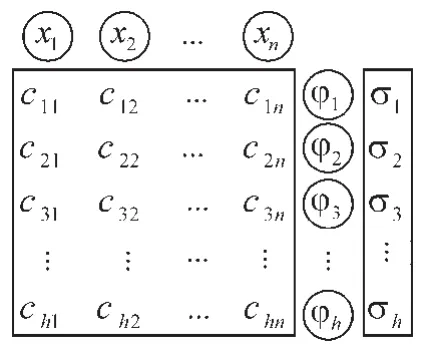
2.3 PSO-RBF算法實現


3 診斷實例
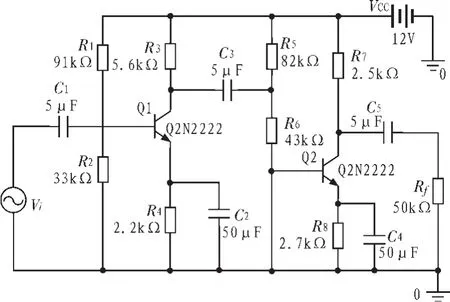

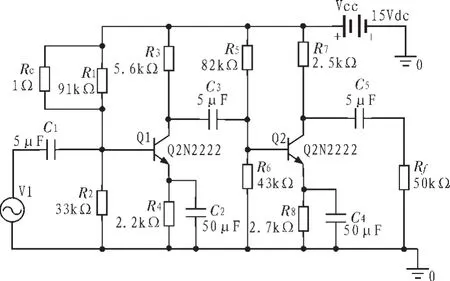
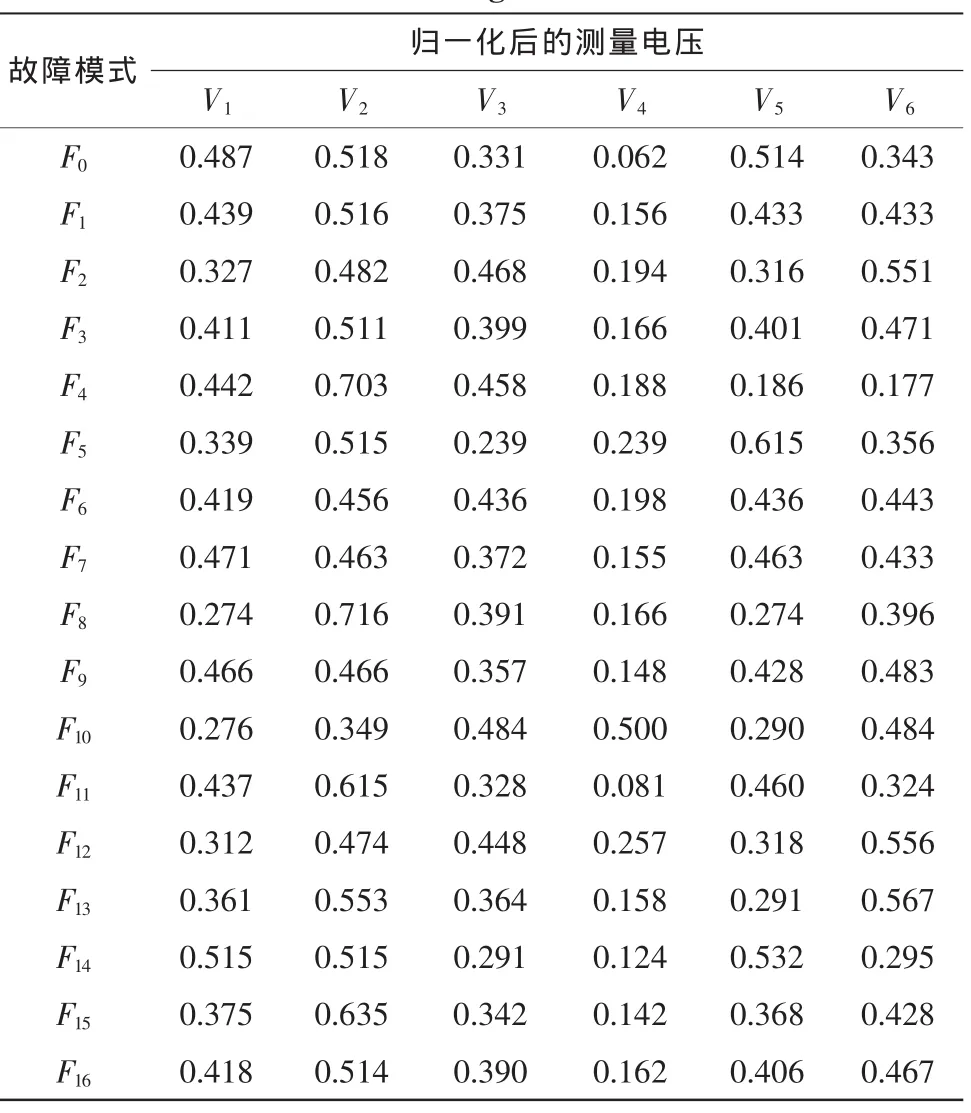
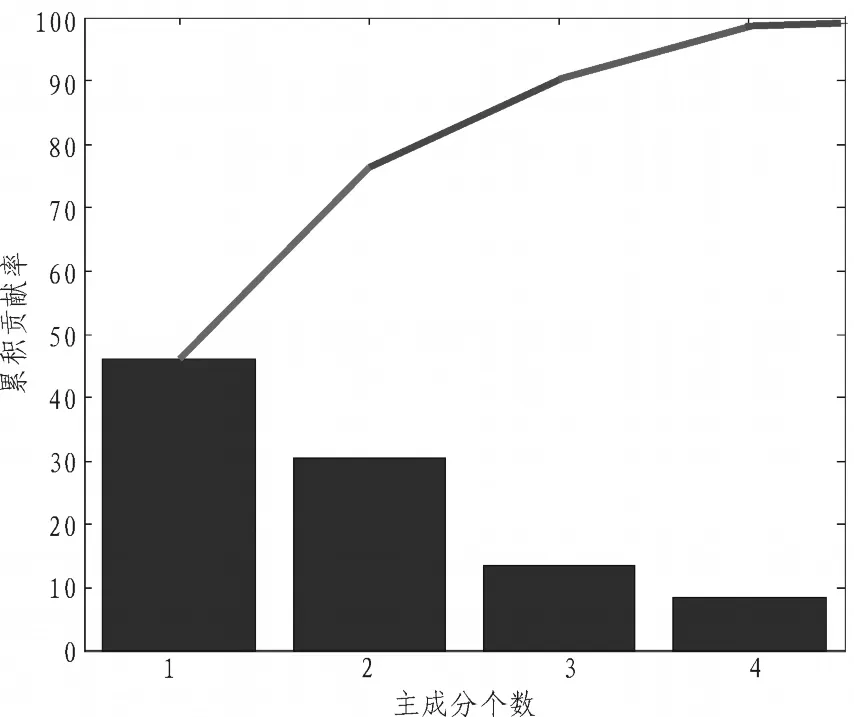
4 結 論