不變本征算符法計算各向異性Heisenberg反鐵磁系統的自旋波能量

成泰民， 葛崇員， 李青云， 孫樹生

(沈陽化工大學數理系，遼寧沈陽110142)

范洪義的論文［1-2］較詳細地介紹了不變本征算符法應用.因為體系的任意幺正變換聯系著同一個量子體系的不同表象之間的變換，所以，蘊含著該量子體系的嚴格一致的物理內容，這些幺正變換對該量子體系的描述是完全等價的.因此，在磁性物理及量子力學中普遍采用不同的幺正變換處理系統哈密頓量的對角化，求出元激發能量及基態能量.但是這一方法的關鍵是做出適合體系對角化的不同的幺正變換，利用幺正變換處理體系哈密頓量的過程也比較繁瑣［3-4］.封閉鏈的格林函數的運動方程法［5］(切斷近似法)也能夠處理體系元激發能量，利用此方法處理體系哈密頓量的過程中，關鍵是算符與哈密頓量之間的對易律，在此可以少考慮文獻［3-4］中的部分幺正變換(如Bogoliubov變換［3-4］等(注:文獻［3］與［4］的Bogoliubov變換表示形式不同，但都是幺正變換.只是文獻［3］中的Bogoliubov變換表示更凸顯其幺正性.)).本文用不變本征算符法處理線性近似下的Hamiltonian量體系的元激發能量，比上述兩種方法簡捷.

1 不變本征算符法［1-2］

或者

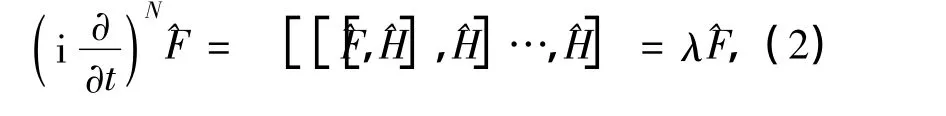
假設{|ψa〉，|ψb〉，…}是系統哈密頓量 ^H的本征態集合，構成希爾伯特空間的完備態矢量集，且對應的本征值為{Ea，Eb，…}.由(1)式、(2)式可得:

根據(3)式、(4)式可得:

從而可知，利用IEO方法無須涉及系統的具體量子態及波函數，可以直接對算符進行操作得出系統的能譜.IEO方法的關鍵是做出所研究系統的不變本征算符，這一方法極大地簡化了系統能譜的求解過程.但是IEO方法所計算的λ對應的不是系統的能級，而是能級差.

2 各向異性Heisenberg反鐵磁系統

設單位體積內總格點數為2N，可分為A、B兩個子晶格.X-Y-Z模型各向異性Heisenberg反鐵磁系統的Hamiltonian量表示為:

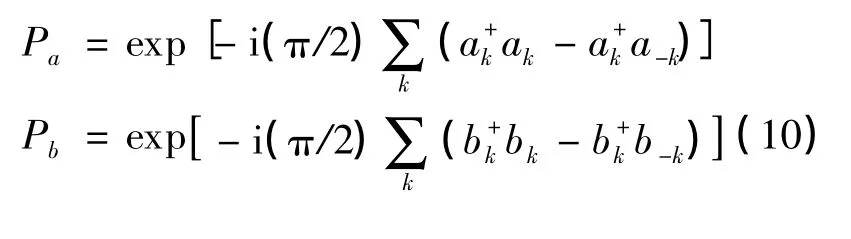
把(8)式、(9)式代入到(7)式，只保留到算符的二次項就可得線性近似下的哈密頓量，再進行(10)式的宇稱變換，并考慮哈密頓量的厄米性可得:

根據(13)～(15)式，可得:

從而得:

由(17)式得到非平庸解的條件為系數行列式等于零.從而可得:

在(18)式中，舍負取正并把(12)式中的系數代入到(18)式，可得X-Y-Z模型各向異性Heisenberg反鐵磁系統的自旋波能量:

(19)式與文獻［4］的結果一致(注:因在本文中令單位體積內總格點數為2N，所以，與文獻［4］系數上相差2倍.這是因為在文獻［4］中令單位體積內總格點數為 N之故).(19)式中“+”對應光學支自旋波能量，“-”對應聲學支自旋波能量.這與不同的幺正變換方法［3］所得到的結果完全一致.單從二粒子耦合體系［3］的元激發能量而言，這一結果與封閉鏈的格林函數運動方程法［5］計算的結果也一致，并且處理方法較相似，但是IEO方法更簡捷.

3 討論

(1)由(19)式，當X1=X2=X，X3=1時，可得X-Y-Z模型Heisenberg反鐵磁系統的自旋波能量如下:

由(20)式，當 X=1時，可得各向同性Heisenberg反鐵磁系統的自旋波能量=2JZS與文獻［6-7］一致.由此可知對稱性越高(有序度降低)，系統越易出現簡并現象［8］.這也與可觀測程度相關，系統具有某種對稱性，意味著存在某一物理量是不可觀測量.如果這種對稱性破缺了，那么這一物理量就成為可觀測量.在此對稱性破缺與X1≠X2相關，當X1=X2時，由(20)式可知，Heisenberg反鐵磁系統的自旋波能量出現簡并現象.

(2)利用IEO方法計算磁有序系統的自旋波能量非常方便，但是IEO方法不易給出磁有序系統的基態能量，并且利用IEO方法幾乎無法處理含有算符的三次項或者更高次項的Hamiltonian量體系(如電子-聲子耦合體系，磁振子-聲子耦合體系，聲子-聲子耦合體系，磁振子-磁振子耦合體系等)，在這一點IEO方法不如格林函數理論及量子場論的費曼圖技術.這是因為IEO方法計算的結果是能級差，對應的是磁有序系統的元激發能量;而且處理含有算符的三次項或者更高次項的Hamiltonian量體系時，涉及到算符與Hamiltonian量對易關系變得越來越復雜，并存在算符的冪次增大趨勢，對應Hamiltonian量的IEO又不易做出.因為線性近似下的Hamiltonian量只包含算符的二次項，所以，利用IEO方法及算符的對易關系，能夠簡捷地計算出線性近似下的Hamiltonian量體系的元激發能量.

［1］ Fan HongYi，Li Chao.Invariant‘Eigen-operator’of the Square of Schr?dinger Operator for Deriving Energy-level Gap［J］.Phys.Lett.A，2004，321:75-78.

［2］ Fan HongYi，Wu Hao.Deriving Vibrating Modes of Some Multiatom Molecules by Virtue of the Invariant Eigenoperator Method［J］.Modern Physics Letters B，2005，19(26):1361-1366.

［3］ 柳盛典，逯懷新，鄧汝剛.幺正變換與二粒子耦合體系哈密頓量的對角化技術［J］.大學物理，1993，12(5):25-26.

［4］ 何兵，應和平，季達人.X-Y-Z非各向同性反鐵磁Heisenberg系統的自旋波解［J］.物理學報，1996，45(3):522-527.

［5］ 蔡建華，龔昌德，姚希賢，等.量子統計的格林函數理論［M］.北京:科學出版社，1982:195-227.

［6］ 戴道生，錢昆明.鐵磁學(上冊)［M］.北京:科學出版社，1987:270-276，283，288.

［7］ 李正中.固體理論［M］.北京:高等教育出版社，2002:68-70，80，84.

［8］ 于祿，郝柏林，陳曉東.邊緣奇跡:相變和臨界現象［M］.北京:科學出版社，2005:36-47，87-92.