干摩擦下含間隙碰撞振動系統的動力學行為分析

王樹國，陳 英，劉大亮，楊 昊，翟海峰

（1.蘭州交通大學數理與軟件工程學院，甘肅蘭州，730070；2.蘭州交通大學博文學院土木工程系，甘肅蘭州，730070；3.蘭州交通大學機電工程學院，甘肅蘭州，730070）

機械系統中廣泛存在干摩擦結構，摩擦帶來磨損，使機械零件或部件之間出現間隙，產生運動副的分離與碰撞以及嚴重的系統振動與噪聲，從而降低機械系統的精度和運轉效率，甚至會導致整臺機器的破壞。因此，干摩擦下碰撞振動系統的動力學行為分析引起了眾多學者的關注。Shaw［1］研究了一單自由度簡諧激勵分段線性系統周期運動的穩定性，并分析了干摩擦系統的動力學響應以及由于摩擦導致的分岔行為（岔式分岔、Hopf分岔）。Cone等［2］采用數值方法分析了干摩擦單自由度雙面沖擊振子，結果表明系統存在周期倍化系列和黏滑碰撞運動。本文給出干摩擦下含間隙的雙自由度碰撞振動系統的滑動、黏滑和碰撞運動方程以及銜接條件，應用數值方法，結合理論分析，對該系統在帶速變化條件下的分岔現象進行研究，并討論激勵振幅和干摩擦對該系統黏滑及擦切運動的影響。

1 干摩擦碰撞振動系統模型

圖1所示為干摩擦下雙自由度碰撞振動系統的動力學模型。質量為M1的振子M1由剛度為K1的彈簧和阻尼系數為C1的黏性阻尼器相連接，振子M1與皮帶之間存在干摩擦力F1，作用在振子M1上的簡諧激勵為P1sin（ΩT＋τ）；質量為M2的振子M2由剛度為K2的彈簧和阻尼系數為C2的黏性阻尼器相連接，振子M2與皮帶之間存在干摩擦力F2，作用在振子M2上的簡諧激勵為當M1與M2的位移差絕對二者發生碰撞。皮帶的速度為V。

圖1 雙自由度摩擦碰撞振動系統模型Fig.1 Double－degree－of－freedom friction collision vibration system model

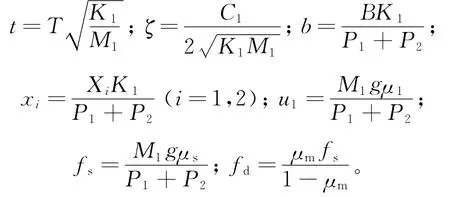
可將式（1）化為

2 系統的周期運動及穩定性

由于流的解析解很難給出，對于P這樣的映射一般借助數值方法來進行研究。通過映射P可以得到P的Jacobi矩陣DP，根據矩陣DP的特征值λi可以判斷圖1所示碰撞振動系統周期運動的穩定性和局部分岔［3－8］。

3 數值分析

在適當的參數下，振子的運動呈現周期性，并且圖1所示系統具有對稱性，在一定參數下系統會出現對稱的碰撞運動。假設在n個激勵周期內，經歷了p次右碰撞，q次左碰撞，k次黏滑后，系統運動重復，則稱為n－p－q－k運動。取系統的基本參數為：μm＝0.5，μk＝0.5，μc＝0.5，ζ＝0.1，v＝0.1，R＝0.8，f0＝1.0，以ω為控制參數分析摩擦力對系統分岔形式、黏滑和非黏滑碰撞的影響。

圖2為ω∈［2.5，13］時M1的分岔圖。首先分析u1＝0.1的情況（見圖2（a）），ω∈［11.955，13］時M1呈現出穩定的周期1－1－1－0對稱運動，ω∈（10.289，11.955）時M1呈現出穩定的周期1－1－1－0非對稱運動，ω＝10.289時M1呈現出穩定的周期2－2－2－0運動，同時隨著ω遞減為9.895，M1的運動將通過倍周期分化通向混沌，ω∈（8.736，9 .825）時M1呈現出穩定的周期1－2－1－0運動，ω＝8.736時M1呈現出穩定的周期2－4－2－0運動，同時隨著ω遞減為8.445，M1的運動也將通過倍周期分化通向混沌。

圖3為u1＝0.1時M1的黏滑及擦切圖。此時，M1在ω∈（6.162，8.736］區間內的黏滑運動不明顯，在ω∈［2.5，6.162］區間內的黏滑運動則比較明顯。ω∈［5.395，6.162］時M1呈現穩定的周期2－2－2－1運動（見圖3（a）），ω∈（4.532，4.732］時M1呈現穩定的周期1－3－2－1運動（見圖3（b）），ω＝4.532時M1呈現穩定的周期2－6－4－2運動，同時隨著ω遞減為4.450，M1的運動將通過倍周期分化通向混沌。ω∈［2.5，4.450）時M1呈現的黏滑現象更明顯，此時M1主要以倍周期分化通向混沌。

圖2 M 1的分岔圖Fig.2 Bifurcation diagram of M1

圖3 u1＝0.1時M 1的黏滑及擦切圖Fig.3 Stick－slip and brush cut diagram of M 1 when u1＝0.1

下面討論增大摩擦力（u1＝0.2）時的情況，此時M1的分岔圖見圖2（b），M1的黏滑及擦切圖見圖4。ω∈［7.5，13］時M1的黏滑運動不明顯，此時M1主要以倍周期分化通向混沌。ω∈［2.5，4.505］時M1不僅有明顯的黏滑運動，而且有擦切運動。ω∈（4.279，4.505］時M1呈現穩定的周期1－3－2－1運動（見圖4（a）），ω＝4.279時M1發生擦切運動（見圖4（b））。ω∈（4.145，4.279］時M1呈現穩定的周期1－4－2－1運動，當ω＝4.145或ω＝3.965時M1再次發生擦切運動（見圖4（c）），并最終通過擦切運動通向混沌。

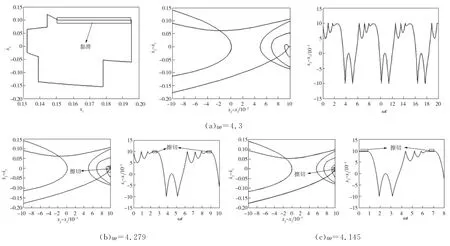
圖4 u1＝0.2時M1的黏滑及擦切圖Fig.4 Stick－slip and brush cut diagram of M 1 when u1＝0.2

減小摩擦力（u1＝0.01）時，M1的分岔圖見圖2（c），此時M1在ω∈2.5，］［13區間內的黏滑運動不明顯。

系統其他基本參數不變，當u1＝0.1時，M1在不同激勵振幅條件下的分岔行為如圖5所示。由圖5可見，在ω＝4.2的條件下，當f0＝0.1時，M1呈現穩定的周期1－2－3－0運動，當f0＝0.4時，M1呈現穩定的周期1－1－1－0運動，當f0＝0.95時，M1呈現穩定的周期1－3－2－1運動；在ω＝5.1的條件下，當f0＝0.1時，M1呈現穩定的周期2－4－4－0運動，當f0＝0.4時，M1呈現穩定的周期1－1－1－0運動，當f0＝0.95時，M1呈現穩定的周期2－4－4－2運動。

圖5 不同激勵振幅下M 1的分岔圖Fig.5 Bifurcation diagram of M1 under different incentive amplitudes

4 結論

（1）系統存在叉式分岔，并由對稱周期運動變為反對稱的周期運動，進而通過周期倍化分岔通向混沌。

（2）在一定的帶速下，系統主要以倍周期分岔為主，干摩擦較小時系統黏滑現象不明顯，而干摩擦較大、激勵頻率不太大時系統黏滑現象非常明顯，并且存在擦切運動。

（3）在一定帶速和干摩擦下，激勵振幅越大，系統越容易發生黏滑運動。對于此類系統，可以通過調整干摩擦和激勵振幅來抑制系統的黏滑現象。

［1］ Shaw S W.On the dynamic response of a system with dry friction［J］.Journal of Sound and Vibration，1986，108：305－325.

［2］ Cone K M，Zadoks R I.A numerical study of an impact oscillator with addition of dry friction［J］.Journal of Sound and Vibration，1995，188（5）：659－683.

［3］ Ding W C，Xie J H.Interaction of Hopf and doubling bifurcations of a vibro－impact system［J］.Journal of Sound and Vibration，2004，275（1－2）：29－45.

［4］ 丁旺才，張有強，謝建華.含對稱間隙的摩擦振子非線性動力學分析［J］.摩擦學學報，2008，28（2）：156－160.

［5］ 羅冠煒，張艷龍，謝建華.含對稱剛性約束振動系統的周期運動和分岔［J］.爆炸與沖擊，2007，4（7）：45－50.

［6］ 李萬祥，牛衛中.一類含間隙系統的分岔與混沌的形成過程［J］.振動與沖擊，2000，24（3）：48－49.

［7］ 羅冠煒，謝建華，孫訓方.兩自由度塑性碰撞振動系統的周期運動與穩定性［J］.蘭州大學學報，2000，36（3）：62－66.

［8］ 林梅，丁旺才，武俊虎.兩點碰撞振動系統的周期運動與分岔［J］.動力學與控制學報，2000，4（1）：17－21.