一維p－ Laplace方程解的整體分支結構

胡 松

（武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北武漢，430065）

本文主要研究一維p－Laplace算子

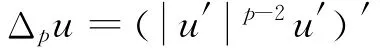
在Dirichlet邊值條件下的整體分支現象。

任取p∈1，＋（）∞，考慮如下非線性特征值問題：

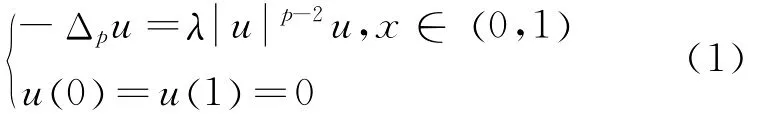
接著討論如下邊值問題：

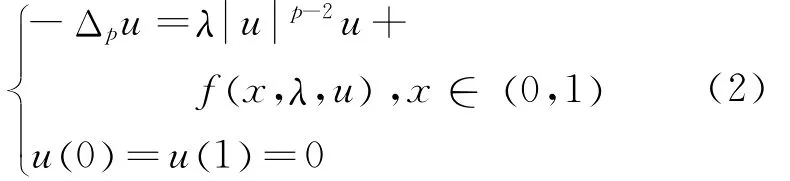
其中，函數f（x，λ，u）表示式（2）的高階項，且滿足適當的增長性條件。利用Leray－Schauder度理論可以證明（λn（p），0）是式（2）的一個分支點，進而根據文獻［1］中的標準分支定理得到關于式（2）解的整體分支結構。

分支理論自提出后已經被應用到很多具體問題中。Del Pino等［2］證明了Dirichlet邊值條件下p－Laplace算子的第一特征值λ1（p）是單重的、孤立的，且（λ1（p），0）為一個分支點，進而給出了在（λ1（p），0）處解的整體分支結構。趙昆等［3］將上述結果推廣至加權p－Laplace算子中。Drabek等［4］證明了Navier邊值條件下p－biharmonic算子的第一特征值λ1（p）是單重的、孤立的，且（λ1（p），0）為一個分支點，進而給出了在（λ1（p），0）處解的整體分支結構，并進一步證明了當N＝1，Ω＝（0，1）時，p－biharmonic算子存在有無窮多個特征值λn（p）（n＝1，2，…，∞），每一個特征值都是單重的、孤立的且（λn（p），0）都為分支點，進而給出在（λn（p），0）處解的整體分支結構。本文作者將上述結果推廣至加權p－biharmonic算子中［5－6］。Benedikt［7］利用文獻［4］的思想證明了當N＝1，Ω＝（0，1）時，Dirichlet和Neumann邊值條件下p－biharmonic算子存在有無窮多個特征值λn（p）（n＝1，2，…，∞），每一個特征值都是單重的、孤立的且（λn（p），0）都為分支點，進而給出了在（λn（p），0）處解的整體分支結構。Evans［8］討論了當p＝2時，Dirichlet邊值條件下Laplace算子特征值的存在性及其相關性質。

本文在此基礎之上，利用文獻［4］的方法討論了當N＝1、Ω＝（0，1）時，Dirichlet邊值條件下p－Laplace算子特征值的存在性及其相關性質，進而給出了在分支點處解的整體分支結構。

本文主要結果敘述如下：

每一個特征值λn（p）都是單重的、孤立的，且λn（p）作為p的函數都是連續的。

定理2 假設p＞1，函數f（x，λ，s）表示式（2）的高階項，且滿足適當的增長性條件，即對任意給定的有界區間J?R，存在指數q∈（p，p＊＊），使得對任意的ε＞0，總存在常數Cε＞0，滿足

則問題（2）的所有非平凡解構成的解空間Γ的閉包中包含一個極大子閉聯集Υ，且滿足

（i）閉聯集Υ在中無界，或者

1 輔助性結果

引理1 問題（1）存在著一個最小的、正的特征值λ＝λ1（p），且λ1（p）是單重的、孤立的。問題（1）相對于特征值λ1（p）的特征函數u1（p）是嚴格正的。更進一步，問題（1）存在正解的充要條件為λ＝λ1（p），λ1（p）作為p的函數是連續的。

注：引理1的證明見文獻［2］和文獻［3］。

引理2 假設（u，ω）滿足如下方程：

則問題（3）的解（u，ω）是局部惟一的。其中φp（s）

注：引理2的證明見文獻［4］。

引理3 假設A是緊線性算子且不以1為特征值，所有大于1的特征值的重數和為γ，則Deg其中Br（0）表示以原點為球心，r為半徑的球體。

注：引理3的證明見文獻［9］。

2 特征值問題

假設λ＝λ1（p），其中λ1（p）是問題（1）的最小特征值，且u＝u1（x）為相對于特征值λ1（p）的特征函數。當n＞1時，定義

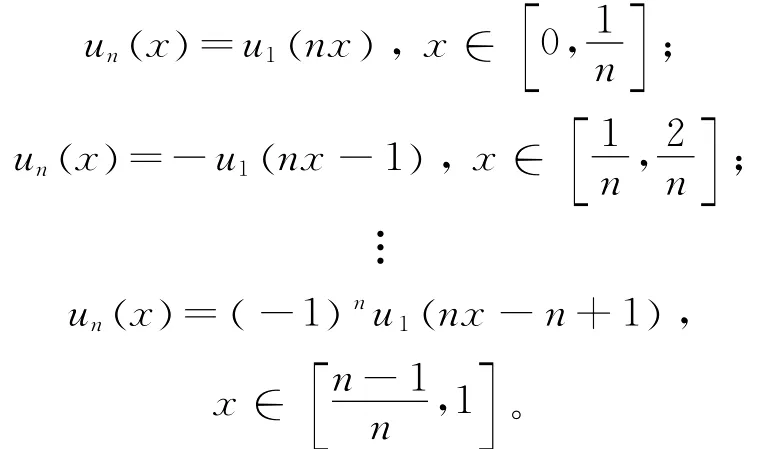
證明 假設u＝u（x）為當λ＝λn（p）（n＞1）時的任一特征函數，則由引理1易知u＝u（x）在（0，1）上是變號的。顯然，當λ＝λn（p）時，u＝u（x）滿足方程（3）。假設，則ω（0）＝u（0）＝0。由引理2可知u（x）≡0。這與u＝u（x）在（0，1）上是變號的相矛盾。故因為，故可引入伸縮變換，使得又因u（0）＝un（0）＝0，且當λ＝λn（p）時，u＝u（x）和u＝un（x）均滿足方程（3），故由引理2可知u（x）≡un（x），x∈［0，1］，證畢。

證明 假設存在λ＝λe≠λn（p）（n≥1），且λ＝λe為問題（1）的特征值，定義

綜上所述，結合引理1、引理4、引理5及引理6的結果很容易得到定理1的結論。

3 整體分支結果

首先考慮如下輔助問題：

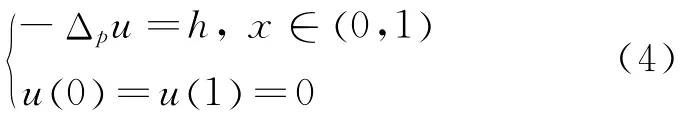
取Ω＝（0，1），設稱u∈為問題（4）的弱解，如果對任意的φ∈，有其中表示之間的對偶積。

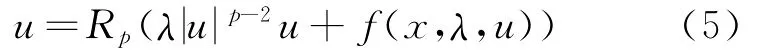
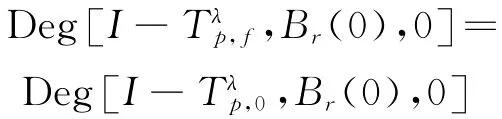
證明

（i）假設p＜2，定義λ（q），q∈p，［］

2滿足

易驗證A為緊線性算子。假設λ＊為A的任一特征值，則Au＝λ＊u。即R2（λ（2）u）＝λ＊u。故對任意的有即又因λ（2）＜λ（2）＜λ（2），故nn＋1λ＊≠1。即A滿足引理3的條件。由上述分析可知，要使A有特征值λ＊，只需即可。假設λ＊＞1，則即k＝1，2，…，n，有λ＊的重數γ＝n。故由定理1及引理3可知結論成立，證畢。

綜上所述，結合引理7、引理8及文獻［1］中標準分支定理很容易得到定理2的結論。

［1］ Rabinowitz P H.Some global results for nonlinear eigenvalue problems［J］.J Funct Anal，1971（7）：487－513.

［2］ Del Pino M，Manasevich R.Global bifurcation from the eigenvalues of thep－Laplacian［J］.J Diff Equations，1991，92（2）：226－251.

［3］ 趙昆，陳祖墀.加權p－Laplacian方程解的整體分叉問題［J］.數學物理學報，2005，25A（2）：145－157.

［4］ Drabek P，Otani M.Global bifurcation result for thep－biharmonic operator［J］.Electronic Journal of Differential Equations，2001，48：1－19.

［5］ 胡松.加權p－harmonic方程的非線性特征值問題［J］.華中師范大學學報：自然科學版，2008（3）：1－5.

［6］ 胡松.加權p－harmonic方程解的整體分支結構［J］.華中師范大學學報：自然科學版，2009，43（1）：14－18.

［7］Benedikt J.Global bifurcation result for Dirichlet and Neumannp－biharmonic problem［J］.Nonlinear Differential Equations and Applications，2007（14）：541－558.

［8］Evans L C.Partial differential equations［M］.Rhode Island：American Mathematical Society，1998.

［9］ 葉其孝，李正元.反應擴散方程引論［M］.北京：科學出版社，1999.