改進BP神經網絡模型及其穩定性分析

張國翊，胡錚

（北京郵電大學 泛網無線通信教育部重點實驗室，北京，100876）

改進BP神經網絡模型及其穩定性分析

張國翊，胡錚

（北京郵電大學 泛網無線通信教育部重點實驗室，北京，100876）

針對傳統BP算法抗干擾能力差、學習速率慢且易陷入局部極小點等缺點，提出一種基于變更傳遞函數傾斜度和動態調節不同學習速率的BP改進算法，并在此基礎上采用Lyapunov穩定性原理分析改進算法的收斂性。該算法綜合考慮網絡訓練方式和學習率的不足，設計新的復合誤差函數，同時采用一種分層動態調整不同學習率的新方法，并采用批量樣本進行訓練，以加快傳統BP算法的收斂速度和避免陷入局部極小值點。在此基礎上，將該算法應用于帶鋼表面缺陷圖像檢測中，并比較改進算法與傳統算法在缺陷檢測中的性能參數。研究結果表明：該改進算法能夠提高缺陷識別率，檢測速度快，更能滿足鋼板表面質量檢測的實時性要求，是一種行之有效的方法。

BP神經網絡；缺陷檢測；復合誤差函數；Lyapunov穩定性

未來的通信網絡將是一個泛在、異構的網絡模式，需要能夠實時感知周圍的網絡環境，通過對所處環境的理解，實時調整通信網絡的配置，智能地適應所處環境的變化，同時它還具備從變化中學習的能力，且能用于未來的決策中。在這種情況下，尋找一種能夠實時感知網絡環境變化，實現網絡對環境自適應的方法就顯得尤為重要。人工神經網絡理論作為一門新興學科，近年來被廣泛應用于通信領域（如網絡自配置、自優化與自管理）和工業領域（如缺陷識別與分類）中，其所具有的實時性、容錯性和學習性等特征為各領域問題的解決提供了有效的理論和技術支撐。然而，目前，普遍采用基于誤差逆傳播的BP學習算法，主要存在2個問題，即收斂速度慢和易陷入局部極小。從神經網絡在模式識別中的發展來看，大型網絡結構的優化問題和網絡學習問題還亟待進一步解決和提高[1?2]。目前網絡模型的改進主要包括網絡結構和學習算法改進2個方面。BP網絡結構的改進主要在互連方式、轉換函數以及隱含層節點等方面，而算法改進主要通過修改誤差函數、增大激勵函數的導數以及與其他智能算法相結合等來提高網絡性能。在此，本文作者主要通過構造了復合誤差函數來避免局部極小，同時采用一種分層調整不同學習率的新方法來加快收斂速度，提出一種新的學習算法，并在此基礎上采用Lyapunov穩定性原理分析改進算法的收斂性。

1 傳統BP算法

這里，以3層BP網絡為例。假設輸入層、隱含層和輸出層的神經元個數分別為N，M和L，對應任意輸入樣本向量為實際輸出向量為期望輸出向量為輸入層到隱含層的連接權值為wij（1≤i≤N, 1≤j≤M），隱含層至輸出層的連接權值為vjt（1≤j≤M, 1≤t≤L），隱含層各單元的輸出閾值為jθ（1≤j≤M），輸出層各單元的輸出閾值為tγ（1≤t≤L），g（x）和f（x）分別為隱含層和輸出層的傳遞函數。設m為訓練網絡的迭代次數，連接權值和實際輸出都是m的函數。

用第k個輸入樣本連接權值wij和閾值jθ計算隱含層各神經元的輸入，然后，用通過g（x）傳遞函數計算隱含層各神經元的輸出

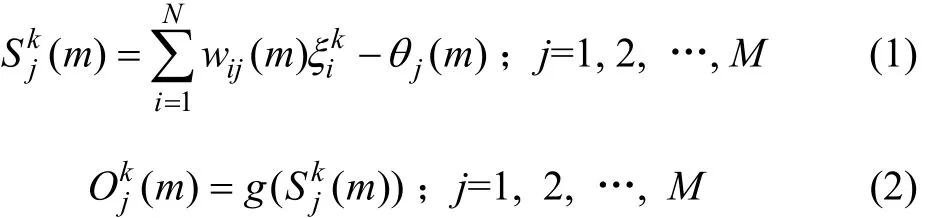
同樣，用隱含層的輸出、連接權值vjt和閾值γt計算輸出層各神經元的輸入，然后，用通過f（x）傳遞函數計算輸出層各神經元的響應：

對于傳統BP算法，通常選擇以Sigmoid型函數作為輸出層和隱含層的傳遞函數，即

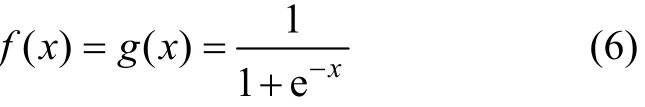
從優化理論上來說，BP算法是一種梯度下降法，傳統BP算法中的學習率就是梯度下降法的步長。BP算法中網絡參數每次調節的幅度，均以一個與網絡誤差函數成正比的學習率η進行。在傳統BP算法中，無論是在隱含層還是在輸出層，在其連接權值和閾值參數的修正過程中，學習率η總是固定不變的[1?2]。

2 傳統BP算法的不足

在實際應用中，傳統BP算法主要存在以下幾個不足[2?3]：

（1） 學習算法的收斂速度比較慢。在處理圖像缺陷在線檢測這樣一個比較復雜的問題時，由于系統實時性要求很高，這就要求學習算法的收斂速度要更快。

（2） 易陷入局部極小值。BP網絡采用梯度下降法，訓練是從某一起始點開始的斜面逐漸達到誤差的最小值。對于復雜網絡，其誤差函數為多維空間的曲面，因而在其訓練過程中，可能陷入某一局部極小值。雖然傳統算法在權值更新時增加了新的沖量項以避免陷入局部極小值，但效果并不明顯。

（3） 網絡隱含層的層數以及隱含層神經元數的選取尚無理論指導，而是根據經驗選取，因此，網絡往往有很大的冗余性，也增加了網絡學習的時間。

（4） 網絡的學習、記憶具有不穩定性，新加入的樣本會影響到已學完的樣本。

3 新的BP改進算法

3.1 網絡訓練方式及傳遞函數的改進

在冷軋帶鋼表面缺陷檢測系統中，由于訓練網絡時的樣本數量較多，而且具有一定數量的重復樣本，所以，在BP改進算法中，嘗試采用分組批處理的訓練方式，即假設先把所有P個訓練樣本分為n組，每組的樣本數為Pi（1≤i≤n），然后對Pi個樣本進行網絡訓練，讓每組樣本循環經過1次學習后再調整學習率，而不是每輸入1個樣本就調整1次學習率。采用分組批處理方式訓練網絡的優點是：既能使不同學習率在每組樣本圖像循環訓練完成后得到適當調整，又能減小調整學習率的時間。因此，分組批處理的訓練方式中，對于各分組Pi（1≤i≤n）個訓練樣本，神經網絡實際輸出值（）與理想輸出值（）間的全局均方誤差函數表示為：

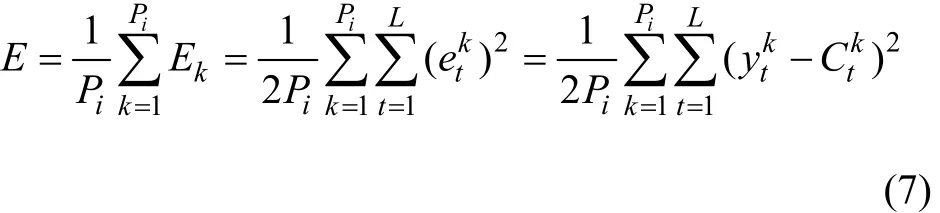
同時，對于新的BP改進算法，這里選擇以α為傾斜度參數的雙曲正切S型函數作為隱含層的傳遞函數，即

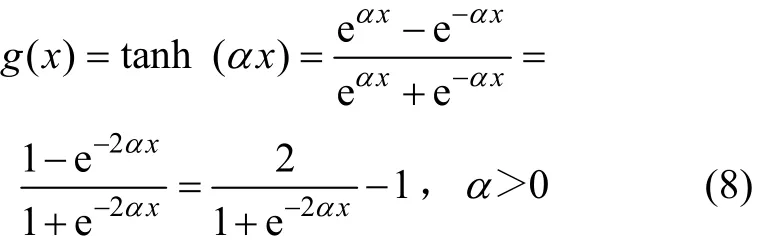
該傳遞函數是以α為傾斜度參數的單調遞增的有界函數，它的基本特性包括：

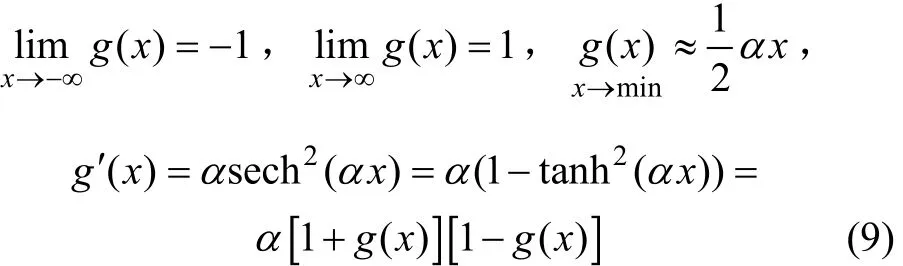
圖1所示為傾斜度參數α取5，3，1和0.5這4個不同值時的傳遞函數g（x）=tanh（αx）曲線；圖2所示為用線性逼近傳遞函數時的誤差率。

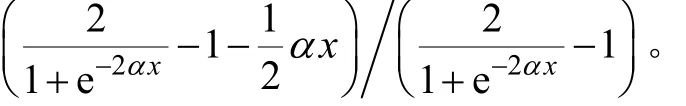
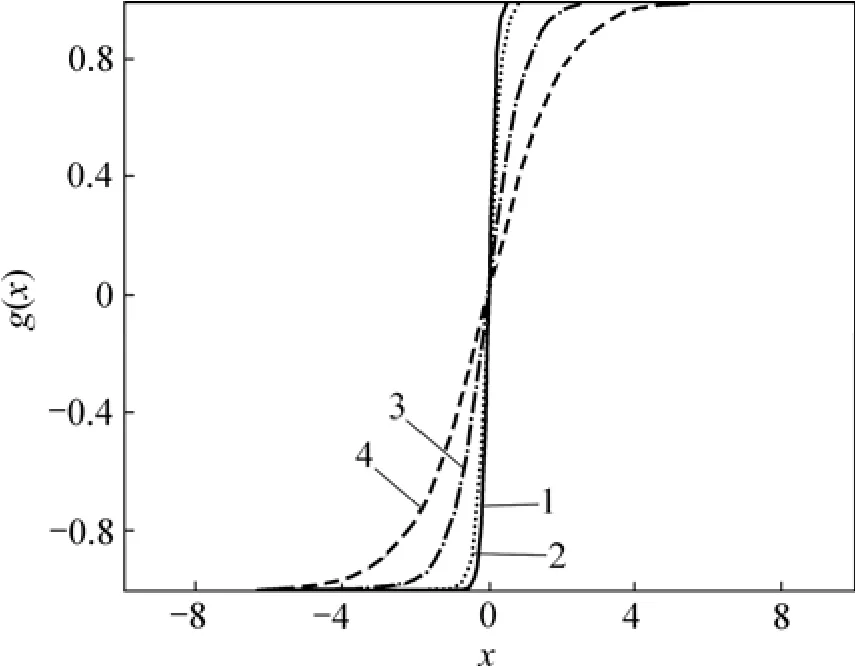
圖1 傳遞函數曲線Fig.1 Transfer function curves

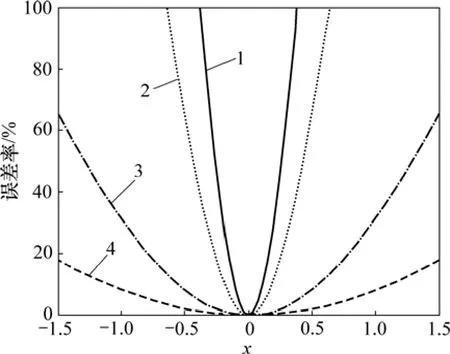
圖2 線性逼近傳遞函數的誤差率Fig.2 Error rate of linear approximation transfer function

3.2 復合誤差函數的設計

BP算法本質上是以誤差平方和函數為目標函數，用梯度下降法求其最小值的算法。在訓練樣本的初始階段，輸出值遠離期望值，E相對較大，ΔE有較大的下降空間，所以，E對加快網絡的收斂速度有較大的貢獻；隨著訓練樣本以及訓練次數的逐漸增加，輸出值逐漸靠近期望值，E不斷減小，ΔE的下降空間也不斷縮小，此時，網絡的收斂速度將變得非常緩慢。同時，由于全局均方誤差函數E是一個非線性函數，意味著由E構成的連接空間不是只有1個極小點的拋物面，而是存在多個局部極小點的超曲面，因此，誤差逆傳播網絡的收斂過程很可能進入局部極小點，而無法最終收斂到全局最小點。導致這一缺陷的原因是BP學習規則采用了按誤差函數梯度下降方向進行收斂[3,6?7]。為此，本文構造了復合誤差函數G（m）λ=來代替傳統算法中的全局均方誤差函數E（m）。復合誤差函數的具體展開式為：

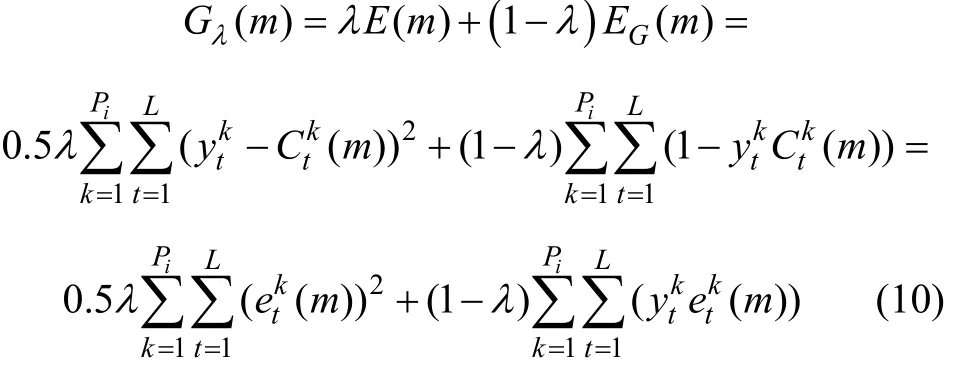
在訓練樣本的初始階段網絡的實際輸出與期望輸出相差較大，λ=1，此時Gλ（m）=E（m），即為全局均方誤差函數，網絡收斂速度加快；隨著訓練樣本以及訓練次數的逐漸增加，E不斷減小，當λ從1趨向于0時，（1-λ）EG（m）部分貢獻值增大，此時，Gλ（m）=EG（m），網絡收斂速度同樣加快，這在一定程度上克服了傳統BP算法收斂速度慢的缺點。對于函數G（m）收斂性，當ek（m）→0時，復合誤差函數λt能使E（m）和EG（m）同時達到極小，收斂性與E（m）的收斂性是一致的。

3.3 分層動態調節不同學習速率

BP算法中網絡參數每次調節的幅度均以1個與網絡誤差函數成正比的學習率η進行。在傳統BP算法中，無論是在隱含層還是在輸出層，在其連接權值和閾值參數的修正過程中，學習率η總是固定不變的。其原因是誤差函數E是一個復雜的非線性函數，很難通過求極小值的方法得到最佳步長η。在誤差曲面較平坦處，連接權值和閾值參數的調節幅度較小，以致需要經過多次調整才能將誤差函數曲面降低；而在誤差曲面較陡處，連接權值和閾值參數的調節幅度較大，誤差函數在最小點附近將發生過沖現象，使得權值參數調節路徑呈現鋸齒形，難以收斂到最小值點。這也是傳統BP算法收斂速度慢的一個重要原因[5,8]。

本文采用一種分層動態調整不同學習率的新方法，即分開調整輸出層學習率η1和隱含層學習率η2，從而替代了傳統算法中固定不變的學習率η。根據Delta學習規則，隱含層至輸出層的連接權值vjt和輸入層到隱含層的連接權值wij的修正量分別為：

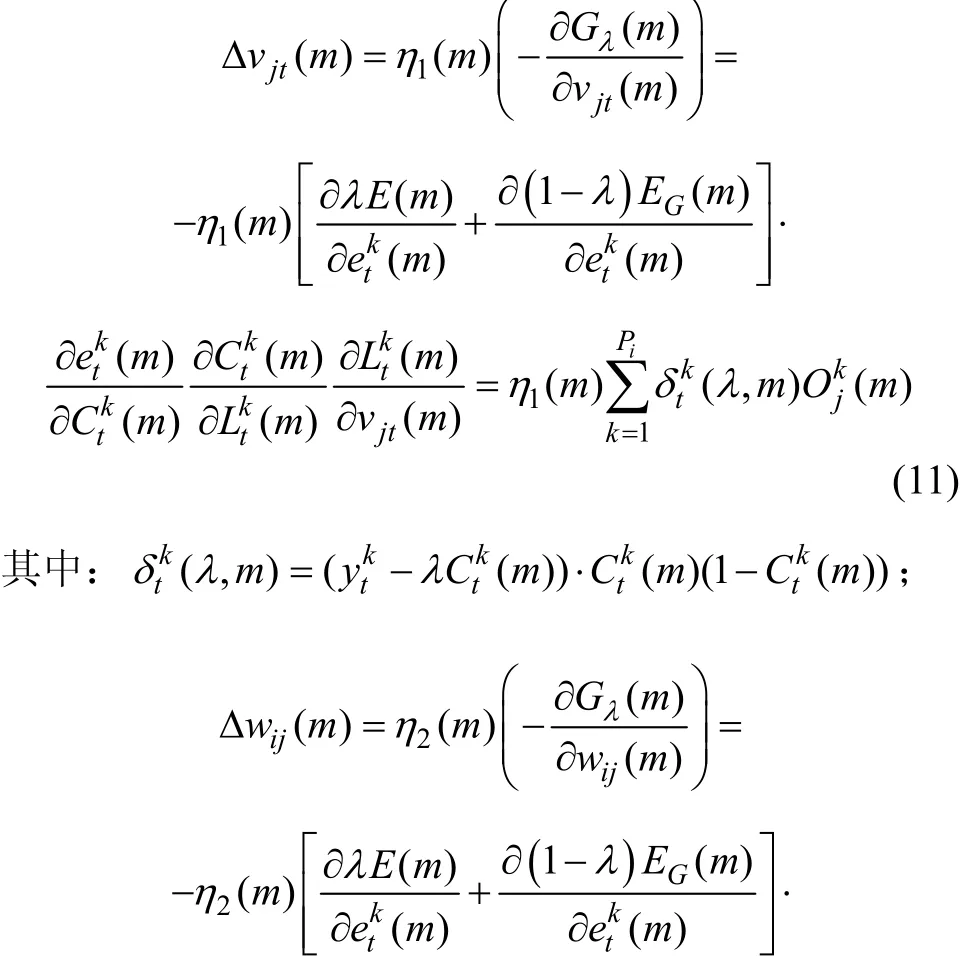
式中：η1（m+1）是分組樣本在第m+1次循環學習時輸出層的學習率；η2（m+1）是分組樣本在第m+1次循環學習時隱含層的學習率；ΔE（m）/E（m）為分組樣本在第m次循環學習時的組內均方誤差變化率；τ為常數，取值范圍為0＜τ＜1，這里統一取τ=0.5。

采用誤差學習率作為修正參數的原因是：當ΔE（m）＞0時，說明學習誤差增大，輸出值遠離期望值，權值調整過大，需要減小Δvjt（m）和Δwij（m）。由式（11）和式（12）可知：若降低學習率η1和η2，Δvjt（m）和Δwij（m）也必然減小。同時由式（13）可以看出：η1（m+1）＜η1（m），η2（m+1）＜η2（m），η1和η2減小，故能加快網絡收斂速度；當ΔE＜0時，說明學習誤差減小，輸出值靠近期望值，需要增大Δvjt和Δwij。但此時誤差已經很小，ΔE的變化也小，收斂速度很慢，但ΔE/E比ΔE要大得多，因此，從式（13）可以看出，η1（m+1）＞η1（m），η2（m+1）＞η2（m），η1和η2明顯增大，同樣也能加快網絡收斂速度[9]。

因此，BP改進算法中輸出層和隱含層各神經元的連接權值vjt和wij修正公式分別為：

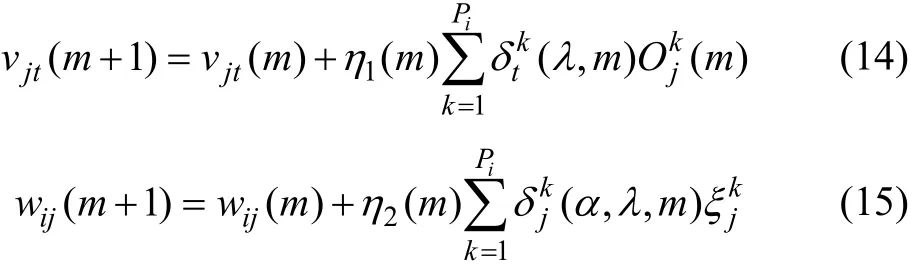
3.4 BP改進算法穩定性分析

學習率的選擇對神經網絡的運行性能至關重要，學習率太小會使網絡收斂太慢，學習率太大則會使網絡的運行不穩定。為了高效地訓練神經網絡，從離散型的Lyapunov穩定性方法出發，以BP改進算法為例，給出保證神經網絡穩定性的自適應學習率[10?11]。

結論1：若η1（m）滿足：

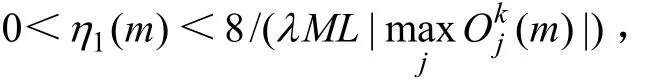
則由上述學習算法所表達的對權值vjt（m）的迭代學習過程穩定收斂。

結論2：若η2（m）滿足：

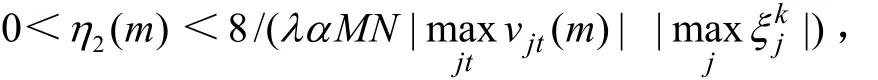
則由上述學習算法所表達的對權值wij（m）的迭代學習過程穩定收斂。

首先證明結論1。

定義Lyapunov能量函數與傳統誤差函數類似，其表達式為：

其中：

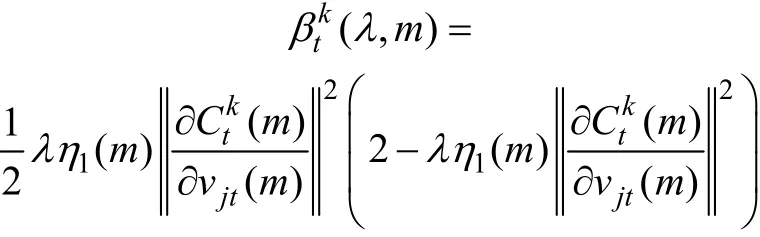
這里把vjt（m）看成1個M×L維度向量。注意到BP改進算法中，選擇Sigmoid函數作為輸出層的傳遞函數，即f（x）=1/（1+e-x），而0＜f′（x）≤1/4，所以，

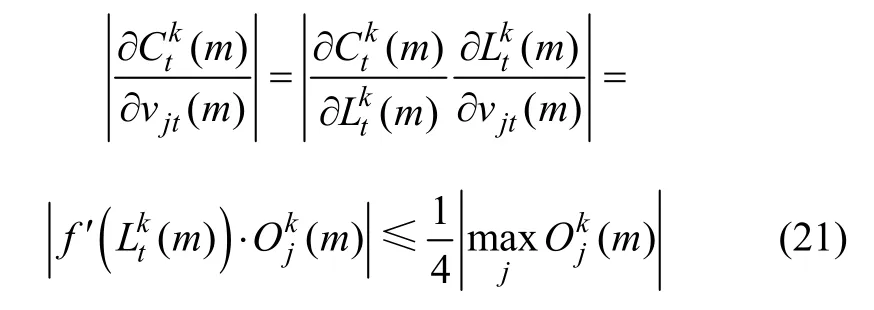
按照歐氏范數的定義，有：

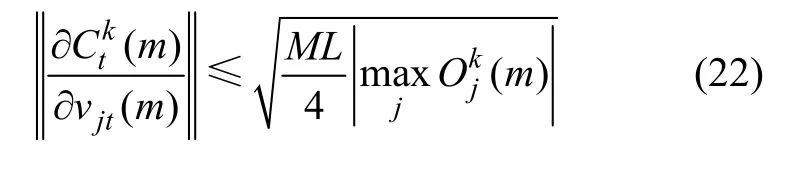
同理可以證明結論2。

由上述定理的結論可知：當η1（m）滿足0＜可保證網絡訓練收斂。但當達到最小，即網絡能以最快速度收斂。若近似認為，則取η1（m）=，可以保證網絡以較快速度收斂。同理，可取以保證網絡較快收斂。

4 缺陷檢測試驗及分析

4.1 算法描述

基于上述分析，采用BP改進算法進行缺陷檢測程序的具體實現步驟如下。

（1） 初始化連接權值（wij和vjt）、閾值（θj和γt）、學習率（η1和η2）和傳遞函數傾斜度參數α。假設把所有P個訓練樣本分為n組，每組的樣本數為Pi（1≤i≤n），設定組內期望誤差標準ε以及最大循環迭代次數M。設為組內第m次迭代時網絡的實際輸出量，為組內期望輸出量，m為循環迭代次數，令m=0。

（3） 對輸入樣本kξ，按式（1）和（3）分別計算隱含層和輸出層的輸入值；按式（2）和（4）分別計算隱含層和輸出層的輸出值。其中隱含層的傳遞函數選擇以α為傾斜度參數的雙曲正切S型函數g（x）=輸出層的傳遞函數選擇常見的Sigmoid型函數f（x）=1/（1+e-x）。

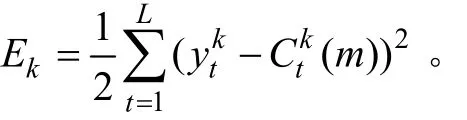
（5） 判斷循環學習次數m是否大于最大循環迭代次數M，若是，則轉至（9），否則判斷該組訓練樣本的第m次循環迭代的全局均方誤差|E（m）|是否小于期望誤差標準ε；或者判斷連接權值的變化是否已經很小，即|vjt（m+1）?vjt（m）|＜ε，|wij（m+1）?wij（m）|＜ε，若是，則轉至（7），否則轉至（6）。

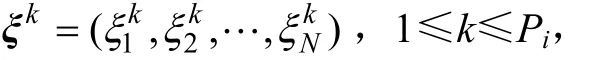
（7） 對于同組訓練樣本，在學習率（η1（m）和η2（m））不變的條件下，判斷α改變次數是否超過3次，若是，則轉至（8）；否則，適當改變傳遞函數傾斜度α，并重新返回（2）。

（8） 比較相同學習率（η1（m）和η2（m））和不同α參數值條件下，該組訓練樣本全局均方誤差E，得出使該組樣本均方誤差最小時的α。

（9） 算法結束。

BP改進算法流程如圖3所示。

4.2 訓練樣本選擇與獲取

試驗中選取帶鋼常見的6種表面缺陷樣本圖像訓練網絡，包括壓痕、氧化色、擦傷、飛邊、孔洞和輥印。訓練樣本圖像的獲取方式如下：專業質檢人員對現場采集的冷軋帶鋼樣本圖像的缺陷圖像和標準圖像進行集中標定后，從中挑選出750張典型的、能代表各類缺陷的樣本圖像作為訓練樣本圖像，其中絕大部分都是本文所涉及的常見的幾種缺陷類型，但缺陷圖像質量以及缺陷部分的方位不盡相同，如：由于攝像機現場受外界干擾導致拍攝圖像放大或縮小比例不同，使得缺陷部分清晰度不一樣；由于冷軋機器設備等原因造成同類缺陷的缺陷方向或位置不一致，訓練圖像是經過水平旋轉不同度數如45°，90°，135°或180°形成的。值得提出的是：由于冷軋帶鋼生產現場環境很復雜，存在著各種各樣干擾和噪聲，所以，采集得到的冷軋帶鋼樣本圖像難免有不同程度的失真現象，這就要求系統在提取樣本圖像特征向量之前先進行圖像的預處理工作（去噪、濾波），否則容易引起系統誤檢，從而得出錯誤的結論。

4.3 試驗結果分析

冷軋帶鋼表面缺陷檢測系統中采用以上BP改進算法，網絡仍采用3層結構檢測方式采用樣本圖像內任意區域的實時在線檢測方法，即對于樣本圖像中有缺陷的部分，用任意矩形框將該區域框起來后，對該矩形框區域內的所有像素點從右到左、從下到上進行掃描，計算出各像素點的灰度，并提取該矩形框區域內圖像的NMI特征[12]、低階不變矩（M1，M2，M3和M4）特征，矩形框區域所有像素點的灰度平均值和灰度方差總共7個特征量作為缺陷圖像的特征矢量，并將上述特征矢量作為網絡的輸入，隱含層設有15個神經元，隨機初始權值和初始閾值范圍均為?0.5～0.5，期望誤差標準ε=0.000 5，最大迭代次數設為2 000。

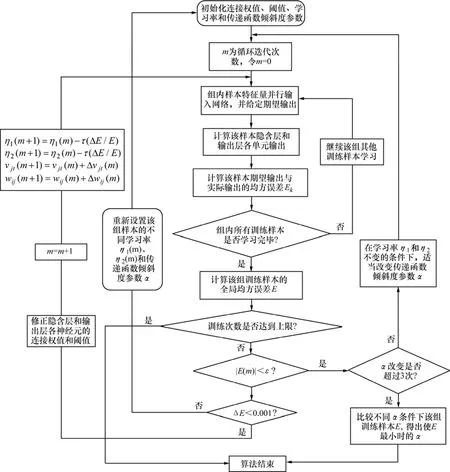
圖3 BP改進算法流程圖Fig.3 Flow chart of improved BP algorithm

同時，考慮到帶鋼表面質量檢測時，有可能出現誤判，因此，只簡單考慮網絡的輸出響應為“有缺陷”（0, 0）和“無缺陷”（1, 1） 2種情況，所以，輸出層神經元數目為2。系統中選擇隱含層的傳遞函數為傾斜度參數α的雙曲正切S型函數g（x），輸出層的傳遞函數為常見的Sigmoid型函數f（x）。為避免學習算法不收斂，提高學習速度，設期望輸出為相應小數，即（0.000 1, 0.000 1）判為“有缺陷”，（0.999 9, 0.999 9）判為“無缺陷”。

在缺陷檢測試驗中，首先把挑選出來的750個訓練樣本分成10組，前4組每組樣本數為90，后6組每組樣本數為65。對于各組樣本，在學習率η1和η2一定的條件下，比較3個不同傾斜度參數α所對應的組內全局均方誤差，其中中間α所對應的組內全局均方誤差最小，具體實驗結果如表1所示。從表1可以看出：對于數量較多的訓練樣本組，在學習率η1和η2一定的條件下，傾斜度參數α不同取值所對應的組內全局均方誤差相差較大；而對于數量較少的訓練樣本組，在學習率η1和η2一定的條件下，傾斜度參數α不同取值所對應的組內全局均方誤差相差較小。

為研究傾斜度參數α取不同值時對BP改進算法收斂情況以及各組組內均方誤差的影響，從表1的10組訓練樣本中分別選取第1，3，6和9組進行BP網絡訓練仿真實驗，仿真結果如圖4所示。其中：第1和3組每組樣本數為90，第6和9組每組樣本數為65。對于各組訓練樣本，在學習率η1和η2一定的條件下，比較傾斜度參數α取3個不同值時所對應的組內均方誤差和訓練次數。從圖4可以看出：當α取中間值時，BP改進算法收斂速度最快，網絡在250～350步之間就收斂，并且此時所對應的組內全局均方誤差能達到最小值，即α取中間值的點劃線總是位于仿真圖的下方；因此，根據圖4訓練次數和均方誤差，同樣可確定每組訓練樣本中α的最佳值。從圖4還可以看出：對于數量較多的第1和3組訓練樣本，在學習率η1和η2一定的條件下，α不同取值所對應的組內均方誤差相差較大；而對于數量較少的第6和9組訓練樣本，在學習率η1和η2一定的條件下，α不同取值所對應的組內均方誤差相差較小。

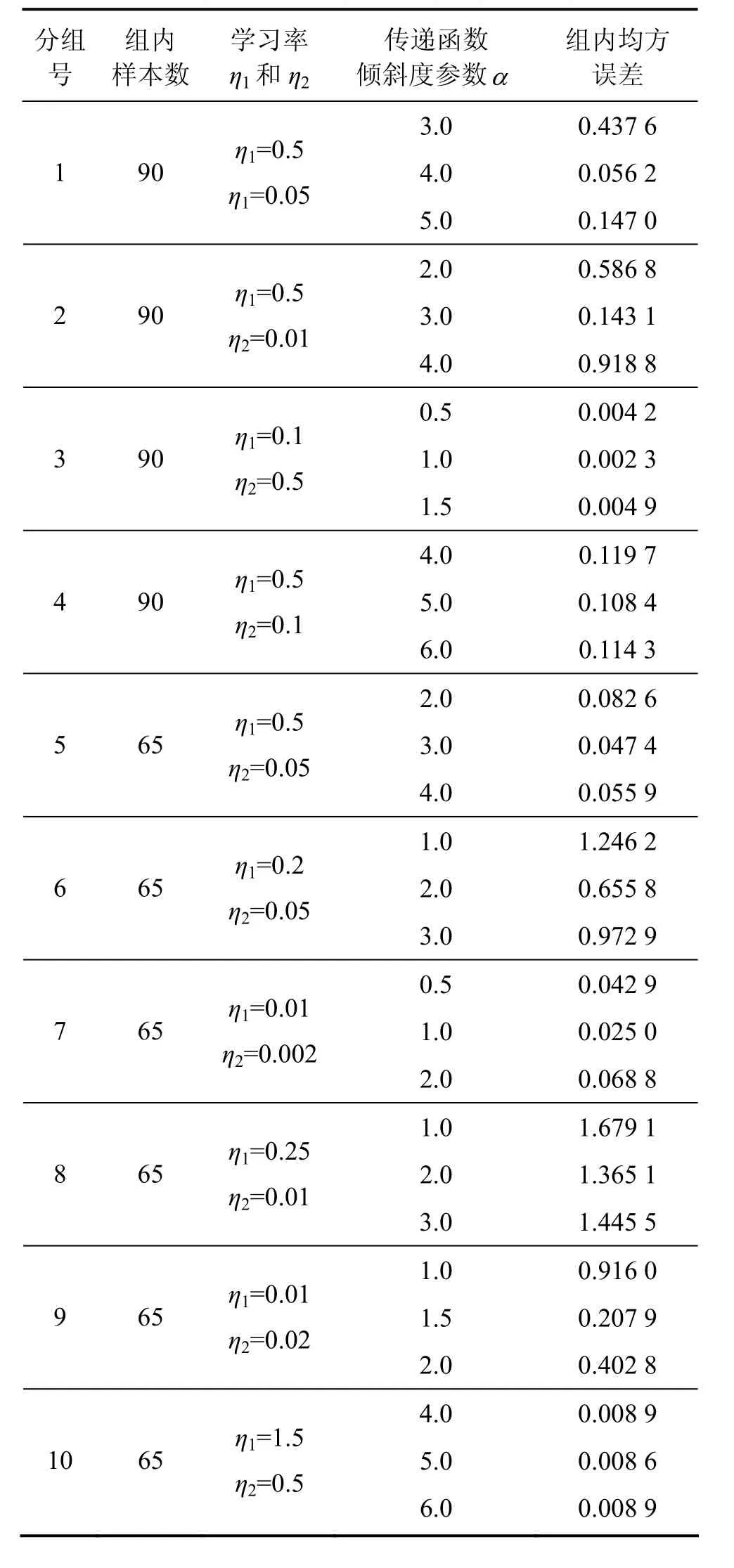
表1 BP改進算法分組訓練實驗結果Table 1 Improved BP algorithm group training results

4.4 算法性能比較

為了便于分組比較傳統算法和改進算法的性能，從現場采集的冷軋帶鋼缺陷圖像中同樣選取750個測試樣本進行組內全局均方誤差的計算。考慮到現場采集情況復雜，這750個測試樣本不免與表1中分組訓練網絡的學習樣本有較大重復，在計算BP改進算法的組內全局均方誤差時，可以采用表1中各分組的最佳參數值，具體分組測試實驗結果如表2所示。

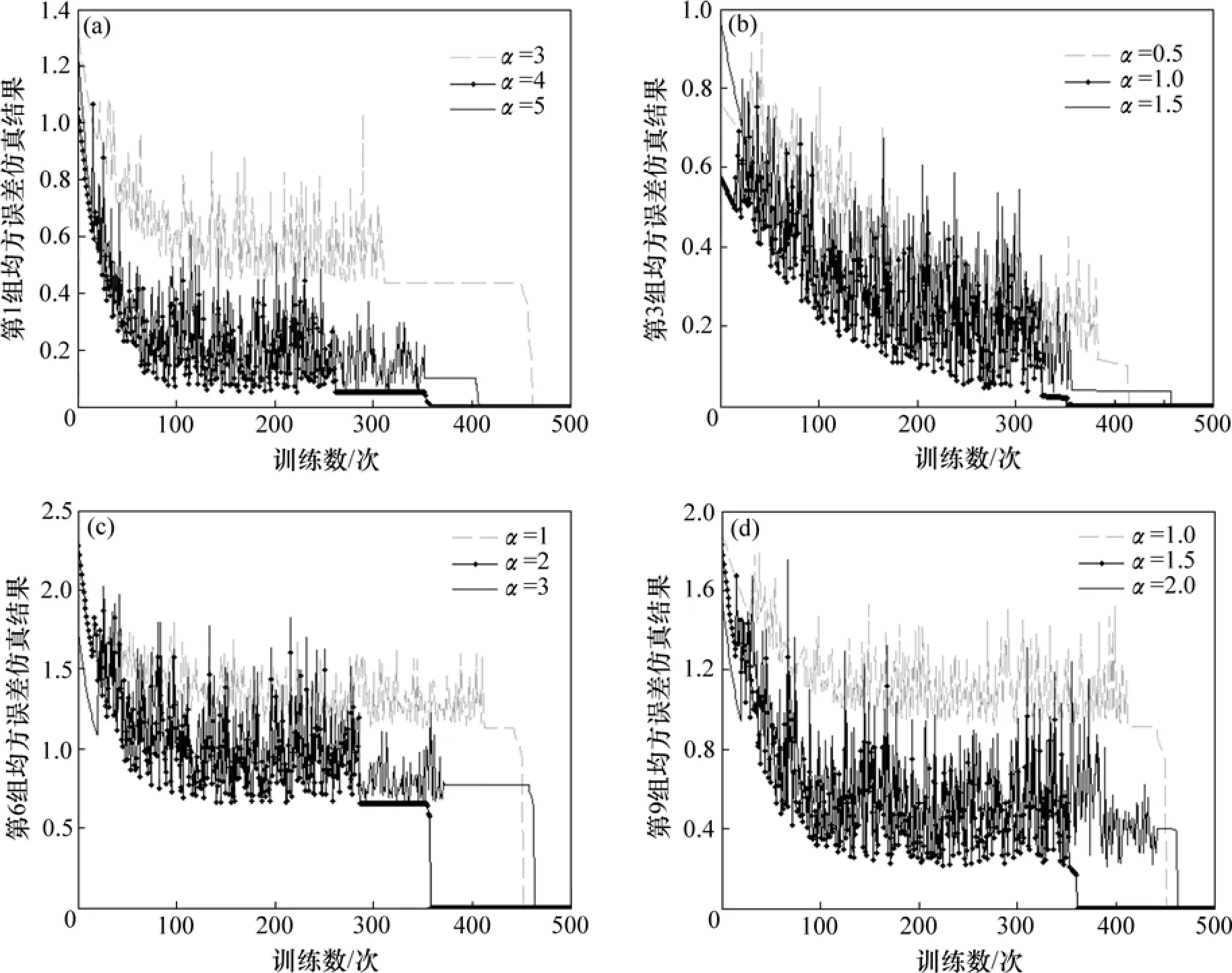
圖4 BP改進算法分組網絡訓練仿真結果Fig.4 Simulation results for improved BP algorithm group training

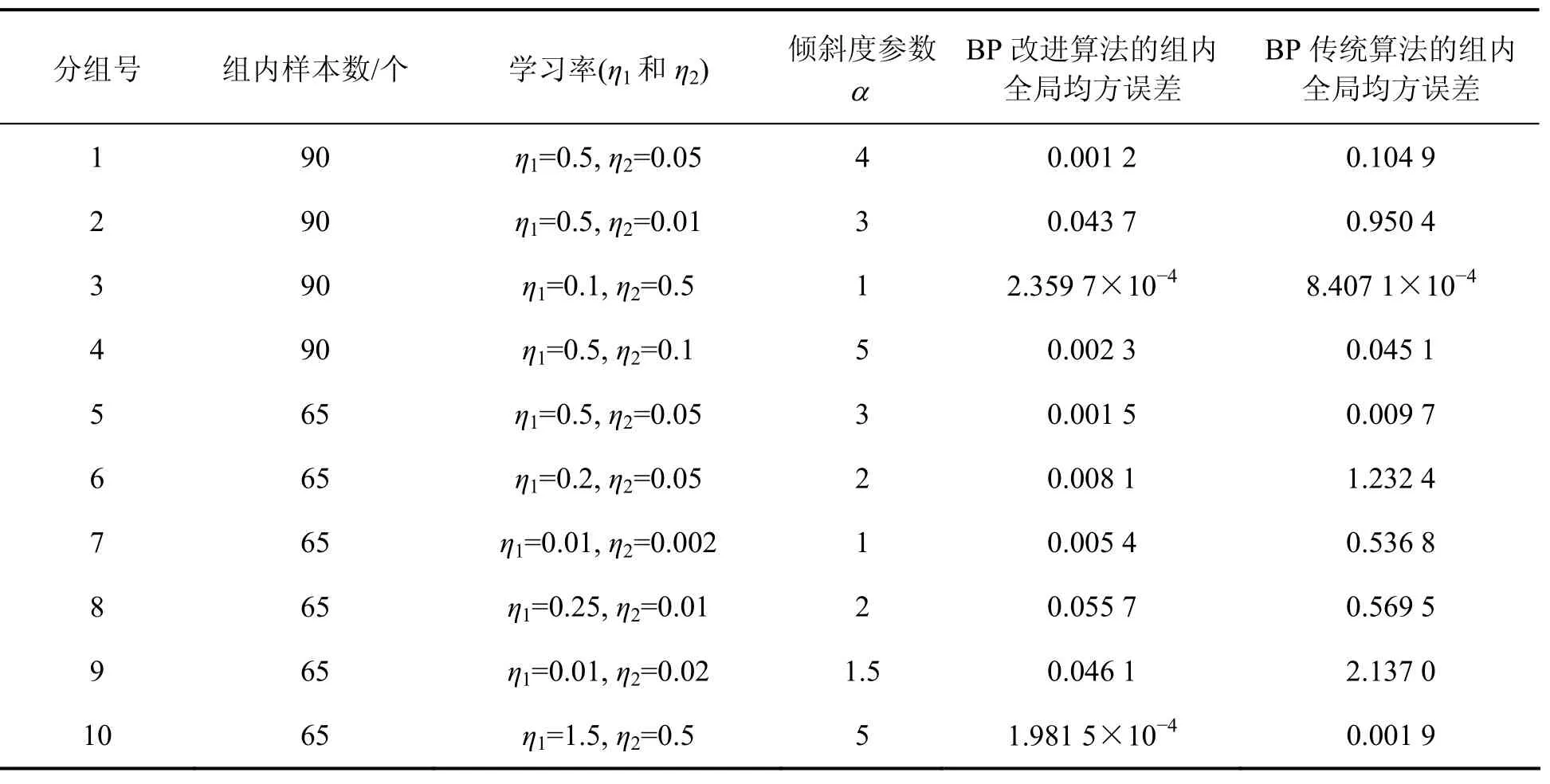
表2 BP傳統算法和BP改進算法分組測試實驗結果Table 2 Experimental results comparison between traditional and improved BP algorithm

從表2可以看出：各組中BP改進算法的組內全局均方誤差均明顯小于BP傳統算法的組內全局均方誤差，而對于總體750個測試樣本，BP改進算法的總體全局均方誤差為0.016 81，BP傳統算法的總體全局均方誤差0.558 90，BP改進算法的全局均方誤差只有傳統算法的1/30。該改進算法通過變更傳遞函數傾斜度以及動態調節不同學習速率，很好地克服了傳統BP神經網絡抗干擾能力差、學習速度慢且易陷入局部極小點等缺點，使得傳統BP算法性能進一步提高。

5 結論

（1） 通過分析傳統BP算法的缺點及其成因，改進了網絡訓練方式及傳遞函數，構造了新的復合誤差函數，同時采用了一種分層動態調整不同學習率的新方法，得到一種新的BP改進算法，并采用Lyapunov穩定性方法對該算法的收斂性進行了分析。

（2） 改進算法在收斂速度和避免局部極小方面明顯優于傳統BP算法，很好地克服了傳統BP神經網絡抗干擾能力差、學習速度慢且易陷入局部極小點等缺點，使得BP算法性能進一步提高，是一種訓練BP網絡的有效方法。

[1] 張海東, 賴康生, 代東明, 等. 鋼板無損檢測中基于模糊神經網絡的參數識別[J]. 計算機測量與控制, 2003, 11（1）： 14?17.

ZHANG Hai-dong, LAI Kang-sheng, DAI Dong-ming, et al. Application of fuzzy neural network on parameter recognition of steel strip’s nondestructive testing[J]. Computer Automated Measurement & Control, 2003, 11（1）： 14?17.

[2] 王越, 曹長修. BP網絡局部極小產生的原因分析及避免[J].計算機工程, 2002, 28（6）： 35?37.

WANG Yue, CAO Chang-xiu. Analysis of local minimization for BP algorithm and its avoidance methods[J]. Computer Engineering, 2002, 28（6）： 35?37.

[3] 陳斌, 萬江文, 吳銀鋒, 等. 神經網絡和證據理論融合的管道泄漏診斷方法[J]. 北京郵電大學學報, 2009, 32（1）： 9?13.

CHEN Bin, WAN Jiang-wen, WU Yin-feng, et al. A pipeline leakage diagnosis for fusing neural network and evidence theory[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32（1）： 9?13.

[4] 周輝仁, 鄭丕諤, 牛犇, 等. 基于遞階遺傳算法和BP網絡的模式分類方法[J]. 系統仿真學報, 2009, 29（8）： 2243?2247.

ZHOU Hui-ren, ZHENG Pi-e, NIU Ben, et al. HGA-BP-based pattern classification method[J]. Journal of System Simulation, 2009, 29（8）： 2243?2247.

[5] Kamarthi S V, Pittner S. Accelerating neural network training using weight extrapolations[J]. Neural Networks, 1999, 12（9）： 1285?1299.

[6] Martin F, Moller S. A scaled conjugate gradient algorithm for fast supervised learning[J]. Neural Networks, 1993, 6（3）： 525?533.

[7] Yu C C, Liu B D. A backpropagation algorithm with adaptive learning rate and momentum coefficient[C]//Proceedings of the 2002 International Joint Conference on Neural Networks （IJCNN’02）. Honolulu, 2002： 1218?1223.

[8] WANG Wei, YU Bo. Text categorization based on combination of modified back propagation neural network and latent semantic analysis[J]. Neural Computing and Applications, 2009, 18（8）： 875?881.

[9] WU Wei, SHAO Hong-mei, QU Di. Strong convergence for gradient methods for BP networks training[C]//ZHAO Ming-sheng, SHI Zhong-zhi. Proceedings of 2005 International Conference on Neural Networks and Brains. Beijing： IEEE Press, 2005： 332?334.

[10] MAN Zhi-hong, WU Hong-ren, LIU S, et al. A new adaptive backpropagation algorithm based on Lyapunov stability theory for neural networks[J]. IEEE Trans on Neural Networks, 2006, 17（6）： 1580?1591.

[11] Wong W K, Yuan C W M, Fan D D. Stitching defect detection and classification using wavelet transform and BP neural network[J]. Expert Systems with Applications, 2009, 36： 3845?3856.

[12] 劉勍, 許錄平, 馬義德, 等. 基于脈沖耦合神經網絡的圖像NMI特征提取及檢索方法[J]. 自動化學報, 2010, 7（4）： 931?938.

LIU Qing, XU Lu-ping, MA Yi-de, et al. Image NMI feature extraction and retrieval method based on pulse coupled neural networks[J]. Acta Automatica Sinica, 2010, 7（4）： 931?938.

（編輯 楊幼平）

Improved BP neural network model and its stability analysis

ZHANG Guo-yi, HU Zheng
（Key Laboratory of Universal Wireless Communications of Ministry of Education, Beijing University of Posts and Telecommunications, Beijing 100876, China）

As for shortcomings of classical BP algorithm such as bad anti-jamming ability, low learning rate and easy plunging into local minimum, a new kind of improved BP algorithm was proposed with varying slope of activation function and dynamically adjusting different learning rates. Moreover, the convergence of this improved algorithm was analyzed based on the principle of Lyapunov stability. Considering the deficiency of network training and insufficient learning rate, a new composite error function was invented. A new method of dynamic adjustment of different learning rate was adopted to accelerate the convergence of classical BP algorithm, and to avoid plunging into the local minimum point. The proposed algorithm was applied to the inspection of the surface defective image of steel strips and compared with traditional algorithm with defect detection performance parameters. The results show that the improved BP algorithm has many merits such as high inspection speed, high discrimination and real-time capacity which can satisfy the demand of defect detection on steel plate surface, so it is an effective method.

BP neural network; defect detection; composite error function; Lyapunov stability

TP183

A

1672?7207（2011）01?0115?10

2010?02?06；

2010?07?10

國家科技重大專項（2009ZX03004-001）

張國翊（1982?），男，湖南長沙人，博士研究生，從事無線泛在網絡、認知無線網絡、移動互聯網服務與應用和模式識別研究；電話：13426083917；E-mail： zgysam@gmail.com