一種改進的巖石黏彈塑性加速蠕變力學模型

曹平，劉業科，蒲成志，陳銳，汪亦顯

(中南大學 資源與安全工程學院，湖南 長沙，410083)

一種改進的巖石黏彈塑性加速蠕變力學模型

曹平，劉業科，蒲成志，陳銳，汪亦顯

(中南大學 資源與安全工程學院，湖南 長沙，410083)

為了全面描述巖石蠕變全過程，克服線性牛頓體不能準確描述加速蠕變的不足，在引入非線性蠕變體模型基礎上，結合流變力學模型理論，定義應力與試件長期強度的比值為加速蠕變速率冪級數n，模型發生加速蠕變時的總蠕變量為蠕變特征長度εc，進而得到一種改進的能夠描述巖石黏彈塑性加速蠕變的力學模型。結合東鄉銅礦砂質頁巖單軸壓縮下分級增量循環加卸載蠕變試驗，對模型參數的辨識進行解釋，并將該模型的蠕變擬合曲線與實驗的蠕變曲線進行對比。研究結果表明：該模型能很好地描述了巖石的加速蠕變特性。

流變模型；加速蠕變；蠕變體模型；黏彈塑性模型；長期強度；特征長度

巖石的流變力學特性作為巖石重要的力學特性之一，與巖體結構的長期穩定性緊密相關；許多工程實踐和理論研究都表明巖體的失穩破壞與時間有密切的關系[1]。巖石流變模型研究是巖石流變力學理論中極為重要的部分，限于當前試驗條件的不足，人們對巖石流變學理論的研究并不深入，尤其是對于巖石非線性流變特性的研究成果較少。研究者大多致力于穩態蠕變和定常蠕變的研究，并提出了多種比較成熟的力學模型，如伯格斯模型、西原正夫模型等，但是，這些模型只能較好地描述巖土體的穩態蠕變和定常蠕變，而無法準確描述巖石的加速蠕變。隨著損傷力學的發展，對巖石的時間效應研究進入了非線性損傷研究階段。在巖石脆性損傷及巖體損傷研究的基礎上，金豐年等[2]提出了巖石的非線性流變損傷理論，在此基礎上，鄧榮貴等[3]提出采用非線性牛頓體模型來取代穩定蠕變過程中的線性牛頓體模型，得到了能夠描述巖石加速蠕變狀態的理論模型；趙明華等[4?7]在非線性牛頓體的基礎上進行了大量的研究工作。在實驗研究領域，曹樹剛等[8]發現：受力以后，巖石最初發生裂隙閉合及彈性變形，隨著應力的增加,又產生新的裂隙，并且裂隙越來越多，不斷擴展，導致巖體最終被破壞，為此，基于金豐年等[2]的非線性流變損傷理論，提出巖石黏滯系數先增大、后減小的非線性蠕變模型，并進行了定量描述；此后，何峰等[9?10]在此基礎上進行了進一步分析研究工作。陳沅江等[11]則從另一個角度對軟巖流變模型進行分析研究，提出了適用于軟巖的裂隙塑性體模型和用于描述巖石加速蠕變的蠕變體模型，并對裂隙塑性體和蠕變體的本構關系進行了定量描述。夏才初等[12?13]則提出了同時包含黏彈性、黏塑性、黏性、黏彈塑性4種基本流變力學性態的流變模型，并對模型中各基本元件的參數識別進行了研究。這些研究者對于巖石流變過程中的加速蠕變現象給出了定量的描述和解釋，并在試驗中得到了驗證，取得了階段性成果。巖石在長期荷載作用下發生蠕變現象，其蠕變規律與所施加的應力有直接關系。當應力不大時，巖石試件發生可完全恢復的彈性變形和很小的不可恢復的塑性變形；當應力增大到不大于巖石的長期強度時，將會出現巖石的穩定蠕變階段，其蠕變速率隨加載時間的延長而逐漸趨近于 0；當應力大于巖石的長期強度時，穩定蠕變持續一定時間后，就會轉入加速蠕變，穩定蠕變持續時間和加速蠕變的速率與應力有關。鑒于以上分析，本文作者在陳沅江等[11]提出的蠕變體模型的研究基礎上，進行進一步分析研究工作，提出可用于描述巖石加速蠕變的改進的流變力學模型。

1 蠕變實驗結果

本文實驗結果來源于鐘時猷等[14]對江西東鄉銅礦砂質頁巖進行的分級增量循環加卸載流變實驗。根據文獻[14]，得到砂質頁巖單軸壓縮蠕變實驗的幾個特征參數，見表 1。表 1中：σ為單軸壓縮強度；σb為單軸極限抗壓強度(59.3 MPa)；k為定常蠕變速率；t2為加速蠕變開始時間；t3為蠕變破壞時間；ε2為定常蠕變過程產生的應變；ε3為加速蠕變過程產生的應變；ε為破壞時的總應變。

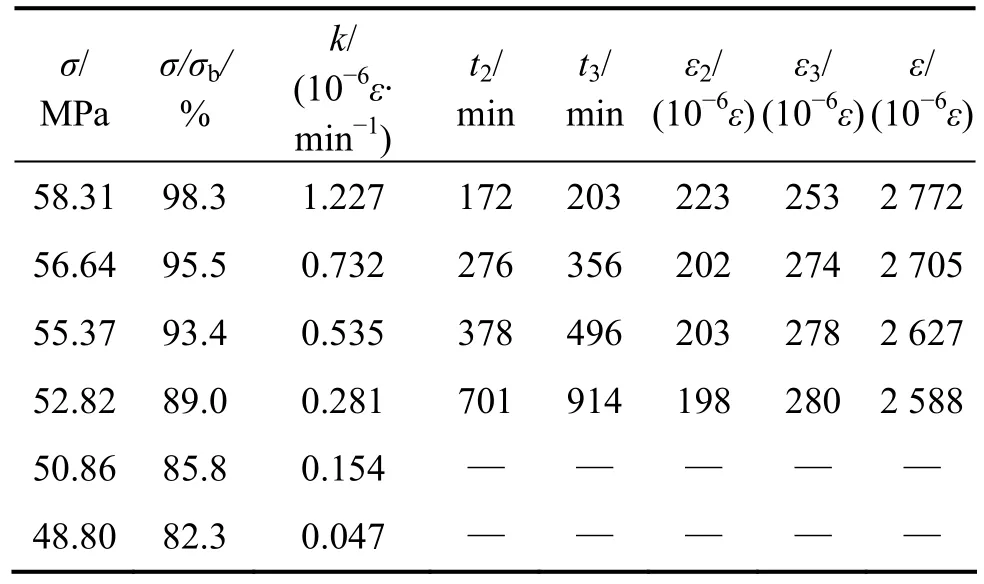
表1 砂質頁巖單軸壓縮蠕變試驗特征參數Table 1 Characteristic parameters of uniaxial compression creep tests of sandy shale

2 流變力學模型

2.1 改進的CYJ體

改進的 CYJ體(見圖 1)是在 CYJ體(即由陳沅江等[11]提出的描述巖體加速蠕變狀態的非線性牛頓體?蠕變體元件)基礎上，保留其引入的 3個模型參數(加速蠕變冪級數n、黏滯系數ηc和模型初始長度εc)，但是，這是對εc與n進行了更準確的物理定義后得到的。改進的CYJ體中，蠕變體具有與CYJ體中蠕變體相同的蠕變特性：當蠕變體變形在εc內，蠕變體元件表現出與線性牛頓體相同的蠕變特性；當蠕變體變形大于εc時，蠕變體元件表現出非線性牛頓體的蠕變特性。其本構關系為：

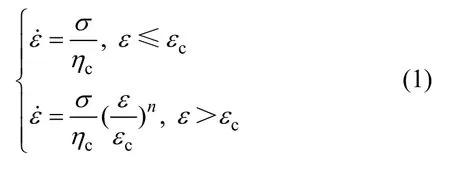
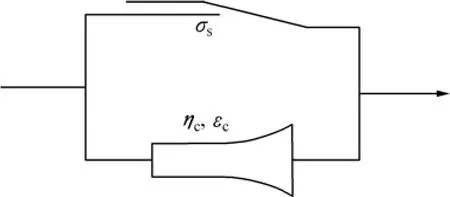
圖1 非線性牛頓體(改進的CYJ體)Fig.1 Nonlinear Newton fluid (improved CYJ body)

式中：ε為模型總的蠕變變形量，為模型蠕變速率；ηc為蠕變體元件的黏滯系數；n為巖石流變實驗的應力σ與長期強度σ∞的比值，即σn=σ/∞；∞根據流變實驗確定，在無實驗數據條件下，可以根據文獻[14]確定；εc為流變模型的初始長度，為n的二次函數，即εc=A+Bn+Cn2；A，B和C各參數根據流變實驗確定。

對式(1)關于時間求解微分方程，得：

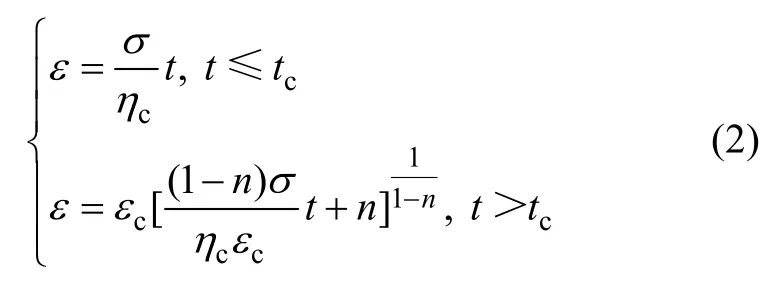
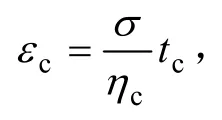
2.2 巖石黏彈塑性流變力學模型的確定及其力學特性

2.2.1 流變模型組合元件的確定

巖石在恒定應力作用下，最初發生彈性變形及原生裂隙的閉合現象，隨著時間的逐漸增加，巖石內部原生裂隙損傷也逐漸積累，并向巖體內部擴展，在巖石內部缺陷處產生新的裂紋，并且裂紋演化越來越多，同時進一步擴展，直至巖石最終破壞。當恒定應力較小，不足以引起巖石內部原生裂隙擴展時，就不會導致巖石最終破壞。

巖石的蠕變曲線如圖2所示，其中：σi(i=1, 2, 3)為巖石流變實驗所施加的應力，且σ3＞σ2＞σ1。根據應力條件的不同，巖石呈現出瞬時蠕變、穩定蠕變和加速蠕變3個蠕變變形階段，相應地，理想的復合流變模型應該能夠很好地表現出上述 3個蠕變變形階段。根據經驗，上述蠕變形態可以用下面的數學公式給出：

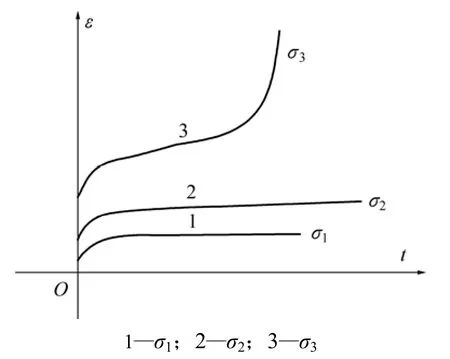
圖2 巖石典型蠕變曲線Fig.2 Typical creep curves of rock

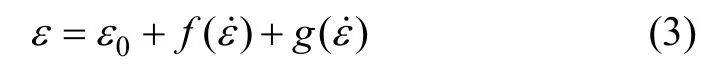
式中：ε0為瞬時蠕變；f()為衰減蠕變和定常蠕變組成的穩態蠕變；為時間的減函數；g()為加速蠕變，為時間的增函數。

根據式(3)，Hook體可以模擬理想的線彈性變形，Kelvin體可以模擬穩定蠕變，但是，它們不能模擬瞬時彈性變形；因此，選擇將Hook體與Kelvin體串聯組成H-K模型，用以模擬巖石瞬時蠕變和穩態蠕變過程。但是，巖石在完全卸載時，會有不可恢復的殘余變形存在，而Hook-Kelvin模型不能模擬完全卸載后的殘余變形存在，因此，在Kelvin體上并聯1個圣維南體，使流變模型具有描述不可恢復的殘余變形的特性，然后，與本文提出的改進的CYJ體串聯，組成適用于巖石黏彈塑性流變力學模型，如圖3所示。

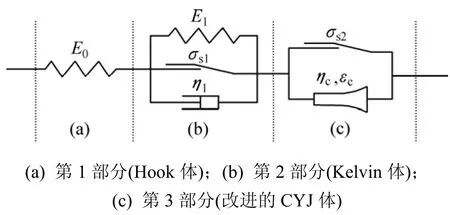
圖3 巖石黏彈塑性流變力學模型Fig.3 Rheological mechanical model with viscoelastic plasticity of rock

2.2.2 流變模型特性

從圖3可知：模型是Hook體、圣維南體、Kelvin體和改進的 CYJ體的組合體，當模型只有(a)和(b)作用且σs1=0時，模型退化為三參量模型；當模型中(a)，(b)和(c)均參與作用，且ε≤εc和σs1=0時，模型退化為西原正夫模型。

(1) 當σ＜σs1＜σs2時，模型中只有(a)起作用，相應的蠕變方程為：

(2) 當σs1＜σ＜σs2時，模型中(a)和(b)起作用，根據模型組合特性，相應的蠕變方程為：

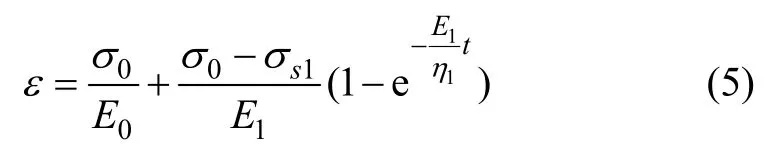
(3) 當σs1＜σs2＜σ時，模型中的(a)，(b)和(c)均起作用，根據改進的CYJ體的蠕變特性，此應力條件下的巖石蠕變分為以下2部分。

① 當ε≤εc時，改進的CYJ體(c)表現出與線性牛頓體相似的特性，根據式(2)和式(3)，得到模型的蠕變方程：

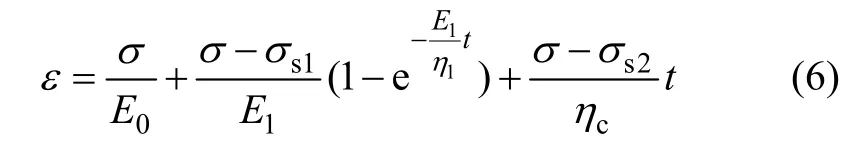
② 當ε＞εc時，改進的CYJ體(c)表現出非線性蠕變特性，根據式(2)與式(3)，得到模型的蠕變方程：

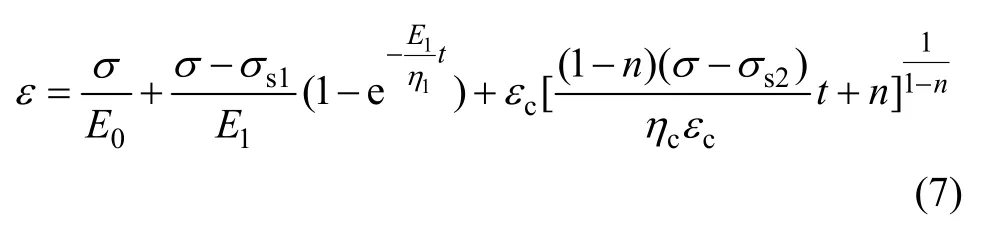
式中：σ0，σ1和σ2分別為圖 3 中模型(a)，(b)和(c)的應力；ε0，ε1和ε2分別為模型(a)，(b)和(c)的應變；E0和E1分別為模型(a)和(b)的彈性模量；η1和ηc分別為模型(b)和(c)的粘滯系數；εc為系統應變初始長度；σs1和σs2分別為模型(b)和(c)的材料塑性體發生塑性變形的應力門檻值。

3 流變力學模型參數

由圖3可知：該模型共有7個參數，其中包括2個彈性參數E0和E1(E0表征模型的瞬時彈性特征，E1表征模型的固化彈性特征)、2個黏性系數η1和ηc(η1表征模型的固化黏性特征，ηc表征模型的流動黏性特征)、2個屈服極限σs1和σs2(σs1表征模型固化變形過程中的摩擦阻力，σs2表征模型的長期強度)、1個特征長度εc(表征模型加速蠕變時的蠕變變形總量)。下面對其變化規律進行進一步解釋。

馬明軍等[15]對于除ηc與εc2個表征加速蠕變的參量外，都給予了明確的解釋，這里引用其研究成果，并對ηc與εc這2個參數的確定給予進一步解釋，E0=3×104MPa。

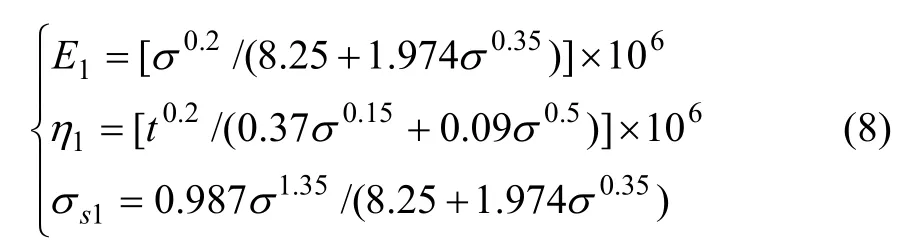
當荷載大于長期強度時，改進的CYJ體才會參與作用，并產生黏塑性流動變形，根據文獻[13]，得到東鄉銅礦砂質頁巖長期強度：

此時，流動變形速率為：

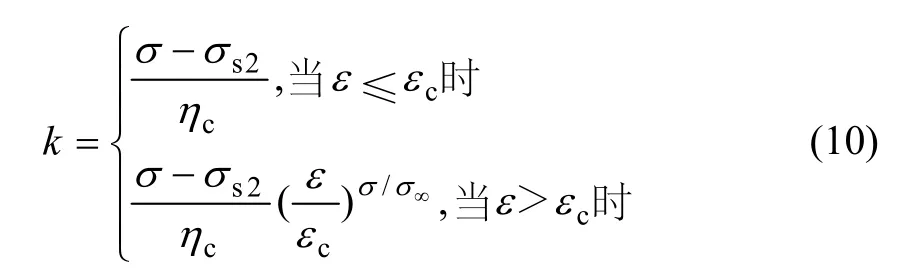
根據實驗結果(表1)回歸得到：

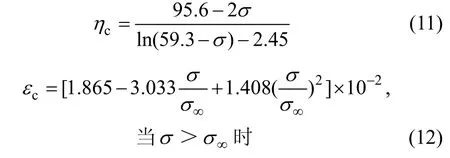
根據參數識別結果，對模型曲線在不同應力下進行擬合，并與實驗曲線對比。這里給出6個不同應力下的流變實驗曲線和力學模型的擬合曲線，如圖 4所示。

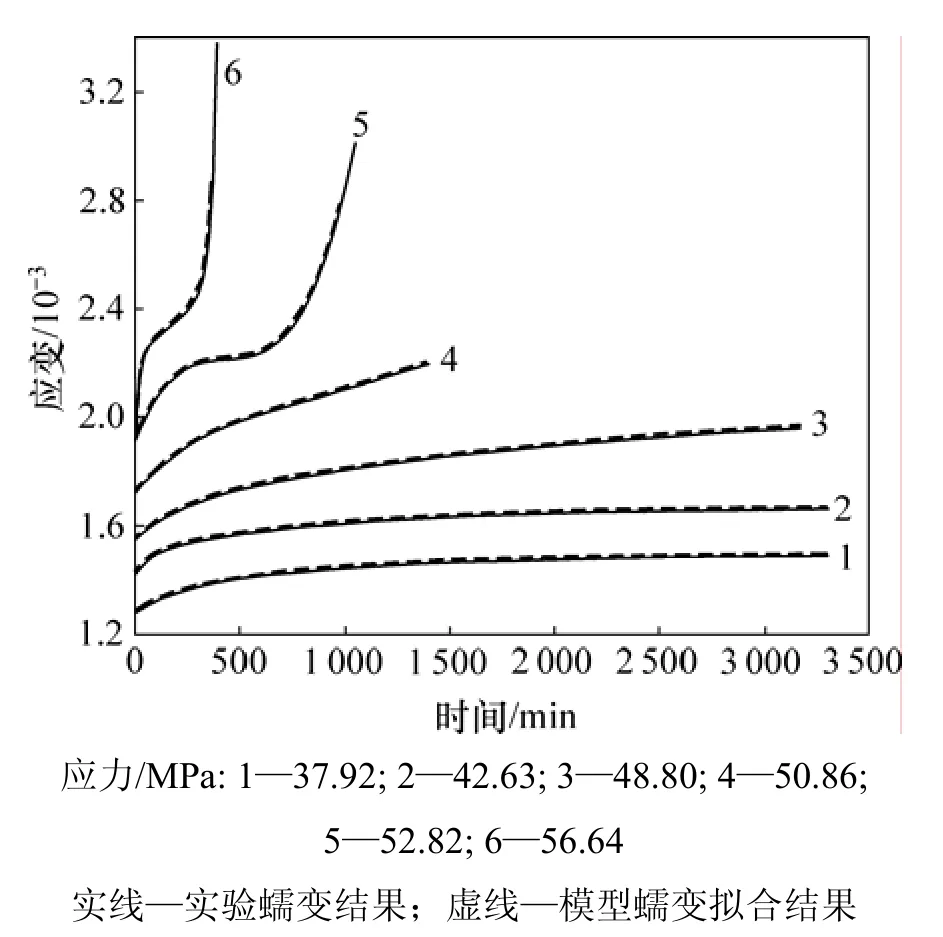
圖4 非線性流變模型蠕變擬合曲線與實驗結果比較Fig.4 Comparisons between fitting curves of nonlinear rheological model and experimental curves

從圖4可以看出：本文提出的巖石黏彈塑性流變力學模型對巖石加速蠕變過程的擬合效果較好，證明了本文建立的力學模型的正確性和合理性。

4 結論

(1) 在引進非線性蠕變體模型的基礎上，通過對巖石流變實驗過程中加速蠕變階段實驗數據進行分析，提出特征長度εc與加速蠕變冪級數n更加明確的物理意義，使模型表達更加簡潔、明確；建立了一種能夠反映巖石黏彈塑性加速蠕變的改進的復合力學模型，根據東鄉銅礦砂質頁巖單軸壓縮下分級增量加卸載蠕變試驗結果，對模型參數的辨識進行簡要解釋。

(2) 對新建立的黏彈塑性流變力學模型的蠕變曲線進行擬合，并與試驗蠕變曲線進行對比，發現擬合曲線與試驗曲線較吻合，證明所建模型能夠很好地反映巖石蠕變全過程的力學響應。

(3) 巖石力學參數不是常數，而是與應力和時間有關的變量，這進一步揭示了巖石流變力學性質的特點。

(4) 為了得到更精確的力學模型參量，對于力學模型參數確定方法有待進一步研究。

[1] 蔣昱州, 張明鳴, 李良權. 巖石非線性黏彈塑性蠕變模型研究及其參數識別[J]. 巖石力學與工程學報, 2008, 27(4):832?839.

JIANG Yu-zhou, ZHANG Ming-ming, LI Liang-quan. Study on nonlinear viscoelasto-plastic creep model of rock and its parameter identification[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 832?839.

[2] 金豐年, 范華林. 巖石的非線性流變損傷模型及其應用研究[J]. 解放軍理工大學學報, 2000, 1(3): 1?5.

JIN Feng-nian, FAN Hua-lin. Study of nonlinear rheology damage property of rock[J]. Journal of PLA University of Science and Technology, 2000, 1(3): 1?5.

[3] 鄧榮貴, 周德培, 張倬元, 等. 一種新的巖石流變模型[J]. 巖石力學與工程學報, 2001, 20(6): 780?784.

DENG Rong-gui, ZHOU De-pei, ZHANG Zhuo-yuan, et al. A new rheological model for rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 780?784.

[4] 趙明華, 肖燕, 陳昌富. 軟土流變特性的室內試驗與改進的西原模型[J]. 湖南大學學報: 自然科學版, 2004, 31(1): 48?51.

ZHAO Ming-hua, XIAO Yan, CHEN Chang-fu. Laboratory experiment of the rheological property of soft clay and the improved Xiyuan model[J]. Journal of Hunan University:Natural Sciences, 2004, 31(1): 48?51.

[5] 鄒友平, 鄒友峰, 郭文兵. 改進的西原模型及其穩定性分析[J]. 河南理工大學學報, 2005, 24(1): 22?24.

ZOU You-ping, ZOU You-feng, GUO Wen-bing. The modified Xiyuan model and its stability analysis[J]. Journal of Henan Polytechnic University, 2005, 24(1): 22?24.

[6] 王小平. 對改進西原模型的再認識[J]. 河海大學學報: 自然科學版, 2007, 35(6): 651?654.

WANG Xiao-ping. Reevaluation of modified Xiyuan model[J].Journal of Hohai University: Natural Sciences, 2007, 35(6):651?654.

[7] 蔣昱州, 徐衛亞, 王瑞紅, 等. 巖石非線性蠕變損傷模型研究[J]. 中國礦業大學學報, 2009, 38(3): 331?335.

JIANG Yu-zhou, XU Wei-ya, WANG Rui-hong, et al. Nonlinear creep damage constitutive model of rock[J]. Journal of China University of Mining & Technology, 2009, 38(3): 331?335.

[8] 曹樹剛, 邊金, 李鵬. 巖石蠕變本構關系及改進的西原正夫模型[J]. 巖石力學與工程學報, 2002, 21(5): 632?634.

CAO Shu-gang, BIAN Jin, LI Peng. Rheologic constitutive relationship of rocks and a modifical model[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(5): 632?634.

[9] 何峰, 王來貴，于永江, 等. 巖石試件非線性蠕變模型及其參數確定[J]. 遼寧工程技術大學學報, 2005, 24(2): 181?183.

HE Feng, WANG Lai-gui, YU Yong-jiang, et al. Non-linear creep model of rock and parameter determination[J]. Journal of Liaoning Technical University, 200, 24(2): 181?183.

[10] 王來貴, 何峰, 劉向峰, 等. 巖石試件非線性蠕變模型及其穩定性分析[J]. 巖石力學與工程學報, 2004, 23(10): 1640?1642.

WANG Lai-gui, HE Feng, LIU Xiang-feng, et al. Non-linear creep model and stability analysis of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(10): 1640?1642.

[11] 陳沅江, 潘長良, 曹平, 等. 軟巖流變的一種新力學模型[J].巖土力學, 2003, 24(2): 209?214.

CHEN Yuan-jiang, PAN Chang-liang, CAO Ping, et al. A new mechanical model for soft rock rheology[J]. Rock and Soil Mechanics, 2003, 24(2): 209?214.

[12] 夏才初. 統一流變力學模型的若干問題研究[C]//第六次全國巖石力學與工程學術大會論文集. 武漢, 2000: 199?202.

XIA Cai-chu. A study on some problem of unitized rheology model[C]//Proceedings of the 6th Rock Mechanics and Engineering Conference. Wuhan, 2000: 199?202.

[13] 夏才初, 許崇幫, 王曉東, 等. 統一流變力學模型參數的確定方法[J]. 巖石力學與工程學報, 2009, 28(2): 425?532.

XIA Cai-chu, XU Chong-bang, WANG Xiao-dong, et al.Method for parameters determination with unified rheological mechanical model[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2): 425?532.

[14] 鐘時猷, 馬明軍. 軟弱巖石蠕變破壞規律的探討[J]. 中南礦冶學院學報, 1987, 18(5): 494?500.

ZHONG Shi-you, MA Ming-jun. An approach to creep failure regularity of weak rock[J]. J Cent South Inst Min Metall, 1987,18(5): 494?500.

[15] 馬明軍，鐘時猷. 一個軟弱巖石的粘彈塑性流變力學模型[J].中南礦冶學院學報, 1990, 20(3): 236?241.

MA Ming-jun, ZHONG Shi-you. A new visco-elastic plastic rheological mechanical model for soft rocks[J]. J Cent South Inst Min Metall, 1990, 20(3): 236?241.

(編輯 陳燦華)

An improved accelerated creep mechanical model of viscoelasto-plastic rock

CAO Ping, LIU Ye-ke, PU Cheng-zhi, CHEN Rui, WANG Yi-xian

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

In order to depict the process of rock creep comprehensively, and overcome the deficiency of the linear Newton fluid which can not describe accelerated creep accurately, based on the mature rheological model, the nonlinear creep body model was introduced. In this model, the total creep strain before accelerated creep stage was defined as the characteristic length of creep, and the ratio of stress level and long-term strength of rock specimens was defined as accelerated creep rate. The improved rheological mechanics model was established that can describe the viscoelastic-plastic characteristics of accelerated creep. Combined with the uniaxial compression creep test under multi-step incremental cycling loading and unloading on the sandy shale from Dongxiang Copper Mine, the parameter identification of the mechanical model was explained, the experimental creep curve was compared with the creep fitted curve obtained by the model. The results show that the accelerate creep properties of rocks can be described effectively by this improved creep model.

rheological model; accelerated creep; creep body model; viscoelasto-plastic model; long-term strength;characteristic length

TU452

A

1672?7207(2011)01?0142?05

2010?03?29；

2010?06?03

國家自然科學基金資助項目(10972238)；教育部博士點基金資助項目(20090162110037)；中南大學研究生學位論文創新選題基金資助項目(134377237)

劉業科(1981?)，男，廣西融安人，博士研究生，從事巖土工程學的理論、實驗及穩定性研究；電話：13549673869；E-mail: 20732701@qq.com