基于單元模態應變能靈敏度的結構損傷統計識別

顏王吉，黃天立，任偉新

(中南大學 土木建筑學院，湖南 長沙，410075)

基于單元模態應變能靈敏度的結構損傷統計識別

顏王吉，黃天立，任偉新

(中南大學 土木建筑學院，湖南 長沙，410075)

基于單元模態應變能靈敏度, 采用概率統計的方法，提出一種同時考慮模型不確定性和測試噪聲影響的損傷統計識別方法。首先，建立基于單元模態應變能靈敏度分析的結構損傷方程組，然后，通過攝動法推導出損傷結構剛度參數的統計特性，并運用損傷概率模型計算各單元的損傷存在概率。最后，用一簡支梁數值模擬算例驗證了該方法的有效性。研究結果表明：損傷概率越大，表明存在損傷的可能性越大；損傷單元的損傷存在概率大于非損傷單元的損傷存在概率；隨著損傷程度的增加，損傷存在概率不斷增加，而隨著噪聲水平的增加，損傷存在概率減小。

靈敏度；模態應變能；模態分析；損傷識別；統計方法

基于動力特性的結構損傷識別分析方法的核心問題之一是尋找對結構損傷敏感的損傷參數，由動力參數的變化判斷結構損傷情況[1?2]。近年來，模態應變能在機械工程、航天工程和土木工程等領域引起了廣泛關注。Lim 等[3?10]等國內外學者都將模態應變能用于結構損傷識別，取得了較滿意的結果。目前，基于模態應變能的損傷識別方法以確定性分析方法為主，即根據參數識別結果和相應設計基準值直接對比判別損傷的位置和程度。在工程實際中，測試數據不可避免地要受到噪聲、環境因素及運營條件的影響，建模所用的信息也具有不確定性，損傷識別需要考慮這些不確定性因素。尤其是土木工程作為“建造”系統，區別于機械等“制造”系統，不確定因素更多；因此，以確定性方法處理具有本質不確定性的土木工程結構損傷識別問題，導致理論方法與實際應用的矛盾，造成損傷識別結果可靠性差[11]。概率統計理論作為處理不確定性問題的有效工具，將其引入損傷識別可以有效提高識別結果的穩定性和可靠性[12]。相對于確定性損傷識別方法，基于概率統計理論的損傷識別方法能夠更好地反映損傷識別問題的不確定性本質。通過將不確定性轉化為概率統計意義上的數學表述，從而有效克服其缺陷，是一種比較行之有效的損傷識別方法。本文作者采用概率統計的方法，基于單元模態應變能靈敏度，提出一種同時考慮模型不確定性和測試噪聲影響的損傷統計識別方法。首先，建立基于單元模態應變能靈敏度分析的結構損傷方程組；然后，采用攝動法推導出損傷結構剛度參數的統計特性，并運用損傷概率模型計算各單元的損傷存在概率，損傷概率越大，表明存在損傷的可能性越大；最后，用1個簡支梁數值模擬算例驗證本文方法的有效性，并考慮噪聲水平和損傷程度對識別結果的影響。

1 基于單元模態應變能靈敏度的損傷識別

基于代數算法可以推導出單元j對應的r階模態應變能(Qjr)對任意設計參數(p)的一階靈敏度表達式[13]：

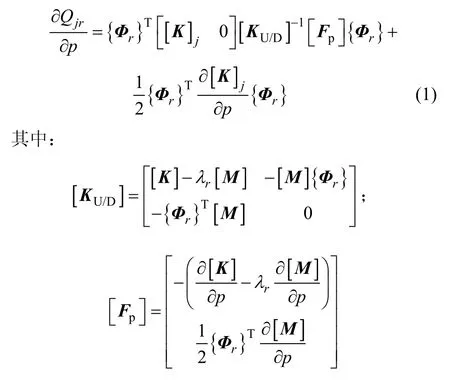
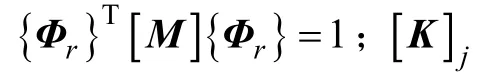
為了將結構的健康狀況描述清楚，需要選取適當的指標，使之既能反映結構的損傷位置，又能反映結構的損傷程度。在有限元層次上，結構單元的損傷可以用各個有限單元的剛度的降低幅度表示(此處用擴階后的單元剛度矩陣表示)：

由單元模態應變能的靈敏度的代數表達式可以推導出基于單元模態應變能變化的結構損傷方程組[10]：

通過求解該損傷方程組，能夠同時識別結構損傷位置和損傷程度，是直接的(不需迭代的)損傷識別方法。然而，求解損傷方程組(3)進行結構損傷識別是一種確定性的方法，沒有考慮土木工程中的不確定性，不符合實際工程的需要, 因此，需要引入概率統計方法，使之既能考慮模型的不確定性，又能考慮測試噪聲的誤差。

2 基于單元模態應變能靈敏度的損傷統計識別

結構整體剛度矩陣和質量矩陣可以表示為：

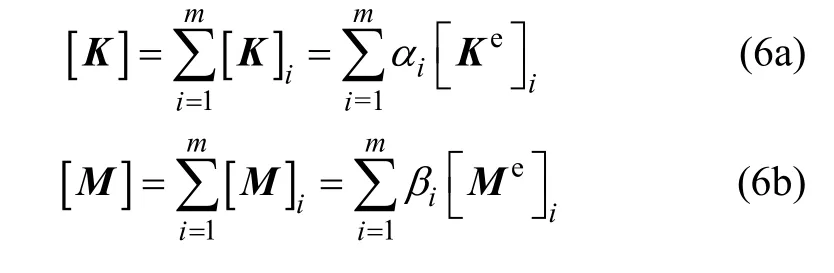
式中：i和i分別代表損傷前“單元剛度參數”( ESP)和“單元質量參數”(EMP)。以 Euler–Bernoulli梁為例，其ESP為抗彎剛度(EI)，EMP為單位梁長的質量。損傷后的“單元剛度參數”和“單元質量參數”分別用和表示。因此，損傷因子可以表示為：

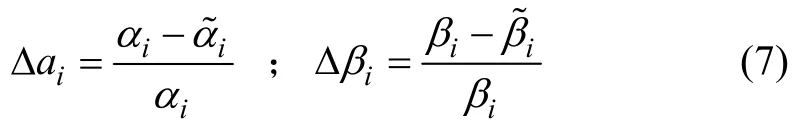
假設測得的模態參數及系統結構設計參數均為隨機變量，它們的誤差(這里只考慮偶然誤差，不考慮系統誤差)服從均值為0的正態分布，且互相獨立[14]；因此，損傷結構的振型值、結構物理參數(單元剛度參數和單元質量參數)如下所示：

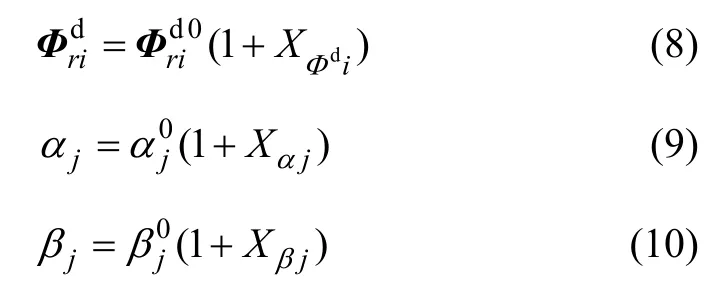
其中：i=1, 2, …,n，n為測試得到的振型矢量元素個數；j=1, 2, …,m(m為結構物理參數數目，此處即單元劃分數目)；“0”代表各物理量的均值；，Xαj和Xβj分別為相應物理量的隨機噪聲。為方便分析，將，Xαj和Xβj合寫為新的噪聲矢量{X}。由假設可知，E(Xk)=0。

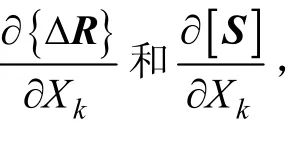
由式(5)，將ΔRjr對噪聲Xk求偏導數得:

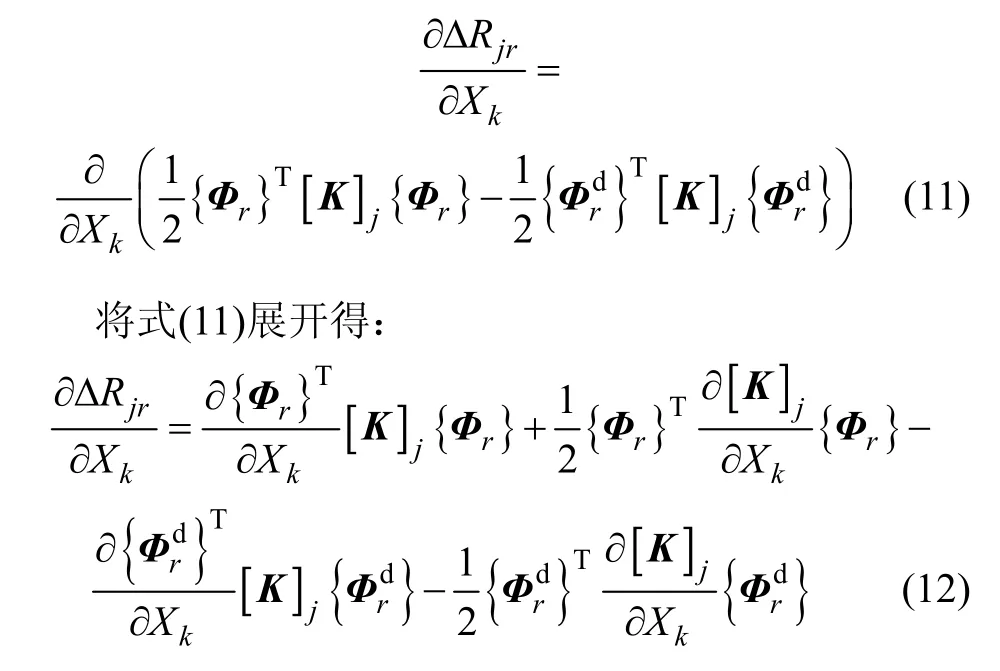
同理，根據式(4)，將Sjir對噪聲Xk求偏導數得：

當i≠j時，

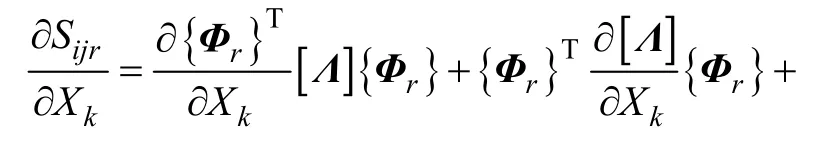
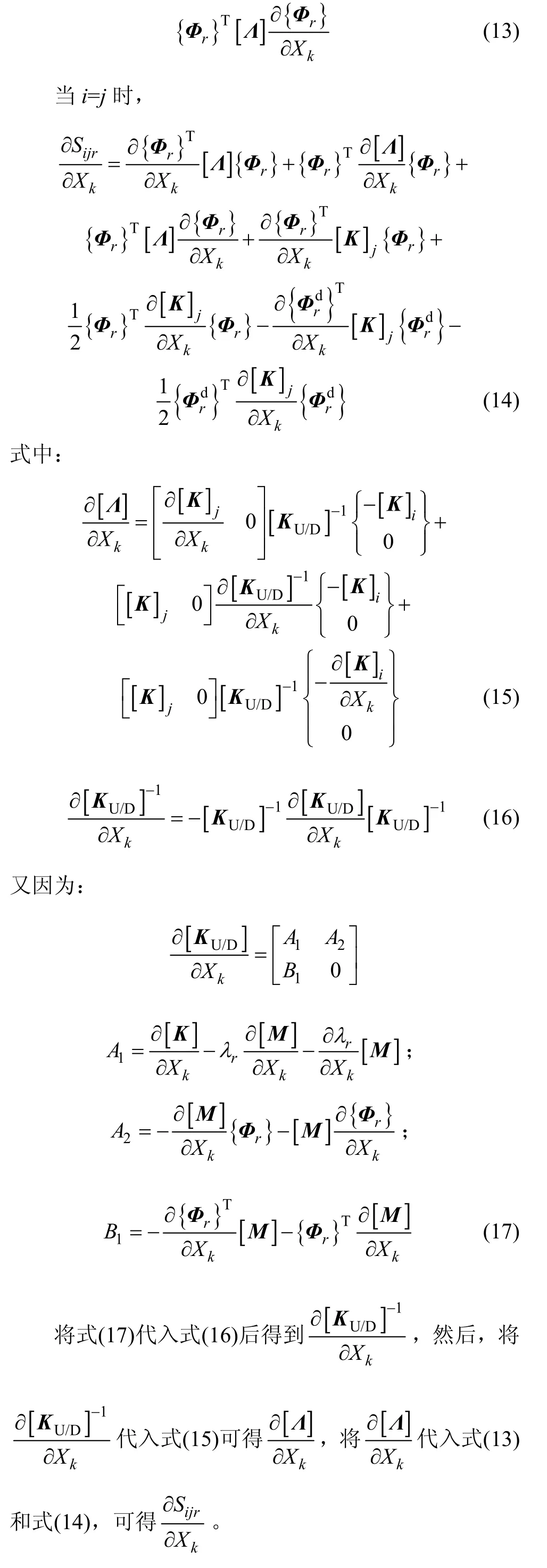
由攝動理論，損傷方程組(3)可以展開為關于噪聲向量X的一階泰勒公式：

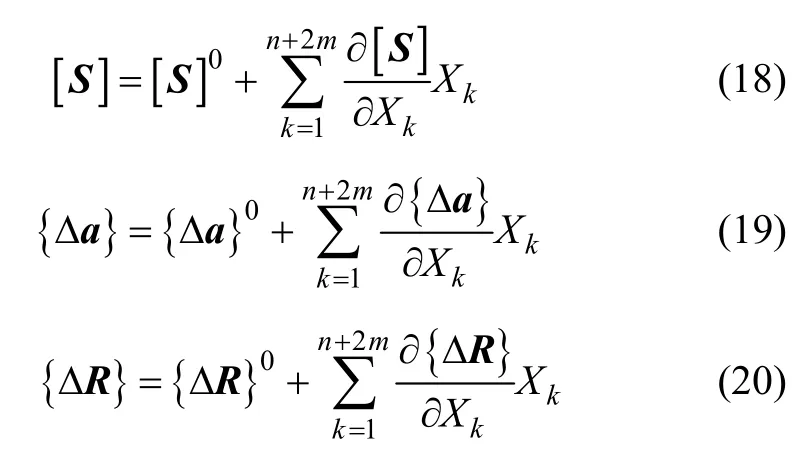
將式(18)～(20)代入損傷方程組(3)，可得：

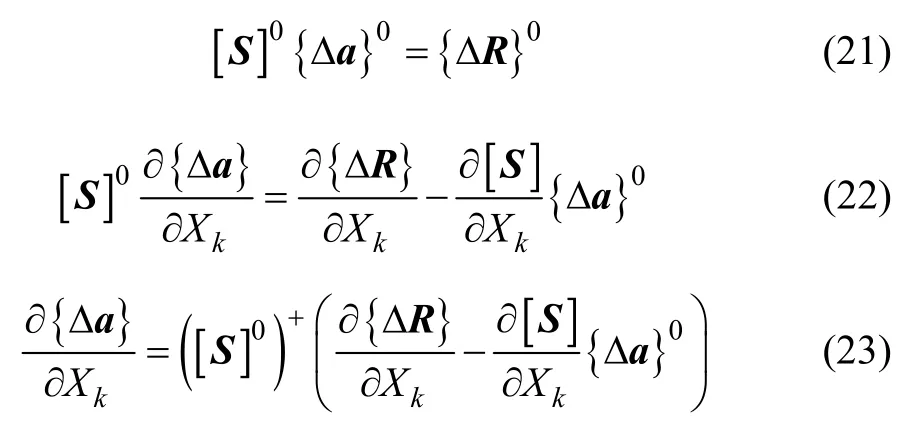
由于E(Xi)=0，根據式(19), 可得損傷指數的均值為：

式中：下標表示矩陣階數。

因此，損傷后單元剛度參數的統計特性為：

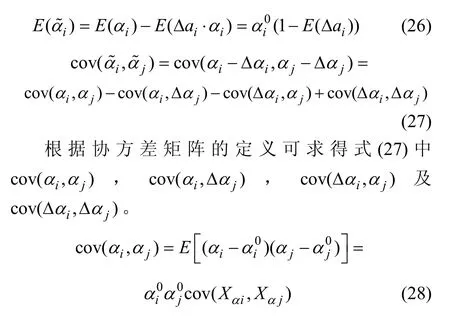
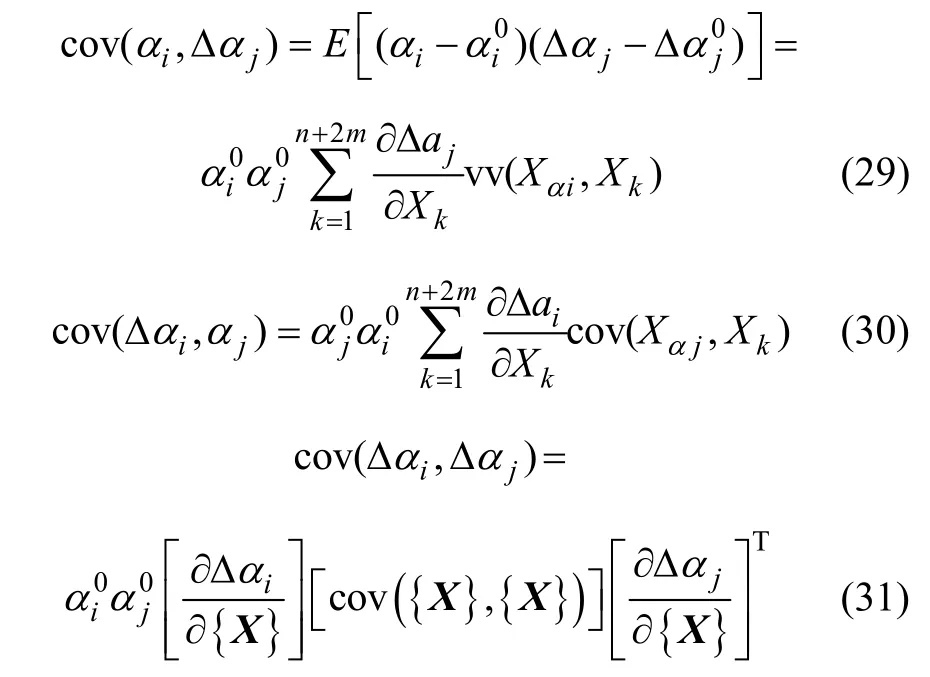
將式(28)～(31)代入式(27)即可得協方差矩陣，這樣，由式(26)和(27)可以計算出結構各單元剛度參數的統計特性。需要特別說明的是：由于系數矩陣的列幾乎是線性相關的，損傷方程為病態，因而，求逆時，需要先引入奇異值截斷算法[15]對系數矩陣進行奇異值截斷，保證系數矩陣的數值穩定。

3 損傷的概率判別方法

從結構損傷前后剛度參數的統計分布的變化可以估計出結構的損傷概率[14]，其基本思路是在給定置信度的條件下，在定義的概率密度損傷區間內，計算結構剛度參數的概率。例如，設未損傷時單元的剛度參數服從正態分布 N(E(),σ2())，其概率密度函記為PDF(Probability density function)。結構無損時的剛度參數區間定義為?(i,)，其含義是結構在給定的區間內，i的概率為 ，即

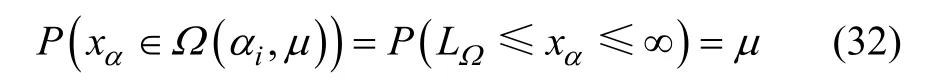
式中：LΩ是給定健康區間的下界； Ω(αi,μ)取決于需要的置信度 ，當 為 95%時，LΩ為E(αi)?1.645σ2(αi)，它意味著無損的結構剛度參數落在 [E(αi)?1.645σ2(αi),∞]中的概率為95%。如果i單元發生損傷，此時其剛度參數服從正態分布N(E() ,σ2())，其單元損傷概率PDE(Probability of damage existence)定義為在 Ω(αi,0.95)以外的概率部分的值，即：

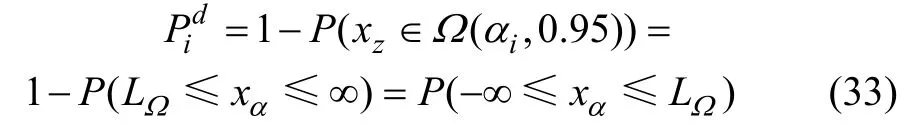
損傷概率取值區間為(μ, 1)，顯然，結構損傷概率越接近1，損傷越可能發生；損傷概率越接近0，損傷越不可能發生。

由以上分析可知基于單元模態應變能靈敏度分析的損傷統計識別方法的基本思路為：假設損傷結構參數不確定性和測試噪聲均服從正態分布，利用攝動法可以求出損傷結構各單元剛度參數的統計特性(均值和方差)。若已知未損結構和損傷結構剛度參數的概率分布，則根據上面的損傷概率判別方法可以確定結構的損傷存在概率(PDE)，從而達到識別結構損傷的目的。單元的損傷存在概率越大，表明該單元是損傷單元的可能性越大。

4 數值算例

采用的數值試驗模型為Euler-Bernoulli梁，如圖2所示。梁總長為6 m，劃分為10個單元。假設未損結構的幾何參數和物理參數(均值)如下：梁的橫截面積A為 0.005 m2，慣性矩I=1.67×10?4m4，彈性模量E=32 GPa，容重ρ=2.5 t/m3。

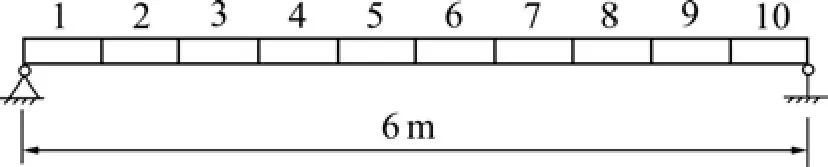
圖1 Euler-Bernoulli梁Fig.1 Simulated Euler-Bernoulli beam

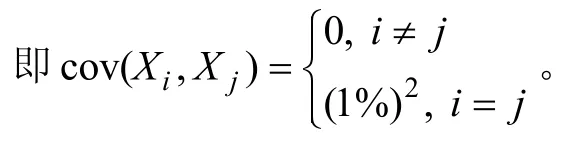
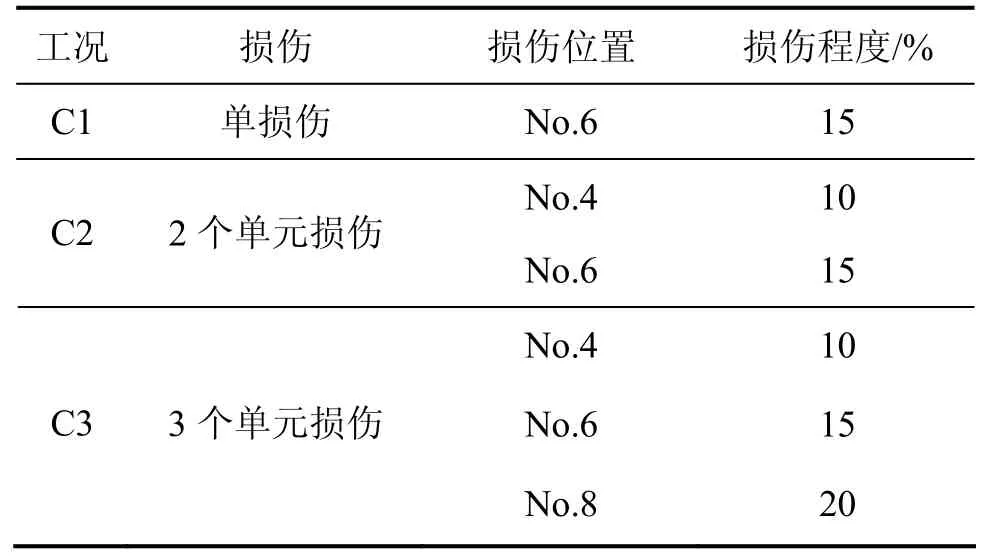
表1 數值試驗梁損傷工況Table 1 Simulated damage scenarios

由上面建立的損傷概率判別方法，可以得到每個單元的損傷存在概率，如圖2所示。計算結果表明：3種損傷工況的損傷單元的損傷存在概率遠大于非損傷單元的損傷存在概率，說明該方法能有效地識別出損傷單元。

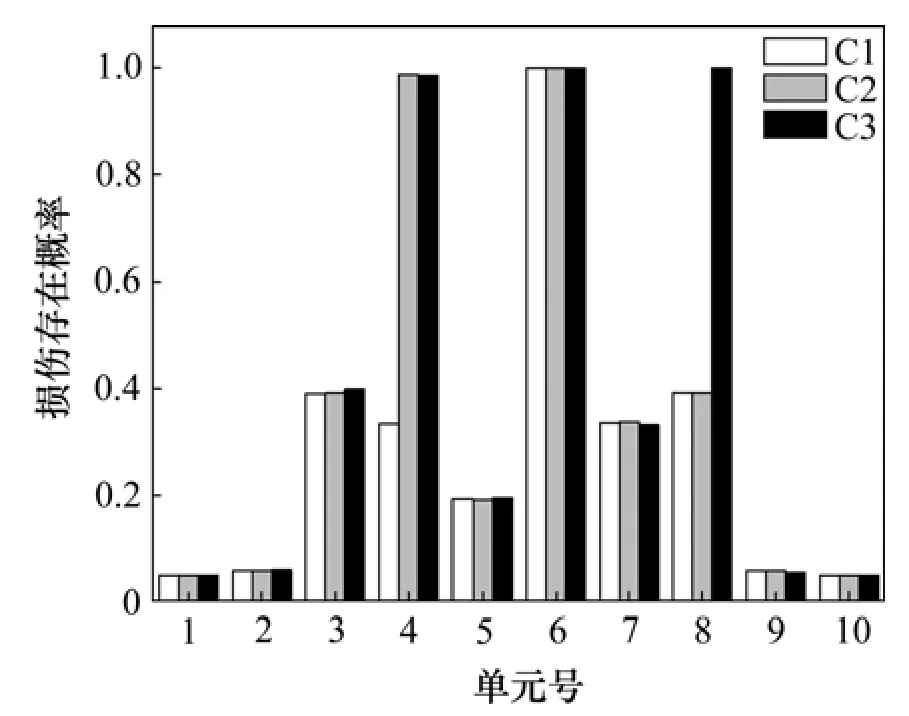
圖2 各單元損傷存在概率Fig.2 Probability of damage of different elements

為研究不同程度的損傷識別效果，在噪聲水平保持不變(1%)前提下，在不同的損傷水平下，前6個單元的損傷存在概率如圖3所示。此外，為研究噪聲水平的影響，假定噪聲水平由1%不斷增加為2%，3%，5%和10%，并假設單元3，4，5和6同時發生損傷，且損傷程度均為15%，前6個單元的損傷存在概率如圖4所示。

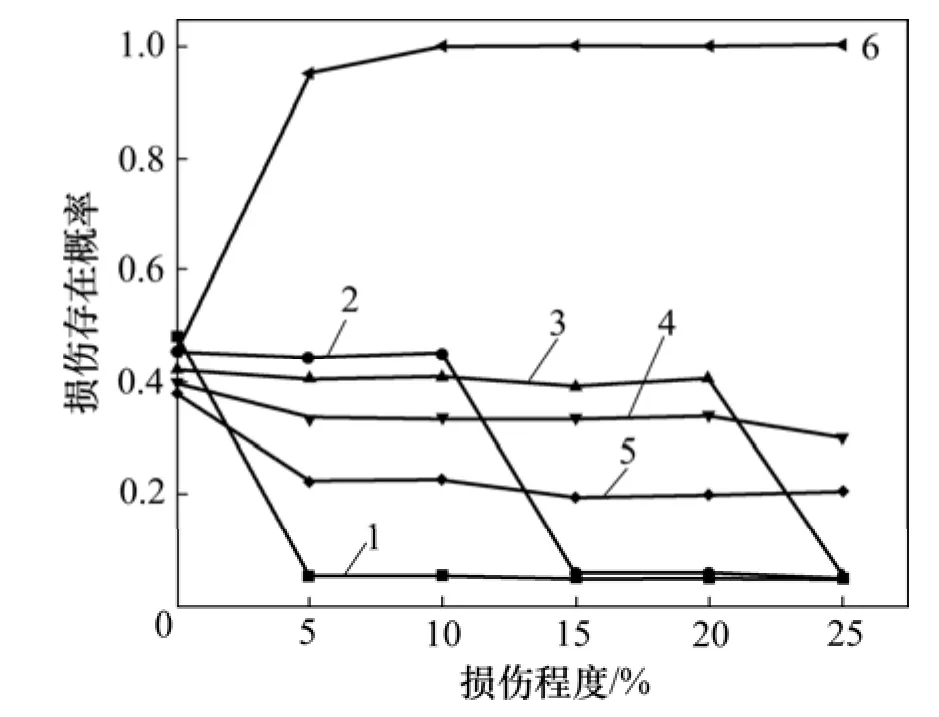
圖3 損傷存在概率隨損傷程度變化規律Fig.3 Change of PDE with increase of damage level

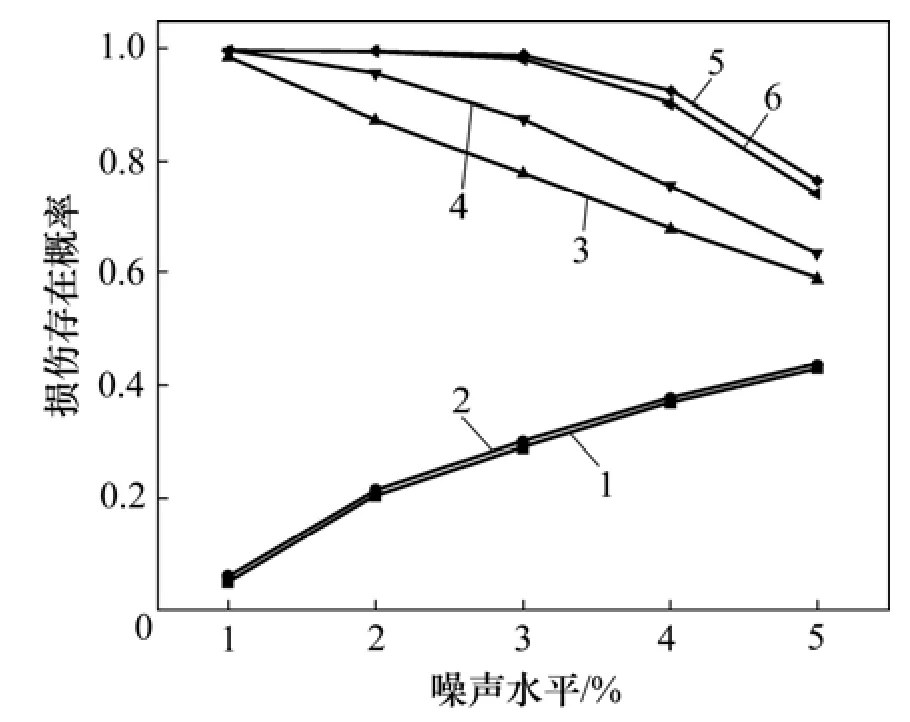
圖4 損傷存在概率隨噪聲水平變化規律Fig.4 Change of PDE with increase of noise level

由圖4可見：隨著損傷程度的增加，損傷存在概率不斷增加，而未損傷單元的存在概率總體上隨著損傷程度的增加而減少；隨著噪聲水平的增加，損傷單元存在概率不斷減小，而未損傷單元存在概率總體上隨著噪聲水平的增加而增加，說明噪聲對損傷識別結果有較大的影響。在5種噪聲水平下，單元5和單元6的損傷存在概率大于單元3和單元4的損傷存在概率，而且隨著噪聲增加，單元3和單元4的損傷存在概率下降速率更快；因此，損傷位置對統計識別結果有影響，靠近支座位置損傷比遠離支座損傷更難識別，損傷識別結果的準確度和置信度與損傷程度、噪聲水平有關。在噪聲水平不太大時，本文方法能識別損傷位置。

5 結論

(1) 建立了基于單元模態應變能靈敏度的結構損傷方程組，通過攝動法推導了損傷結構剛度參數的統計特性，然后，運用損傷概率模型計算各單元的損傷存在概率。表達式簡潔緊湊，充分利用了矩陣運算的優點，便于編程，便于存儲，適用于分析工程領域的大型結構(剛度矩陣和質量矩陣的維數很大)。此外，該方法僅需較少的模態信息，甚至一階模態信息就足夠，沒有模態截斷引起計算誤差的問題。

(2) 損傷單元損傷存在概率遠大于非損傷單元的損傷存在概率, 能有效地識別出損傷單元；損傷識別結果的準確度和置信度與損傷程度、噪聲水平和損傷位置有關；當噪聲水平不是太大時，可以識別損傷位置。隨著損傷程度的增加，損傷存在概率不斷增加，而未損單元的損傷存在概率總體上隨著損傷程度的增加而減少。

[1] Ren W X, De roeck G. Structural damage identification using modal data (Ⅰ): Simulation verification[J]. Journal of Structural Engineering, ASCE, 2002, 128(1): 87?95.

[2] Ren W X, De roeck G. Structural damage identification using modal data (Ⅱ): Test verification[J]. Journal of Structural Engineering, ASCE, 2002, 128(1): 96?104.

[3] Lim T W, Kashangaki T A L. Structural damage detection of space truss structures using best achievable eigenvectors[J].AIAA Journal, 1994, 32(5): 1049?1057.

[4] Stubbs N, Kim J T. Damage localization in structures without base-line modal parameters[J]. AIAA Journal, 1996, 34(8):1644?1649.

[5] Cornwell P, Doebling S W, Farrar C R. Application of the strain energy damage detection method to plate-like structures[J].Journal of Sound and Vibration, 1999, 224(2): 359?374.

[6] Farrar C R, Jauregui D A. Comparative study of damage identification algorithms applied to a bridge (Ⅰ): Experiment[J].Smart Materials and Structures, 1998, 7: 704?719.

[7] Farrar C R, Jauregui D A. Comparative study of damage identification algorithms applied to a bridge (Ⅱ): Numerical study[J]. Smart Materials and Structures, 1998, 7: 720?731.

[8] Shi Z Y, Law S S. Structural damage localization from modal strain energy change[J]. Journal of Sound and Vibration, 1998,218(5): 825?844.

[9] Jaishi B, Ren W X. Finite element model updating based on eigenvalue and strain energy residuals using multiobjective optimisation technique[J]. Mechanical Systems and Signal Processing, 2007, 21: 2295?2317.

[10] Guan H, Karbhari V M. Improved damage detection method based on element modal strain damage index using sparse measurement[J]. Journal of Sound and Vibration, 2008, 309(3/5):465?494.

[11] Bakhtiari-Nejad F, Rahai A, Esfandiari A. A structural damage detection method using static noisy data[J]. Engineering Structures, 2005, 27(12): 1784?1793.

[12] Yeo I, Shin S, Lee H S. Statistical damage assessment of framed structures from static responses[J]. Journal of Engineering Mechanics, ASCE, 2000, 126(4): 414?421.

[13] 顏王吉. 單元模態應變能靈敏度及其在結構損傷識別中的應用[D]. 長沙: 中南大學土木建筑學院, 2008: 15?21.

YAN Wang-ji. Sensitivity study of element modal strain energy and its application in structural damage detection[D]. Changsha:Central South University. School of Civil Engineering and Architecture, 2008: 15?21.

[14] XIA Yong, HAO Hong. Statistical damage identification of structures with frequency changes[J]. Journal of Sound and Vibration, 2003, 263(4): 853?870.

[15] REN Wei-xin Singular value decomposition based truncation algorithm in solving the structural damage equations[J]. Acta Mechanica Solida Sinica, 2005, 18(2): 181?188.

(編輯 趙俊)

Statistical damage identification of structures based on element modal strain energy sensitivity

YAN Wang-ji, HUANG Tian-li, REN Wei-xin

(School of Civil Engineering and Architecture, Central South University, Changsha 410075, China)

A statistical damage identification algorithm based on element modal strain energy sensitivity was developed to account for uncertainties existing in the structural model and measured vibration data. Firstly, an element modal strain energy-based damage detection method was proposed for detecting damage location and severity. Then the statistics of the structural stiffness parameters in the damaged state were estimated by the perturbation method. The probability of damage existence was estimated based on the probability density functions of the structural stiffness parameters in the intact state and damaged state. The presented technique was applied to detect damages in a numerical simply-supported beam. The results show that a higher probability statistically implies a more likelihood of damage occurrence. The probability of damage unit is larger than that of non-damage unit; and the probability increases with the increase of damage level while it decreases with the increase of noise level.

sensitivity; modal strain energy; modal analysis; damage detection; statistical method

TU311.3

A

1672?7207(2011)01?0152?06

2010?01?10；

2010?04?20

國家自然科學基金資助項目(51078357，50708113)；國家“863”計劃項目(2009AA11Z101)；中國博士后基金資助項目(2008043152)

黃天立(1977?)，男，湖南長沙人，博士后，從事橋梁結構系統識別及健康監測研究；電話：13787150846；E-mail: htianli@mail.csu.edu.cn