基于設計靈敏度分析的圓柱殼聲輻射優化

劉寶山， 趙國忠， 王 劍

（1.大連理工大學工業裝備結構分析國家重點實驗室，遼寧大連 116024；2.中國石油大學儲運與建筑工程學院，山東青島 266555；3.大連交通大學交通運輸工程學院，遼寧大連 116028）

0 引 言

圓柱殼體結構振動引起的聲輻射問題一直是人們所關注的.文獻［1］用解析法和數值法研究了無界非黏滯性重流體中薄圓柱殼的聲振特性，并且用解析法來驗證數值法（有限元法、邊界元法等）的有效性；文獻［2］推導出了水中有限長加肋圓柱殼體的振動和聲輻射的近似解析解；文獻［3］研究了在內壁簡諧法向線力激勵下的水中彈性圓柱殼的振動和聲輻射問題，這有助于深入分析和認識水中結構的聲輻射機理，同時驗證了水下結構共振聲輻射理論；文獻［4］利用有限元軟件（ANSYS）和邊界元軟件（SYSNOISE）對一雙層加肋圓柱殼的水下受激振動與聲輻射作了數值計算分析研究；文獻［5］研究了不同激勵力對流場中敷設阻尼材料的有限長加筋雙層圓柱殼的振動和聲輻射性能的影響；文獻［6］用有限元法、邊界元法和統計能量分析法并結合軟件（ANSYS、SYSNOISE和AUTOSEA）對圓柱殼體在流場中受激振動及聲輻射效率做了數值計算分析研究；文獻［7］結合有限元法和邊界元法分析了深水中復合材料橢圓柱殼的聲輻射；文獻［8］用能量法預測縱向加肋圓柱殼的模態密度、聲輻射效率；文獻［9］從Flügge薄殼理論和Helmholtz波動方程出發，根據模態疊加原理推導了有限長加筋圓柱殼受機械力和內部聲源簡諧激勵下的“內部聲腔－加筋柱殼－外部聲場”耦合方程，比較了點力和點聲源作用時圓柱殼的聲輻射特性以及傳遞損失；文獻［10］考慮雙層殼間環形實肋板之間的耦合作用，以及殼間水層、實肋板與內外殼體的耦合作用，建立了有限長加肋圓柱殼體的振動聲輻射模型.

近十幾年來，如何有效地降低圓柱殼體結構振動和聲輻射得到越來越多的關注.文獻［11］對外部單極子激勵下圓柱殼內部噪聲最小化進行了比較系統的研究；文獻［12］通過向殼體合適的部位添加集中質量改變結構的模態，以達到降低殼體結構聲輻射功率的目的；文獻［13］通過優化鋪層角度，對復合材料圓柱殼結構的內部聲學問題進行了優化研究，經過15次迭代，內部平均噪聲水平降低了2 d B；文獻［14、15］研究了外部聲源激勵下夾心圓柱殼聲傳輸和聲輻射優化問題.本文提出圓柱殼體結構振動聲輻射優化模型，尋求優化方法降低結構輻射噪聲水平.其中，聲輻射功率作為目標函數，圓柱殼體的厚度作為設計變量（分為縱向和環向兩種情況），殼體結構的質量、基頻以及殼體結構內部所計算場點聲壓的平均聲壓作為約束條件.

1 理論基礎

1.1 結構有限元計算

結構在簡諧激勵下的振動方程如下式所示：

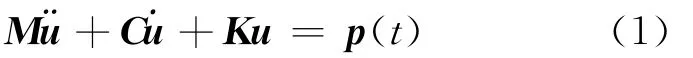
式中：M、K分別為結構的質量矩陣和剛度矩陣；C是結構阻尼矩陣；u是結構位移矢量；p（t）是由外加動荷載引入的簡諧激勵，不妨設p（t）＝phcos（ωt），ω是激勵的角頻率.該方程利用振型疊加法求解，得

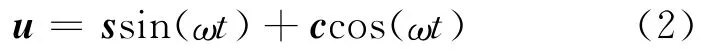
其中s和c是結構模態的線性組合.

求得結構位移響應，對其進行轉換即可得結構表面法向速度：

其中T為轉換矩陣，僅與結構表面形狀有關.

1.2 聲學邊界元計算

1.2.1 邊界元法 封閉結構振動的聲場計算問題如圖1所示.基于Helmholtz積分方程的直接

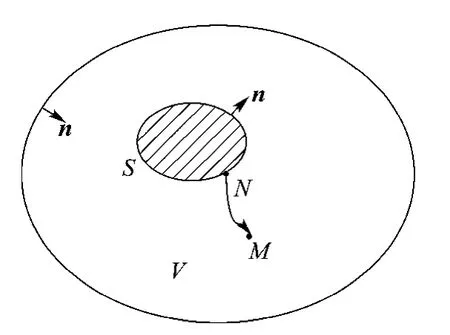
圖1 結構聲輻射示意圖Fig.1 Display of structural acoustic radiation

邊界元方程如下：

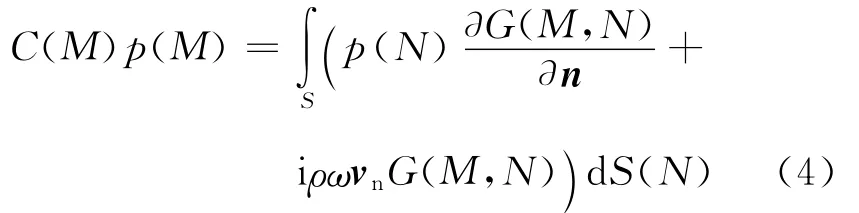
式中

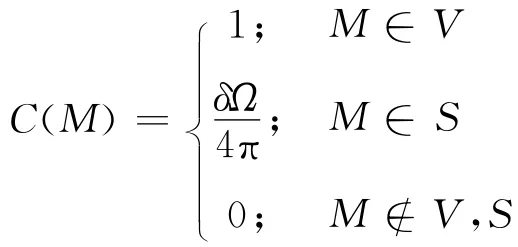
其中δΩ是當點M在結構表面S上時的表面角；i2＝－1；ρ是流體介質的密度；p（M）代表場點M上的聲壓；p（N）代表結構表面點N上的聲壓；vn代表結構表面點N上的法向速度；Helmholtz方程的基本解，即自由空間格林函數

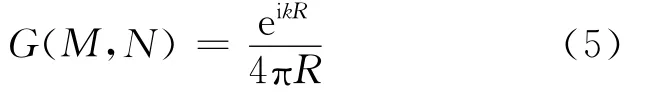
其中R＝｜M－N｜，為場點M到結構表面上點N的距離；k＝ω／c，是波數，c為流體中聲傳播速度.

直接邊界元法中，如果場點位于結構表面上，則形成表面節點聲壓和表面節點法向速度的方程：

式中：H和G是與頻率以及結構表面形狀有關的矩陣，這兩個矩陣是不對稱復數滿秩矩陣，由格林函數積分以及格林函數的導數積分得到.

其中Z＝HTG，是結構的阻抗矩陣.

在已知結構表面聲壓和法向速度的情況下，其結構外部聲場的場點聲壓

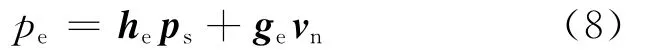
he和ge是從式（4）右邊求得的影響系數，其聲壓的分貝表示形式為

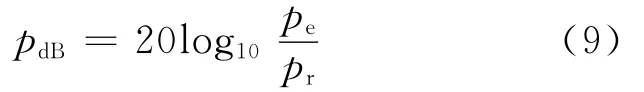
其中pr＝2×10－5Pa，是空氣中的參考聲壓.

定義內部場點平均聲壓

其中Nf是內部場點個數，p j是殼體內部場點聲壓振幅.

1.2.2 聲輻射功率 聲輻射功率是結構表面聲強度的積分［16］，如下式所示：

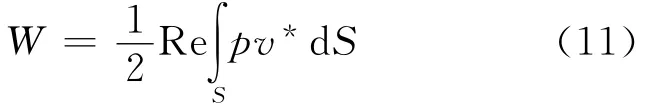
式中：＊代表復共軛.結構表面S離散成Ne個單元后，聲輻射功率為

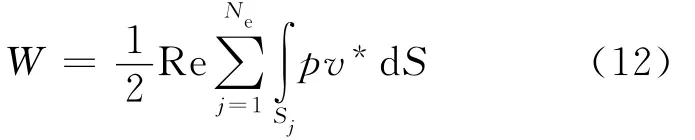
基于式（12）的聲功率計算已經考慮了單元的耦合作用［17］，當單元尺寸比較小時，可以認為每個單元是一個單極子，式（12）可以簡化為

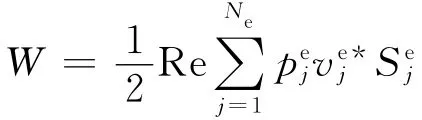
其中＝NTp j是單元聲壓，取插值后的單元中心點聲壓；＝NTv j，是單元速度，同樣是取插值后單元的中心點速度，N是插值函數；p j和v j是單元j上所有節點的聲壓和速度；Sj是單元j的面積.

通過插值函數處理后，聲輻射功率可表示為

式中：B是Hermitian矩陣，與插值函數、激勵頻率以及結構的表面形狀有關.聲輻射功率分貝形式為

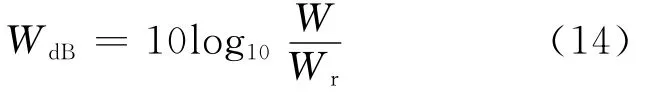
其中Wr＝10－12W，是參考聲輻射功率.

2 優化模型及求解方法

結構優化設計問題［18］表示為如下的一般形式：

其中f（x）為目標函數，n為設計變量x i個數，m為約束函數g j（x）個數，x iu和x il分別為設計變量x i的上界和下界.本文中，圓柱殼體的聲輻射功率作為優化目標，殼體厚度作為設計變量，約束函數中既考慮了結構的指標——質量和基頻，又考慮了聲場性質參數——內部場點平均聲壓.其求解方法見文獻［19］.

3 靈敏度分析

結構響應靈敏度及結構表面法向速度靈敏度分析見文獻［19］.聲壓與聲功率靈敏度分析如下.

3.1 表面聲壓靈敏度

對式（7）求導得結構表面聲壓對于設計變量的靈敏度公式：

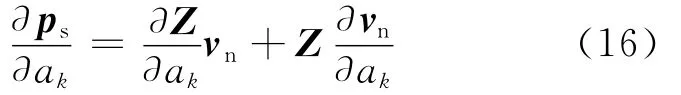
其中ak是第k個設計變量；Z由激勵頻率和結構表面形狀決定，激勵頻率是由荷載決定的，與尺寸變量無關.因此，對于尺寸變量，式（16）右端第一項近似為0，式（16）可簡化為

3.2 場點聲壓靈敏度

對式（8）求導得場點聲壓對于設計變量的靈敏度分析：

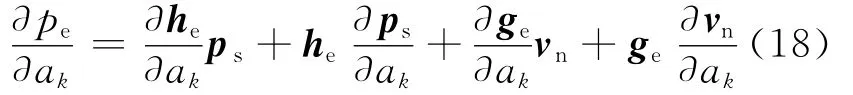
同理，對于尺寸變量，上式可以簡化為

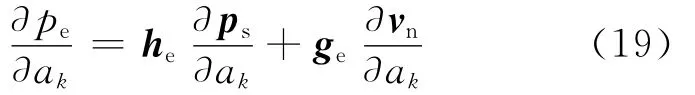
其分貝表示形式可通過對式（9）求導得：

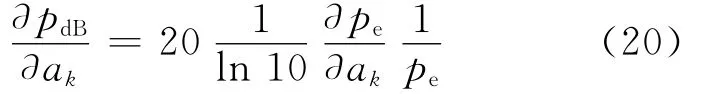
而內場平均聲壓靈敏度可以通過對式（10）求導得：

3.3 聲功率靈敏度

聲輻射功率對設計變量的靈敏度分析通過對式（13）求導得：

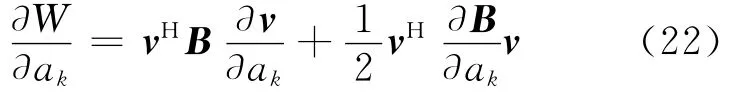
對于尺寸變量，上式同樣可以簡化為

其分貝表示形式為

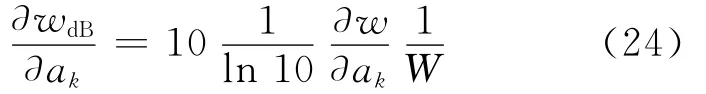
綜上所述，在完成了結構和聲場靈敏度分析之后，即可以求出表面聲壓、場點聲壓、內部場點平均聲壓以及聲輻射功率對于圓柱殼體尺寸設計變量的靈敏度.

4 靈敏度計算及驗證

封閉圓柱殼體結構如圖2所示，其幾何屬性：長度L＝3.0 m，直徑D＝1.0 m；材料屬性：彈性模量E＝6.9×1010Pa，泊松比μ＝0.3，密度ρ＝2.7×103kg／m3；激勵參數：對稱激勵力F處于圖2所示位置，大小為100 N，頻率為120 Hz；邊界條件：兩端完全簡支；聲學參數：空氣密度ρa＝1.21 kg／m3，空氣中聲速c0＝343 m／s.結構有限元模型由兩端的200個四邊形單元和側面的1 600個四邊形單元組成.在邊界元分析中，網格尺寸需要滿足1／6波長要求.本例中，結構的有限元網格同時也是聲學邊界元網格，滿足這一要求.優化模型如圖3所示，殼體結構側面的1 600個單元厚度作為設計變量，兩種厚度分布情況：20個縱向厚度設計變量，沿著環向均勻分布；20個環向厚度設計變量，沿著軸向均勻分布.圓柱殼體厚度t＝2×10－3m，差分步長Δt＝2×10－5m.圓柱殼體內部所計算的場點分布情況如圖4所示，共有40個場點，呈圓柱形分布，直徑d＝0.6 m.

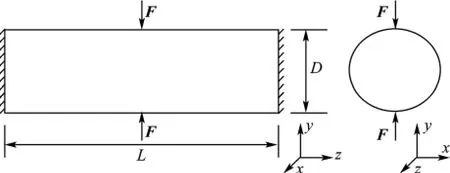
圖2 封閉圓柱殼體結構Fig.2 Closed cylindrical structure

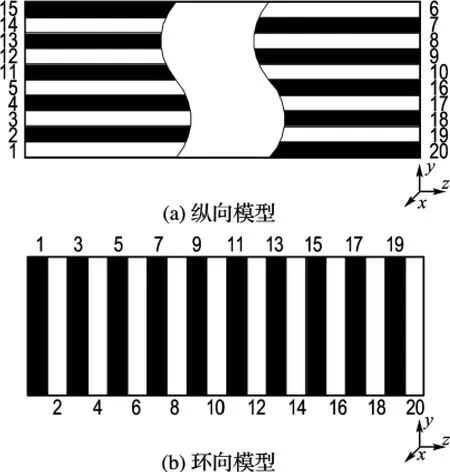
圖3 設計變量分布情況Fig.3 Distribution of design variables

圖4 殼體內部場點分布Fig.4 Distribution of interior field points

本文計算的聲輻射功率靈敏度與差分法計算結果的比較如圖5所示.從圖中可以看出，本文計算的靈敏度與差分法計算的靈敏度吻合得非常好，說明本文的聲輻射功率靈敏度計算是準確的.本文計算的內部場點平均聲壓靈敏度與差分法結果比較如圖6所示.從圖中可以看出，本文計算的靈敏度結果與差分法計算的靈敏度吻合得也非常好，這進一步說明本文的靈敏度計算結果是準確的.從圖5和圖6比較可以看出，聲輻射功率和內部場點平均聲壓對于縱向厚度設計變量靈敏度的趨勢是一致的；而聲輻射功率和內部場點平均聲壓對于環向厚度設計變量靈敏度有所不同，中間部分不一致.

圖5 聲輻射功率靈敏度比較Fig.5 Comparison of sensitivity of acoustic radiation power

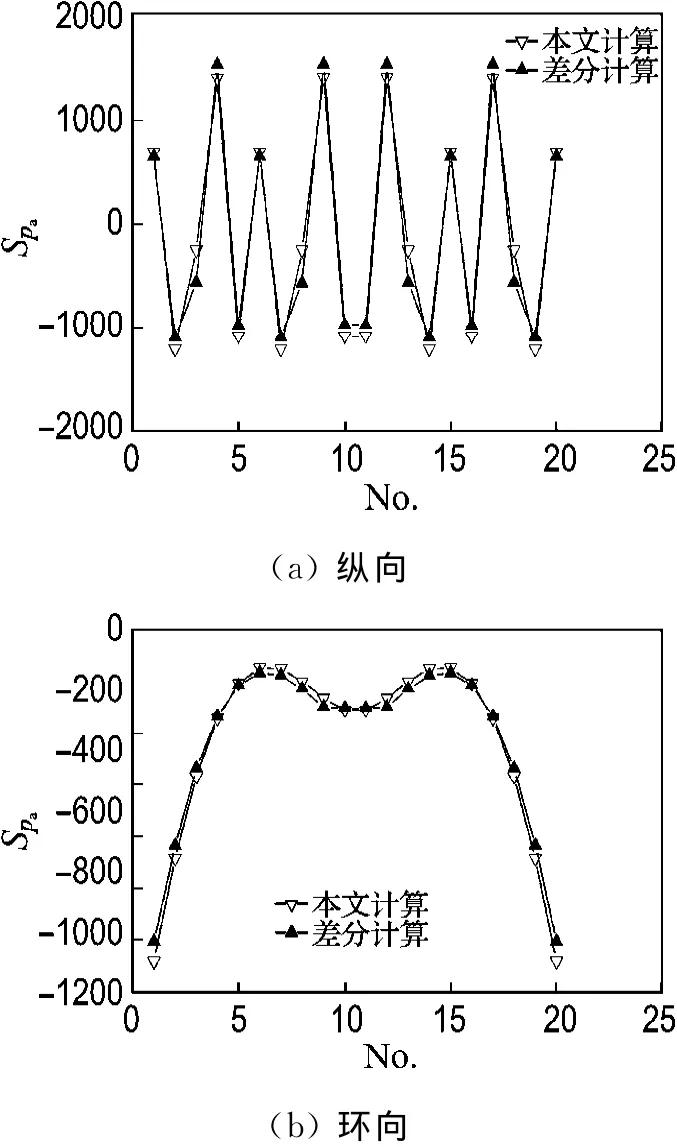
圖6 內部場點平均聲壓靈敏度比較Fig.6 Comparison of sensitivity of average pressure of interior field points

5 數值算例及結果分析

5.1 算例1

模型數據與靈敏度驗證算例相同.20個縱向的殼體厚度設計變量如圖3（a）所示.初始厚度均為2×10－3m，其中上限為3×10－3m，下限為1×10－3m.目標函數迭代過程如圖7所示，經過12次迭代，優化結果收斂.優化模型和結果如表1所示.在滿足約束條件的情況下，聲功率從103.33 d B降到72.35 d B，減少了30.98 d B，優化效果非常明顯.優化后的厚度如圖8所示.從圖中可以看出優化后的厚度分布與初始靈敏度結果圖5（a）相對應.在優化過程中，如果變量的靈敏度正負號不變，那么靈敏度為正時，優化后的設計變量減小；靈敏度為負時，優化后的設計變量增大.

圖7 聲輻射功率優化迭代過程（算例1）Fig.7 Iteration history of acoustic radiation power（Example 1）

表1 縱向厚度優化模型及優化結果Tab.1 Design optimization model for longitudinal thickness and optimized results

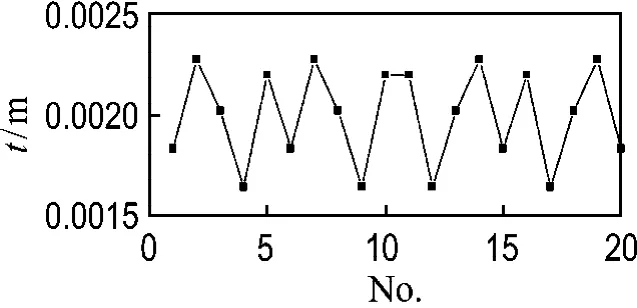
圖8 優化后厚度（算例1）Fig.8 Optimized thickness（Example 1）

5.2 算例2

模型數據與靈敏度驗證算例相同.20個環向的殼體厚度設計變量如圖3（b）所示.初始厚度均為2×10－3m，其中上限為3×10－3m，下限為1×10－3m.目標函數迭代過程如圖9所示，經過6次迭代，優化結果收斂.優化模型及結果如表2所示.在滿足約束條件的情況下，聲功率從103.33 dB降到100.02 dB.優化后的厚度如圖10所示.從圖中可以看出殼體兩端變厚，而中間變薄，這與文獻［11］中結果相似，說明結構聲輻射特性在某種意義下與其聲傳輸特性是相呼應的.

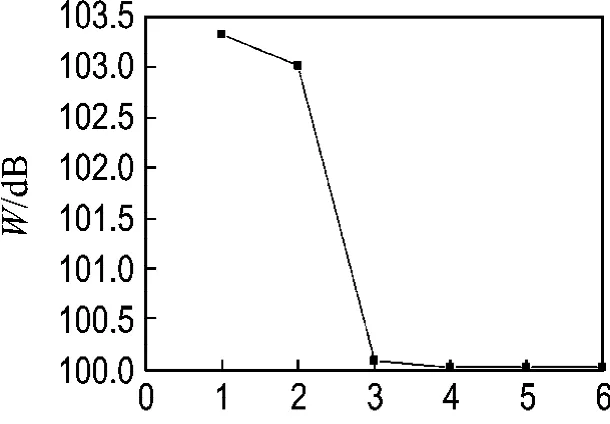
圖9 聲輻射功率優化迭代過程（算例2）Fig.9 Iteration history of acoustic radiation power（Example 2）

表2 環向厚度優化模型及優化結果Tab.2 Design optimization model for circumferential thickness and optimized results

圖10 優化后厚度（算例2）Fig.10 Optimized thickness（Example 2）

從靈敏度的算例中可以看出，兩者的靈敏度差異非常大，縱向變量中靈敏度的正值和負值的絕對值比較大，對聲輻射功率影響大的設計變量的個數也比較多（靈敏度絕對值500之外的有12個），縱向設計變量的變化對聲輻射功率影響比較大.而環向變量中靈敏度的正值比較小，對聲輻射功率影響大的設計變量的個數也比較少（靈敏度絕對值500之外的有4個），環向設計變量的變化對聲輻射功率的影響比較小.因此，縱向厚度設計變量優化后，聲輻射功率降低得多；而環向設計變量優化后，聲輻射功率降低得少.

6 結 語

本文對圓柱殼體聲輻射特性以及優化進行了研究.提出了圓柱殼體結構聲輻射優化模型，即將圓柱殼體的縱向厚度和環向厚度作為設計變量，聲輻射功率作為目標函數，圓柱殼體的質量、基頻、內場平均聲壓作為約束函數.給出了目標函數和約束函數的靈敏度分析公式，并驗證了靈敏度的準確性.從算例中可以看出，縱向厚度和環向殼體厚度優化均可以有效地降低殼體結構的聲輻射，從某種意義上講，這預示著圓柱殼體可通過縱向加肋或者環向加肋以達到降低結構聲輻射的目的.對于加肋殼體聲輻射的優化研究是作者的后續工作.

［1］BEROT F，PESEUX B.Vibro－acoustic behavior of submerged cylindrical shells：Analytical formulation and numerical model［J］.Journal of Fluids and Structures，1998，12（8）：959－1003

［2］湯渭霖，何兵蓉.水中有限長加肋圓柱殼體振動和聲輻射近似解析解［J］.聲學學報，2001，26（1）：1－5

［3］劉 濤，范 軍，湯渭霖.水中彈性圓柱殼的共振聲輻射［J］.聲學學報，2002，27（1）：62－66

［4］商德江，何祚鏞.加肋雙層圓柱殼振動聲輻射數值計算分析［J］.聲學學報，2001，26（3）：193－201

［5］陳美霞，駱東平，王祖華，等.激勵力對雙層圓柱殼聲輻射性能的影響［J］.船舶力學，2005，9（2）：124－130

［6］賀 晨，盛美萍，石煥文，等.圓柱殼體振動聲輻射效率數值計算分析［J］.噪聲與振動控制，2006，26（4）：51－54

［7］倪 樵，艾國慶.深水復合材料圓柱殼聲輻射的數值分析［J］.華中科技大學學報，2006，34（12）：77－79

［8］RAMACHANDRAN P，NARAYANAN S.Evaluation of modal density，radiation efficiency and acoustic response of longitudinally stiffened cylindrical shell［J］.Journal of Sound and Vibration，2007，304（1－2）：154－174

［9］彭 旭，關姍姍，駱東平，等.內部聲激勵下加筋圓柱殼的聲輻射特性分析［J］.固體力學學報，2007，28（4）：355－361

［10］吳培榮，范 軍.有限長雙層加肋圓柱殼體的聲輻射特性［J］.船舶工程，2009，31（4）：13－15

［11］CRANE S P，CUNEFARE K A，ENGELSTAD S P，etal.Comparison of design optimization formulations for minimization of noise transmission in a cylinder［J］.Journal of Aircraft，1997，34（2）：236－243

［12］CONSTANS E W，BELEGUNDU A D，KOOPMANN G H.Design approach for minimizing sound power from vibrating shell structures［J］.AIAA Journal，1998，36（2）：134－139

［13］JOHNSON W M，CUNEFARE K A.Structural acoustic optimization of a composite cylindrical shell using FEM／BEM［J］.Journal of Vibration and Acoustics，2002，124（7）：410－413

［14］DENLI H，SUN J Q.Structural－acoustic optimization of sandwich structures with cellular cores for minimum sound radiation［J］.Journal of Sound and Vibration，2007，301（1－2）：93－105

［15］DENLI H，SUN J Q.Structural－acoustic optimization of sandwich cylindrical shells for minimum interior sound transmission［J］.Journal of Sound and Vibration，2008，316（1－5）：32－49

［16］SNYDER S D，TANAKA N.Calculating total acoustic power output using modal radiation efficiencies［J］.Journal of the Acoustical Society of America，1995，97（3）：1702－1709

［17］CUNEFARE K A，KOOPMANN G H.Acoustic design sensitivity for structural radiators［J］.Journal of Vibration and Acoustics，1992，114（2）：178－186

［18］TOROPOV V V.Simulation approach to structural optimization［J］.Structural and Multidisciplinary Optimization，1989，1（1）：37－46

［19］劉寶山，趙國忠，顧元憲.復合材料層合板結構振動聲輻射優化［J］.振動與沖擊，2008，12（27）：31－35