鋼管自應力混凝土短柱長期荷載作用下變形性能研究
常 旭, 黃承逵
(1.河南理工大學土木工程學院,河南焦作 454000;2.大連理工大學海岸和近海工程國家重點實驗室,遼寧大連 116024)
0 引 言
鋼管自應力混凝土是利用自應力膨脹混凝土代替普通混凝土澆筑于鋼管內而形成的一種新型結構.膨脹混凝土因膨脹受到鋼管限制而在混凝土內產生一種化學預應力,與普通鋼管混凝土結構相比,核心混凝土在承載之前就處于三向應力狀態,有效約束了混凝土在承載中前期的橫向變形并提高了構件的極限承載力[1、2].與普通鋼管混凝土結構相比,鋼管自應力混凝土構件中,核心混凝土受到的約束作用在承載之初就存在,約束效應要好于普通鋼管混凝土結構,但同時也承受了軸向初應力,這樣勢必會造成徐變變形增大,對構件承載力造成不利影響.可見,鋼管自應力混凝土構件徐變變形要更為復雜一些.
1 試驗概況
本次試驗采用的水泥為硫鋁酸鹽自應力水泥.鋼管的屈服強度為341 MPa.部分試件的幾何尺度等參數如表1所示.在鋼管的中部軸向和環向分別對稱貼了4個電阻應變片來測量鋼管自應力混凝土的膨脹變形量,采用UCAM數據采集系統對試件進行了連續35 d的變形測量.本次試驗共設計試件20根,其中10根施加長期荷載,另外10根為對比件,只進行一次性加載試驗.
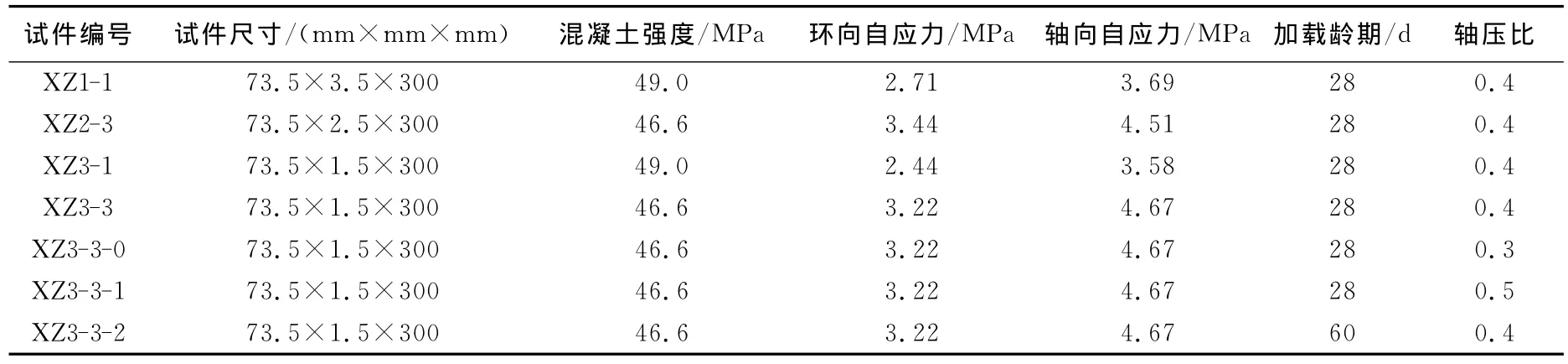
表1 試件一覽表Tab.1 General view of tested specimens
本次試驗采用如圖1所示的加載裝置,其由端板和拉桿組成,端板為250 mm×250 mm×30 mm的鋼板,拉桿直徑為40 mm.在試驗前,先對鋼拉桿力學性能進行標定.在長期持載過程中,主要通過讓拉桿產生相同的變形來確保試件處于軸向受壓狀態.通過擰緊兩端螺母的方式施加荷載,并通過荷載傳感器控制,同時通過鋼拉桿進行校核.持載一段時間后,鋼管混凝土產生徐變變形,鋼拉桿出現松弛現象,要進行不間斷的補載.由于構件持載初期徐變變形較大,最初的兩個月基本上2~3 d需要補載一次.兩個月后基本上一周補載一次.需要指出的是在試驗過程中,試件XZ1-3、XZ2-1上的應變片受到了損害,無法獲得正確的數據;試件XZ3-2測得的數據比較分散,本文在后面的分析中,舍棄了該部分的數據.

圖1 試件加載圖Fig.1 Schematic of specimen loading
2 核心混凝土自應力計算
核心混凝土的膨脹作用可使得鋼管中產生環向和軸向的拉力,如圖2所示.由于采用的是薄鋼管,可以認為環向應力沿管壁厚均勻分布;同時徑向應力因為較小,可以忽略不計.根據實測鋼管的軸向和環向變形,可由式(1)計算出鋼管中產生的環向和軸向應力:
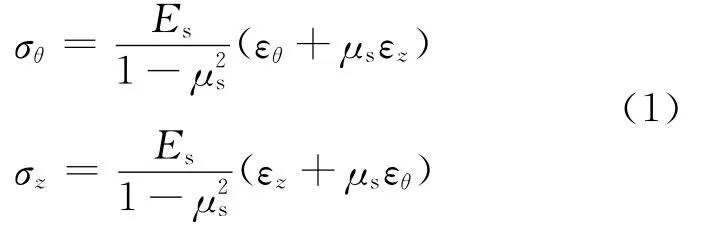
式中:σθ、σz分別為鋼管中產生的環向與軸向應力;εθ、εz分別為試驗測得的鋼管外壁上環向和軸向應變;Es、μs分別是鋼管的彈性模量及泊松比.
按圖2(a)所示平衡條件2σθ·t=2rq,可得

式中:r為鋼管內半徑,t為鋼管壁厚.根據軸向平衡條件As·σz=Ac·σcz,解得

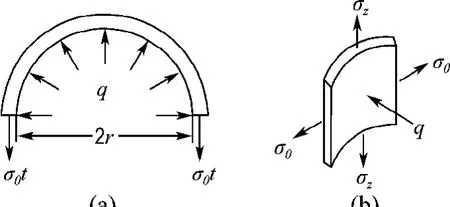
圖2 鋼管受力示意圖Fig.2 Stress of the steel tube
3 徐變計算
3.1 持載后核心混凝土的瞬時應力
對普通鋼管混凝土而言,如果軸壓比不大,可以認為施加長期荷載以后鋼管和混凝土單獨受力,兩者按照各自的剛度分配荷載.對于鋼管自應力混凝土構件而言,鋼管和混凝土在承受荷載之前就產生相互作用,顯然不能按照剛度來分配外荷載,本文參考文獻[3],對持載后鋼管自應力混凝土短柱截面的應力分布規律進行推導.
持載前,鋼管和核心混凝土就相互作用且處于平衡狀態,根據前文分析,可認為鋼管處于平面應力狀態,核心混凝土處于三向受壓狀態.假設施加長期荷載后,鋼管和核心混凝土發生了瞬時變形,鋼管的環向和軸向應力變化量分別為Δσs1、Δσs2,核心混凝土的軸向和徑向應力變化量分別為Δσc1、Δp.由于在本次試驗中,軸壓比都基本在0.4左右,可以假定施加荷載后,鋼管和混凝土均處于彈性狀態,由胡克定律可知,在核心混凝土中:
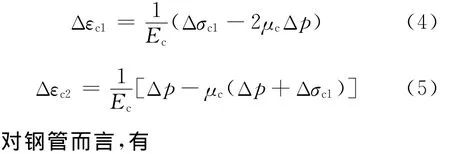
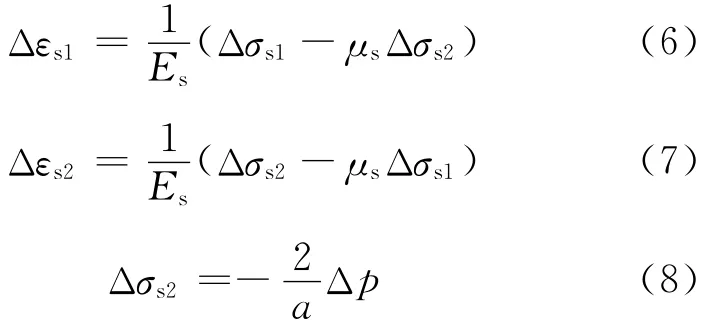
假設施加的長期荷載為N,那么有
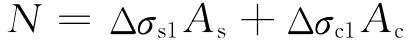
根據軸向和徑向變形協調,有
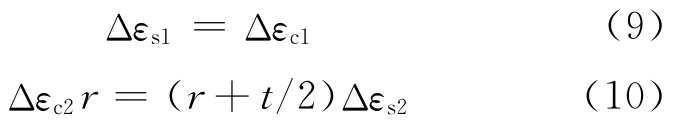
把式(4)~(7)分別代入變形協調條件(9)及(10),并消去Δp,可得
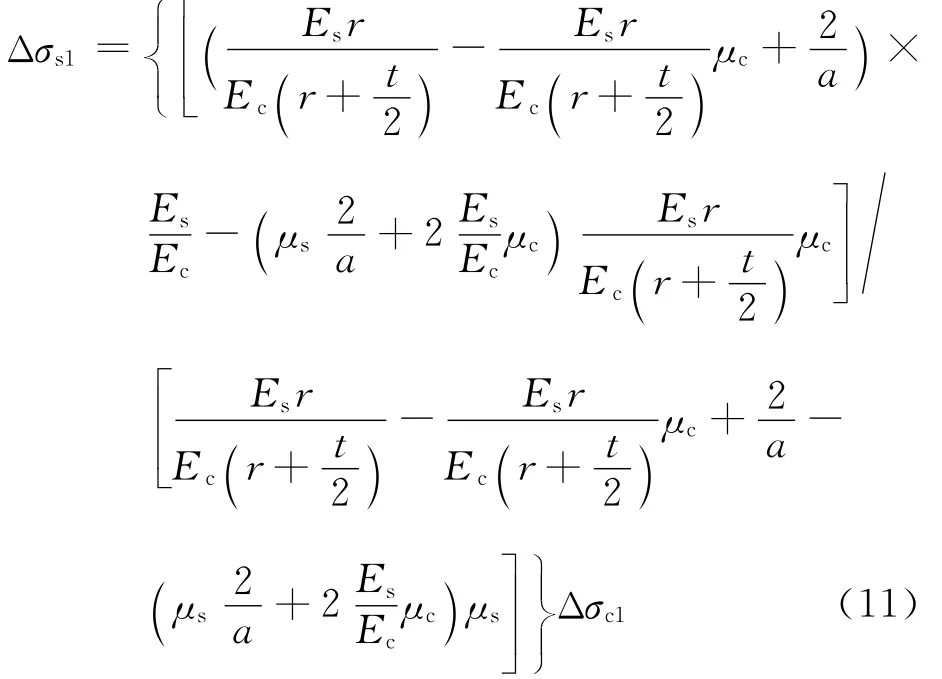
結合平衡條件N=Δσs1As+Δσc1Ac,可以得到持載后,核心混凝土上的瞬時應力變化量Δσc1及Δp.因此,核心混凝土上的瞬時應力可分別由下式表示:
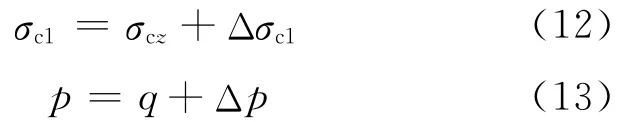
3.2 徐變系數及計算方法的選取
徐變變形的計算主要有兩個方面:徐變系數選取和計算方法的確定.本文的徐變系數采用ACI209委員會推薦的混凝土徐變系數:
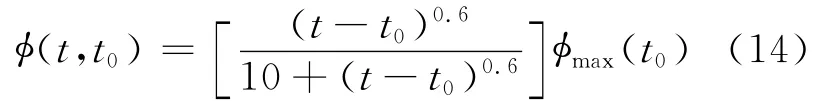
其中max(t0)為徐變的最終值,具體計算參見文獻[4].
關于混凝土徐變變形的計算理論比較多,本文采用齡期調整的有效模量法[4],徐變變形可表達為
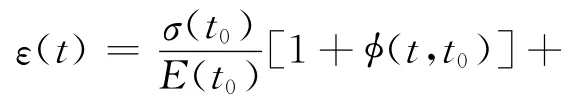
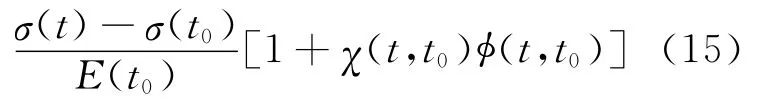
χ(t,t0)為老化系數,按照文獻[5]的統計結果,老化系數可以表示為
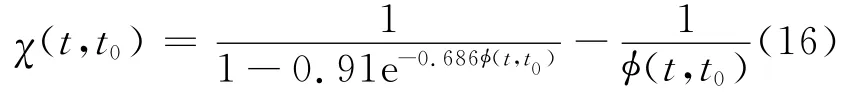
由前文分析可知,核心混凝土處于三向受壓狀態下,按照文獻[6]的方法,可以采用“名義應力”來描述核心混凝土的實際受力大小.核心混凝土的軸向徐變可以表示為
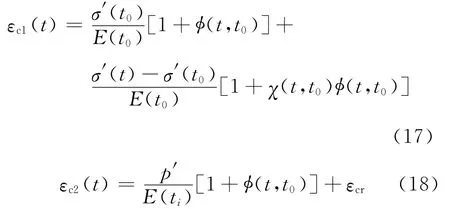
σ′為“名義軸向應力”,具體表達式為

p′為“名義徑向應力”,可用下式表示:
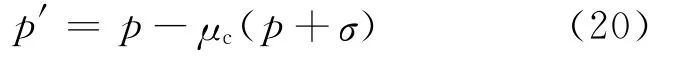
εcr是軸向徐變泊松比引起的變形,可以表示為εcr=μ′c[εc1(ti)-εc1(t0)].
這樣就把采用齡期調整的有效模量法從一維推廣到了三維,可以采用逐步計算的方法來求得徐變變形,具體的計算過程如下:
(1)在齡期t0給出所持荷載的大小,根據上述的計算公式,確定施加外荷載以后鋼管和混凝土的實際應力大小.
(2)ti-1到ti時段內,核心混凝土上的應力變化量為Δσc1,根據ti-1時刻核心混凝土的徑向應力,按照前述計算方法求得核心混凝土在ti-ti-1時間段內所發生的徐變變形量.根據軸向和徑向變形協調條件:Δεc1=Δεs1及Δεc2r=Δεs2(r+t/2),可得鋼管在軸向和環向所產生的應變,最后由胡克定律,可得鋼管內的應力變化量.
(3)由求得的鋼管內的應力及核心混凝土上的應力,判斷是否滿足力的平衡條件:Δσc1Ac=Δσs1As,如果不滿足,需要返回(2)繼續調整Δσc1,直到平衡條件得以滿足.
(4)給定新的時間增量,重復步驟(2)、(3).
按照上述方法,對本次試驗的試件進行了計算,試驗結果和計算結果對比如圖3所示,兩者基本吻合,肯定了上述計算方法的可行性.
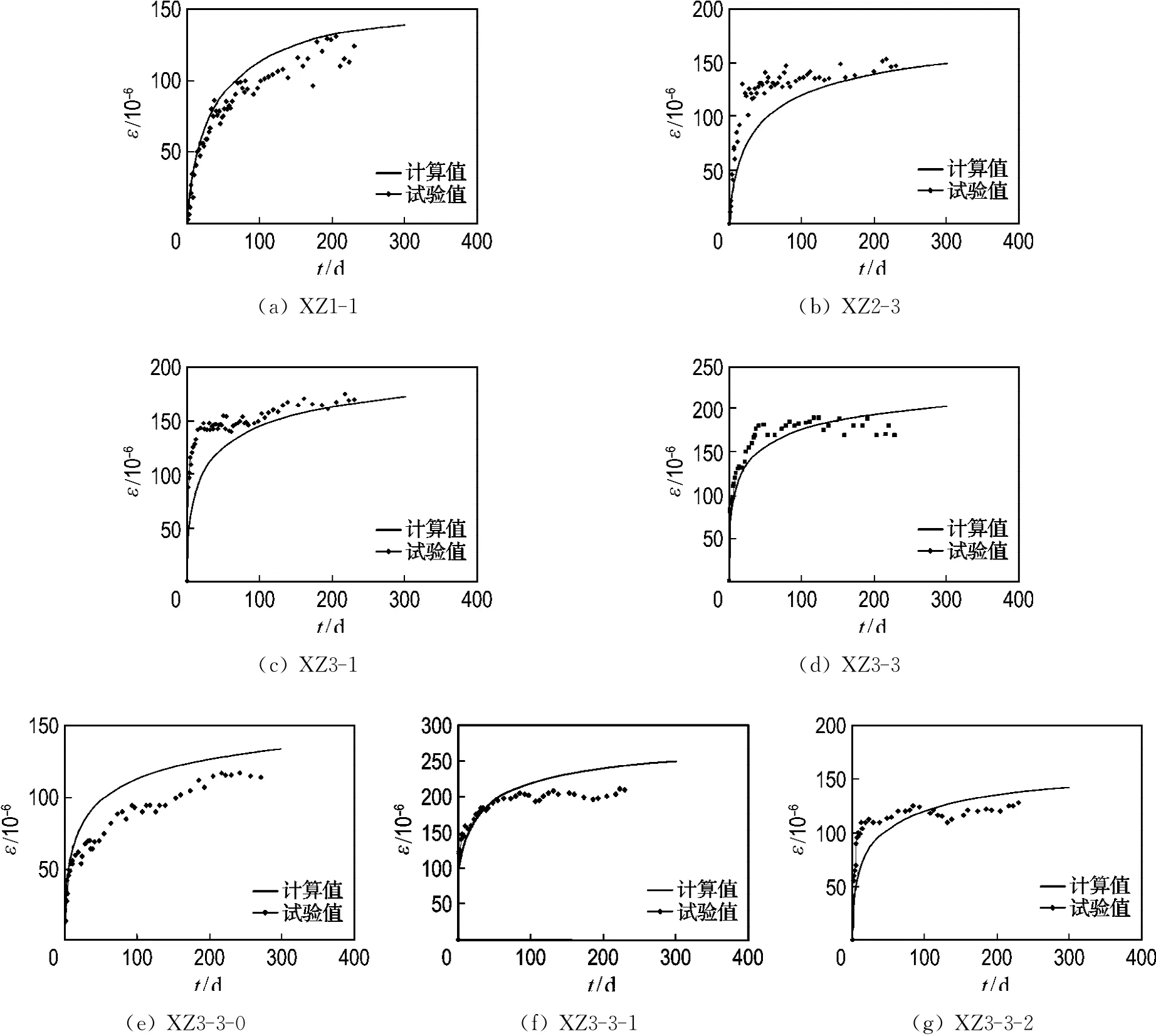
圖3 徐變變形試驗及計算結果對比Fig.3 Creep curves of tested and calculated results
3.3 參數分析
本節對影響鋼管自應力混凝土構件徐變變形的主要因素,如加載齡期、含鋼率、軸壓比和核心混凝土的強度等級[6~8]及初始自應力等進行了分析計算.
軸壓比對徐變變形的影響規律如圖4所示.模型的參數為環向自應力p0=3 MPa,軸向自應力σc10=5 MPa,混凝土為C50,鋼管為Q235鋼,其內徑和壁厚分別為50 mm和3.5 mm.從圖4可知,鋼管自應力混凝土軸壓柱的徐變變形隨著軸壓比的增大而增大.
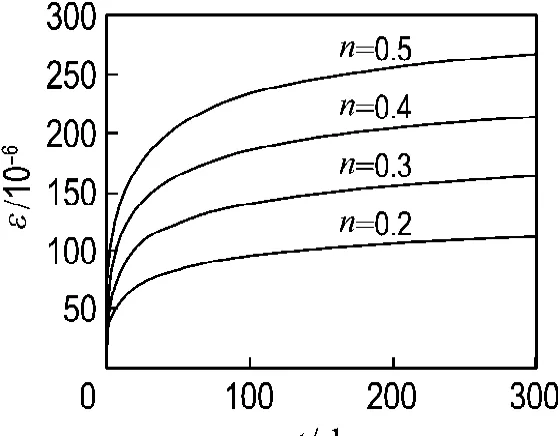
圖4 應力級別對徐變曲線的影響規律Fig.4 Effect of axial load ratios on creep curves
圖5表示加載齡期對鋼管自應力混凝土軸壓柱徐變變形的影響規律.采用的計算參數與上文所述一致,只不過軸壓比為定值0.35;加載齡期為變量,其變化范圍為7~90 d.
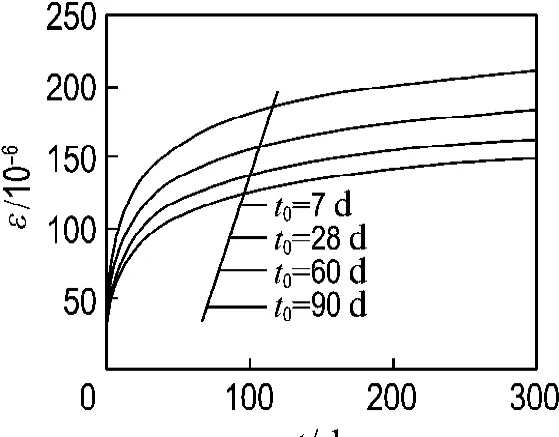
圖5 加載齡期對徐變曲線的影響規律Fig.5 Effect of load age on creep curves
圖6表明鋼管自應力的徐變變形隨著含鋼率的增大而減小.主要是因為含鋼率越大,鋼管對核心混凝土提供的約束強度越高,限制構件軸向變形的發展;同時含鋼率增大,能夠更多地分擔從核心混凝土卸載下來的荷載,從而保持較小的軸向變形.模型的計算參數為軸壓比n=0.35;加載齡期28 d;含鋼率從0.10逐步增加到0.37;其他參數不變.
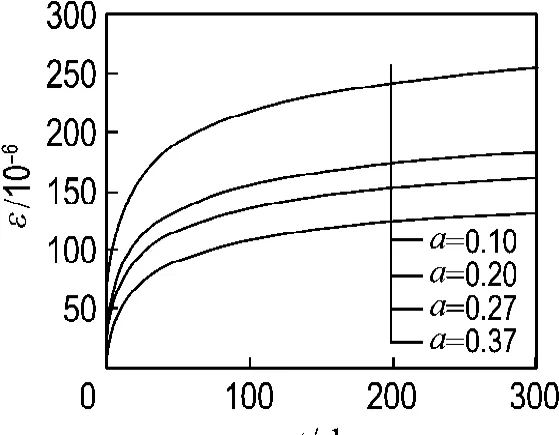
圖6 不同含鋼率對徐變曲線的影響Fig.6 Effect of steel ratio on creep curves
承載前,鋼管和核心混凝土中存在相互作用的自應力,這是其重要的特點.圖7(a)表明,鋼管自應力混凝土的軸向變形是隨著徑向自應力的增大而減小的,可見環向自應力的存在有利于減小軸向徐變.模型的計算參數為軸壓比n=0.35;加載齡期28 d;徑向自應力的變化范圍為0~8 MPa,軸向自應力為0,其他參數與上文采用的計算模型相同.然而鋼管自應力混凝土結構中,不僅存在徑向自應力,并且也存在軸向自應力.從圖7(b)可知,如果考慮了軸向自應力的影響,鋼管自應力混凝土的徐變變形要大于普通鋼管混凝土同類構件.雖然環向自應力可有助于減小軸向徐變,但是由于其同時又要承受一定的軸向初應力,且軸向初應力引起的徐變也要大于環向自應力對徐變的有利影響,所以,鋼管自應力混凝土的徐變變形隨著自應力的增加而增大.根據試驗獲得的初始自應力的規律,圖7(b)中,自應力參數分別為p=0,σc10=0;p=3 MPa,σc10=5 MPa,p=6 MPa,σc10=9 MPa.
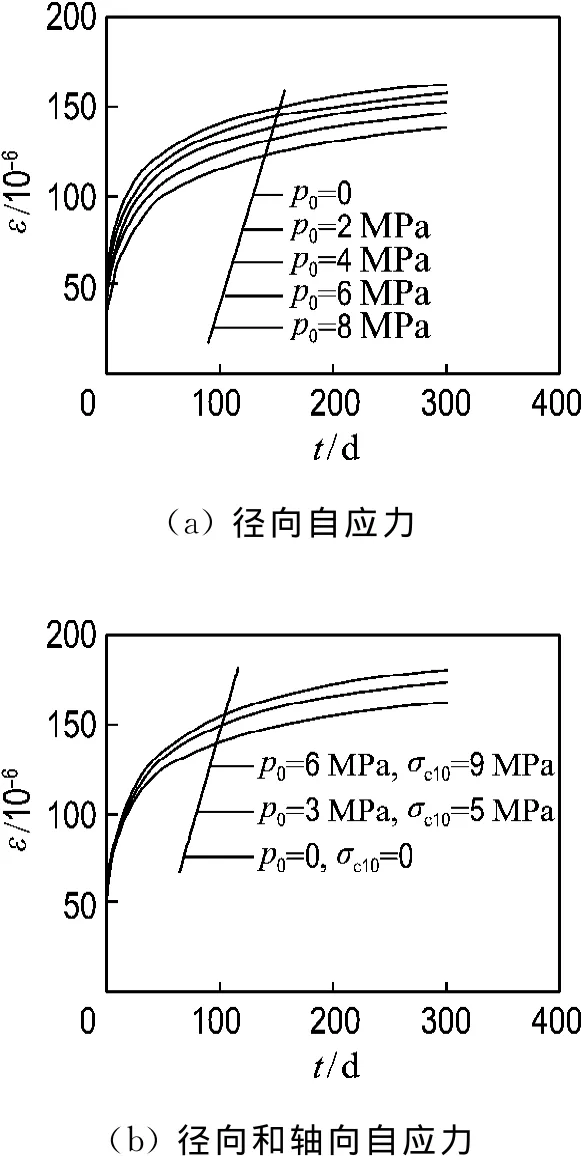
圖7 自應力水平對徐變變形的影響Fig.7 Effect of self-stress on creep curves
4 結 論
(1)與普通鋼管混凝土一樣,軸壓比、含鋼率及加載齡期等對鋼管自應力混凝土徐變變形有明顯的影響;其變形規律與普通鋼管混凝土基本一致.
(2)環向自應力對控制核心混凝土的軸向徐變變形有積極的意義,但實際的鋼管混凝土結構中除了環向自應力外,還要承擔軸向自應力,因此鋼管自應力混凝土軸壓柱的徐變要大于普通鋼管混凝土軸壓柱.
由于鋼管自應力混凝土結構的受力狀態比較復雜,本文的研究結果可為今后進一步研究該結構的性能提供參考.
[1]黃承逵,徐 磊.鋼管自密實自應力混凝土軸壓短柱力學性能研究[J].大連理工大學學報,2006,46(5):696-701
(HUANG Cheng-kui,XU Lei.Research on mechanical performance of self-compacting and selfstressing concrete-filled steel tube short column under axial loading[J].Journal of Dalian University of Technology,2006,46(5):696-701)
[2]徐 磊.鋼管自應力免振混凝土軸壓柱設計理論研究[D].大連:大連理工大學,2006
[3]王元豐,韓 冰.徐變對鋼管混凝土軸心受壓短柱禁錮應力影響分析[J].鐵道學報,2000(S1):92-94
[4]周 履,陳永春.收縮徐變[M].北京:中國鐵道出版社,1994
[5]顧建中,劉西拉.軸向載荷作用下鋼管混凝土的徐變[J].中國公路學報,2001,14(4):59-62
[6]王元豐,韓 冰.鋼管混凝土軸心受壓構件徐變分析[J].中國公路學報,2000,13(2):57-60
[7]韓 冰,王元豐.鋼管混凝土小偏心受壓構件徐變分析[J].工程力學,2001,18(6):110-116
[8]韓林海,楊有福.長期荷載作用對矩形鋼管混凝土軸心受壓柱力學性能的影響研究[J].土木工程學報,2004,37(3):12-18

