一種基于濾波器矩陣的Hammerstein預(yù)失真器
佀秀杰, 金明錄, 劉文龍
(大連理工大學(xué)電子信息與電氣工程學(xué)部,遼寧大連 116024)
0 引 言
現(xiàn)代無線通信為多用戶在同一射頻信道提供高速率的多媒體服務(wù),而這些高質(zhì)量的服務(wù)是以增加信號帶寬為代價的.寬帶信號具有非恒包絡(luò)、高峰均比的特性,這些特性不僅增加了功率放大器(power amplifier,PA)的非線性失真而且使得PA的記憶效應(yīng)不能再被忽視.PA的記憶效應(yīng)給系統(tǒng)引入了更嚴(yán)重的帶內(nèi)和帶外的失真(頻譜間干擾),增加了系統(tǒng)誤碼率和相鄰信道間干擾[1、2].傳統(tǒng)的無記憶預(yù)失真器(predistorter,PD)不能很好地補償帶記憶效應(yīng)PA的非線性,因此對記憶預(yù)失真器的研究成為這一領(lǐng)域的研究熱點.
預(yù)失真技術(shù)是通過在PA前級聯(lián)一個與PA特性(非線性及記憶效應(yīng))相反的PD來達(dá)到線性化目的的,其線性化性能取決于對預(yù)失真器建模的準(zhǔn)確性[3](即對PA逆特性描述的精確程度),以及系統(tǒng)辨識算法的性能.然而,建模的準(zhǔn)確性與系統(tǒng)辨識算法的性能之間存在著制約關(guān)系:如果一味追求對系統(tǒng)行為描述的準(zhǔn)確性就會使模型辨識算法的復(fù)雜度很高;反之,只顧及降低算法的復(fù)雜度則會導(dǎo)致模型對系統(tǒng)行為描述性能的降低.因此,在對PD進行系統(tǒng)建模時需要權(quán)衡兩方面的關(guān)系.需要指出的是,預(yù)失真器建模的一個關(guān)鍵問題是該模型對PA逆記憶特性的描述能力[4、5].
目前,為了補償帶記憶效應(yīng)PA的非線性失真,PD多采用記憶多項式模型[6、7](MPM)和Hammerstein模型[8~10].MPM是由Volterra級數(shù)模型簡化而來,它只保留Volterra級數(shù)核函數(shù)對角線部分.該模型的主要缺點在于對PD記憶效應(yīng)的描述不充分,且保留了Volterra級數(shù)模型只在有限系統(tǒng)輸入幅度范圍內(nèi)收斂的問題.基于Hammerstein模型的PD是由非線性系統(tǒng)級聯(lián)線性系統(tǒng)而成,能夠較準(zhǔn)確地描述PA的逆特性,即能夠較好地補償帶記憶效應(yīng)功率放大器的非線性失真.但是,精確地描述PA逆記憶效應(yīng)和高效的辨識算法是Hammerstein預(yù)失真研究的難點.
針對常用的Hammerstein預(yù)失真器對PA逆特性描述不夠充分且系統(tǒng)辨識困難的問題,Jardin提出用一種濾波器查找表的方法來實現(xiàn)Hammerstein模型中的線性子系統(tǒng),并得到了對帶記憶效應(yīng)PA非線性失真較好的補償性能.在該PD研究基礎(chǔ)上,本文提出改進的Hammerstein預(yù)失真器,重點在于提高對PA記憶效應(yīng)的補償能力,采用復(fù)增益查找表(LUT)級聯(lián)濾波器矩陣作為其實現(xiàn)形式,以有效地補償帶記憶效應(yīng)PA的非線性失真.
1 基于濾波器查找表的預(yù)失真器
Hammerstein模型屬于兩箱結(jié)構(gòu),由一個靜態(tài)非線性子系統(tǒng)級聯(lián)一個線性動態(tài)子系統(tǒng)組成.當(dāng)用Hammerstein模型作為PD的模型時,兩個子系統(tǒng)分別用于補償PA非線性和記憶效應(yīng)引起的失真,即PD應(yīng)具有與PA的非線性和記憶效應(yīng)完全相反的特性.
文獻(xiàn)[8]提出的PD(記為FLUT)由一個復(fù)增益查找表和一個濾波器查找表組成,分別用于實現(xiàn)Hammerstein模型的靜態(tài)非線性子系統(tǒng)和線性動態(tài)子系統(tǒng).FLUT的結(jié)構(gòu)和信號流程如圖1所示,其中z(n)是PD的輸入數(shù)據(jù),zl(n)是LUT模塊的輸出,zlf(n)是PD的輸出,|·|Q表示對數(shù)據(jù)取模并進行量化.FLUT的算法復(fù)雜度低,且能夠較有效地補償帶記憶效應(yīng)功率放大器的非線性失真.
FLUT與一般Hammerstein預(yù)失真器(LUT級聯(lián)一個濾波器)相比,對帶記憶效應(yīng)PA非線性失真補償效果較好的原因在于:Hammerstein模型中線性子系統(tǒng)由一個濾波器查找表來完成,濾波器的選擇與當(dāng)前輸入信號有關(guān),即當(dāng)前輸入信號決定系統(tǒng)采用哪一組濾波器系數(shù)向量,用公式表示為h|xn,其中h是有限沖激響應(yīng)(FIR)濾波器的系數(shù)向量,x n是當(dāng)前輸入信號.

圖1 FLUT PD結(jié)構(gòu)Fig.1 The structure of FLUT PD
2 改進的Hammerstein預(yù)失真器
為更有效地補償PA記憶效應(yīng)引起的失真,本文提出一種基于FLUT改進的Hammerstein預(yù)失真器.該預(yù)失真器中非線性子系統(tǒng)仍采用查找表來描述.查找表中存放的是一組復(fù)增益值G,其尋址是通過對輸入信號幅值進行均勻量化的方法得到.當(dāng)前輸入記作z(n),其信號最大幅值為zmax,如果查找表大小為N,有量化步長q=zmax/(N-1),則LUT索引指針i(n)的值為
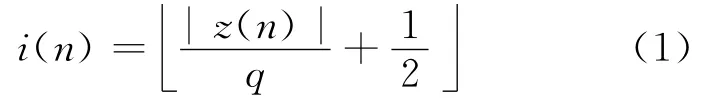
其中表示對x向下取整運算.
根據(jù)得到的索引指針對LUT尋址輸出對應(yīng)當(dāng)前輸入的復(fù)增益值Gi(n),則非線性子系統(tǒng)的輸出
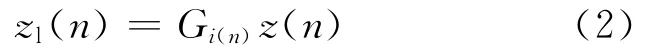
基于對FLUT的研究,濾波器的參數(shù)如果能夠考慮盡可能多的輸入信號,Hammerstein預(yù)失真器對PA的逆記憶效應(yīng)的描述應(yīng)會更精確,即濾波器向量的選擇由輸入序列決定,即h|xn(設(shè)L為預(yù)失真器的記憶長度,那么x n=(x nx n-1…x n-L+1).因為要考慮L個輸入信號的影響,這使得對濾波器系數(shù)向量的索引過于復(fù)雜,同時會引入較多的量化誤差.為了解決上述問題,本文提出用一個N×NFIR的濾波器矩陣來實現(xiàn)Hammerstein預(yù)失真器的線性子系統(tǒng).該矩陣的每一項是一組濾波器系數(shù)向量h i,j,即濾波器系數(shù)向量的選擇僅由兩個與輸入序列有關(guān)的參量決定.因為當(dāng)前輸入信號是最主要且不容忽略的一個影響因子,因此決定濾波器系數(shù)向量選擇的一個參量應(yīng)與當(dāng)前輸入有關(guān).另外,決定濾波器系數(shù)向量選擇的第2個參量應(yīng)與歷史輸入有關(guān),雖然可考慮歷史輸入的總和,但是其不能反映對當(dāng)前輸入的影響,因為系統(tǒng)所要求解的畢竟是對應(yīng)當(dāng)前輸入的有效輸出.因此,歷史輸入需要用一個綜合且合理的變量來表示,本文定義該變量為rn,其表示如下所示:
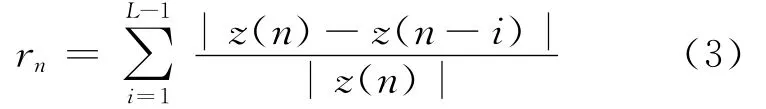
變量rn能定量地表征歷史輸入數(shù)據(jù)對當(dāng)前輸入數(shù)據(jù)的影響.因此,h|被簡化為h|.
濾波器矩陣的索引根據(jù)表項內(nèi)容的影響因子x n和r n進行設(shè)計:第一維索引采用對當(dāng)前輸入信號x n進行均勻量化得到,即采用與非線性部分LUT相同的索引i(n);第二維索引j(n)通過對參數(shù)rn進行均勻量化得到.如果rn的取值范圍是0到最大值rmax,量化步長記為p=rmax/(NFIR-1),則第二維索引j(n)可以表示為
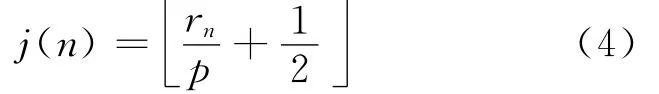
根據(jù)第二維索引確定對應(yīng)于線性系統(tǒng)輸入zl(n)=(zl(n)zl(n-1) …zl(n-L+1))T的 FIR 濾波器系數(shù)向量h i,j=(hi,j(0)hi,j(1) …h(huán)i,j(L-1)),則FIR濾波器的輸出zlf表示如下:
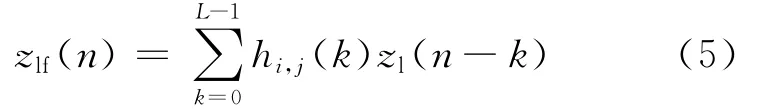
因此,提出的改進Hammerstein預(yù)失真器如圖2所示.圖中,z n-1表示向量(z(n-1)z(n-2) …z(n-L+1)).
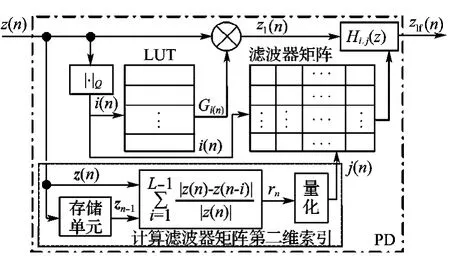
圖2 提出的Hammerstein PD結(jié)構(gòu)Fig.2 The structure of proposed Hammerstein PD
對于本文提出的Hammerstein預(yù)失真器,兩個子系統(tǒng)分別采用直接學(xué)習(xí)結(jié)構(gòu)和非直接學(xué)習(xí)結(jié)構(gòu)[8]對其參數(shù)進行更新.因此,兩個子系統(tǒng)的更新公式分別如式(6)和式(7)所示.
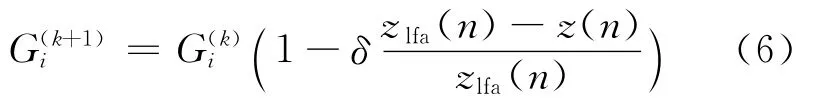
其中zlfa(n)為帶PD的PA(記為PD+PA)的輸出,δ是自適應(yīng)步長.
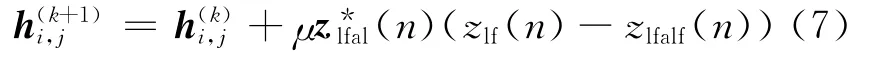
其中h i,j=(hi,j(0)hi,j(1) …h(huán)i,j(L-1)),zlfal(n)=(zlfal(n)zlfal(n-1) …zlfal(n-L+1))T是非直接學(xué)習(xí)結(jié)構(gòu)中后失真器LUT部分的輸出向量,zlfalf(n)是非直接學(xué)習(xí)結(jié)構(gòu)中后失真器當(dāng)前時刻的輸出,μ是自適應(yīng)步長.
3 仿真實驗及分析
為驗證所提出的Hammerstein預(yù)失真器的有效性,對該PD進行仿真.PA模型采用只有奇數(shù)階的記憶多項式模型,其記憶長度為M,階為P.在時刻n,PA的輸出可以表示為

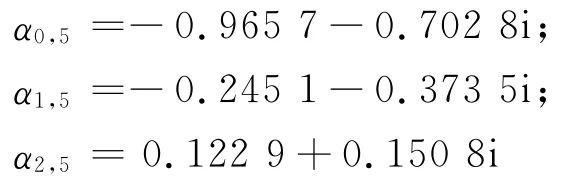
系統(tǒng)輸入采用16QAM調(diào)制信號,并通過升余弦滾降濾波器進行波形成形,其參數(shù)分別為滾降系數(shù)0.5,延遲3,升采樣率8.對成形后的信號進行歸一化處理,使得輸出采樣值的最大包絡(luò)值為1,并進行峰值回退PBO處理,PBO值為0.98.
仿真實驗中,設(shè)LUT的大小N為64;對于濾波器矩陣,其行數(shù)由N確定,而列數(shù)NFIR設(shè)為4,另外,F(xiàn)IR濾波器長度L設(shè)為4.
自適應(yīng)更新PD系數(shù)的步長設(shè)置如下:對LUT,δ(6)為0.1;對濾波器矩陣中FIR濾波器更新,設(shè)其自適應(yīng)步長μ(7)為0.01.
PD初始化如下:LUT表項中的內(nèi)容初始化為1,F(xiàn)IR濾波器的沖激響應(yīng)初始化為單位脈沖.
仿真采用文獻(xiàn)[8]中的更新方法,即開始時先用有限采樣點僅對非線性子系統(tǒng)進行更新(本次實驗采用500個采樣點),然后對線性子系統(tǒng)進行更新,同時更新非線性子系統(tǒng).圖3是本文提出的PD級聯(lián)PA系統(tǒng)的均方誤差(MSE,Ems)曲線,本文提出的PD記為“LFM”.與傳統(tǒng)的Hammerstein預(yù)失真器(簡記為H-PD)相比,其系統(tǒng)誤差減小了大約7 dB.需要指出的是:仿真實驗中,H-PD中濾波器長度L為16;為了能夠清晰地對比各方法的效果,對本文中的MSE曲線進行了平滑處理.

圖3 LFM+PA與H-PD+PA系統(tǒng)的MSE曲線Fig.3 The MSE curves of LFM+PA and H-PD+PA systems
由圖4可以看出:(1)3種預(yù)失真系統(tǒng)的MSE曲線均低于傳統(tǒng)H-PD系統(tǒng)的MSE曲線,說明考慮濾波器參數(shù)向量與輸入序列有關(guān)的合理性;(2)x LFM+PA和LFM+PA系統(tǒng)的MSE曲線都低于FLUT+PA系統(tǒng)MSE曲線,說明考慮更多的輸入數(shù)據(jù)對濾波器的影響的合理性,以及rn定義的合理性.同時,需要注意到的兩點是:(1)x LFM+PA和LFM+PA系統(tǒng)的MSE曲線幾乎重合;(2)本文提出的x LFM+PA和LFM+PA系統(tǒng)在初始階段誤差較FLUT+PA系統(tǒng)大,且收斂速度也受到了一定的影響.第1個現(xiàn)象出現(xiàn)的原因是,采用的PA模型僅兩個記憶長度,記憶效應(yīng)不強,且訓(xùn)練序列長度足夠長;第2個現(xiàn)象出現(xiàn)的原因是,x LFM+PA和LFM+PA系統(tǒng)中濾波器組很難經(jīng)過較少的迭代被全部更新到,因此收斂速度略慢一些.
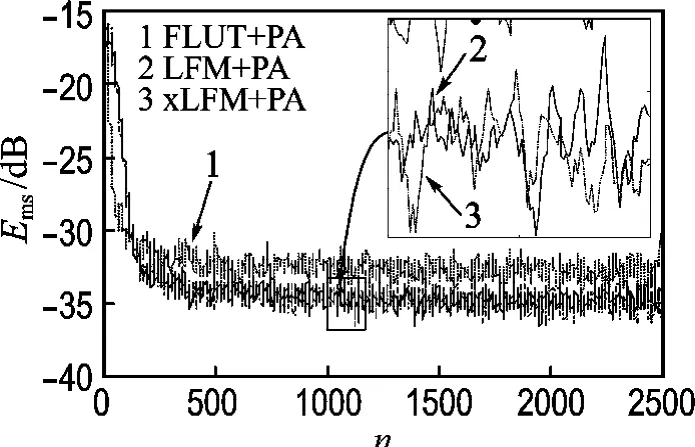
圖4 不同PD+PA系統(tǒng)的MSE曲線Fig.4 The MSE curves of different PD+PA systems
用于僅更新非線性系統(tǒng)的采樣點數(shù)目的多少對仿真結(jié)果也有影響.當(dāng)采樣點較少時,以100個采樣點為例,x LFM+PA和LFM+PA系統(tǒng)的MSE曲線如圖5所示.由圖5可以看出訓(xùn)練次數(shù)對x LFM的影響比較大,也就是說LFM對PA逆特性的跟蹤能力較x LFM的強.
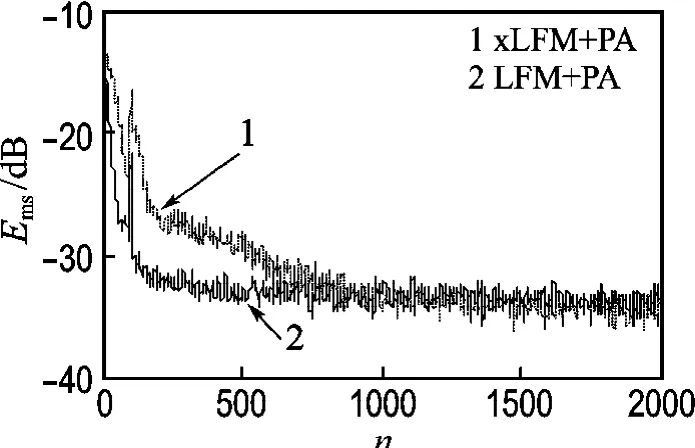
圖5 兩種PD+PA系統(tǒng)的MSE曲線Fig.5 The MSE curves of two kinds of PD+PA systems
圖6為下列信號的功率譜密度(PSD,Dps)曲線:(1)輸入信號;(2)只經(jīng)過功率放大器輸出的信號;(3)帶各種PD的PA輸出信號.從圖中可以看出,LFM對邊帶的壓縮效果最好,x LFM略次于LFM,但兩者都顯然優(yōu)于FLUT和傳統(tǒng)HPD.
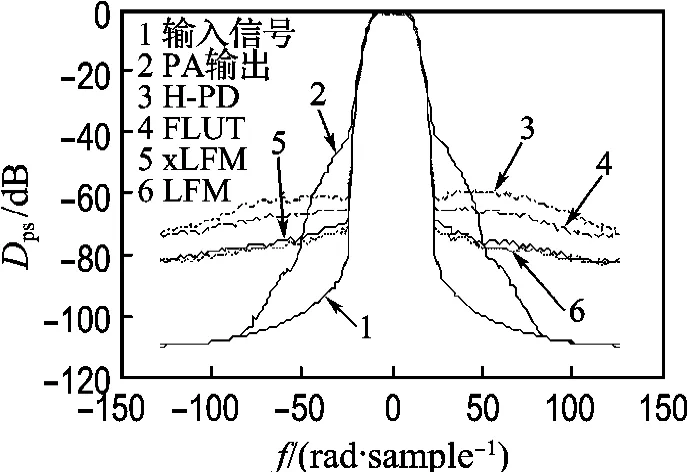
圖6 各系統(tǒng)的PSD曲線Fig.6 The PSD curves of different systems
表1給出了H-PD、FLUT和LFM(x LFM)模型復(fù)雜度以及每次迭代更新所需要計算參數(shù)個數(shù)的比較,其括號內(nèi)的數(shù)值是根據(jù)本文仿真實驗中各預(yù)失真器參數(shù)的具體取值得到的.由此表可以看出,本文提出的Hammerstein預(yù)失真器雖然減少了每次迭代所需更新的參數(shù)個數(shù),但卻增加了需要更新的表項個數(shù),較大地增加了模型參數(shù)個數(shù).因此,本文預(yù)失真器精度的提高是以增加模型的復(fù)雜度和存儲單元的個數(shù)為代價的.
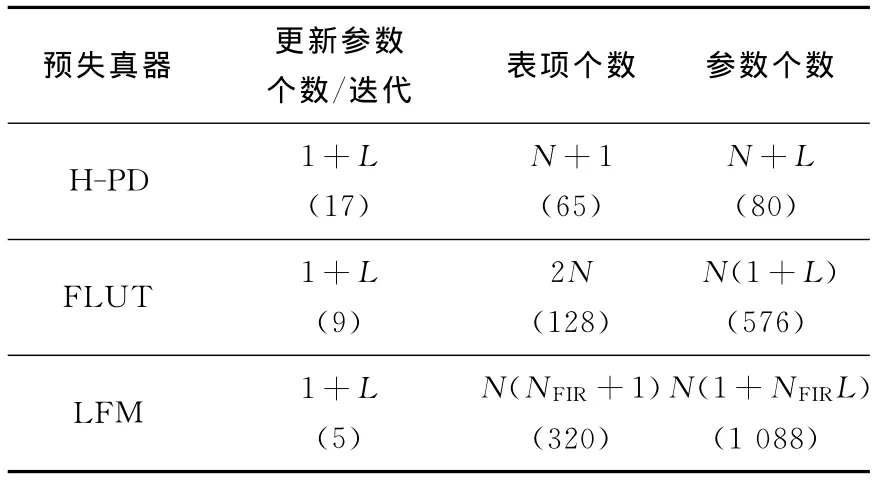
表1 各預(yù)失真器對比表Tab.1 The comparative table of different PDs
仿真實驗證明:對FLUT線性子系統(tǒng)的改進,使新得到的Hammerstein預(yù)失真器能夠有效地補償帶記憶效應(yīng)功率放大器的非線性失真.在系統(tǒng)要求不苛刻的情況下,可以采用本文提出的預(yù)失真器x LFM.
4 結(jié) 語
預(yù)失真器建模的精確度是直接影響對帶記憶效應(yīng)功率放大器非線性失真補償?shù)年P(guān)鍵因素之一,尤其是模型對功率放大器逆記憶特性的描述能力.本文提出的改進的Hammerstein預(yù)失真器以LUT級聯(lián)濾波器矩陣作為其實現(xiàn)形式,更精確地描述了PA的逆記憶效應(yīng)特性,提高了系統(tǒng)的整體性能.仿真實驗證明:本文提出的PD能更加有效地補償帶記憶效應(yīng)PA的非線性失真.在保證對PA線性化性能的前提下,提出較簡化的Hammerstein預(yù)失真器實現(xiàn)形式是今后研究的方向.
[1]HE Zhi-yong,GE Jian-h(huán)ua,GENG Shu-jian,etal.An improved look-up table predistortion technique for HPA with memory effects in OFDM systems[J].IEEE Transactions on Broadcasting,2006,52(1):87-91
[2]崔 華.基于BPNN的OFDM系統(tǒng)的HPA預(yù)失真[J].電子與信息學(xué)報,2009,31(6):1451-1454
[3]CHOI Sung-h(huán)o,JEONG Eui-rim,LEE Y H.Adaptive predistortion with direct learning based on piecewise linear approximation of amplifier nonlinearity[J].IEEE Transactions on Microwave Theory and Techniques,2009,57(5):1119-1128
[4]HAMMI O,GHANNOUCHI F M.Twin nonlinear tow-box models for power amplifiers and transmitters exhibiting memory effects with application to digital predistortion[J].IEEE Microwave and Wireless Components Letters,2009,19(8):530-532
[5]RAWAT M,RAWAT K,GHANNOUCHI F M.Adaptive digital predistortion of wireless power amplifiers/transmitters using dynamic real-valued focused time-delay line neural networks[J].IEEE Transactions on Microwave Theory and Techniques,2010,58(1):95-104
[6]DENNIS R M,MA Z,KIM J.A generalized memory polynomial model for digital predistortion of RF power amplifier[J].IEEE Transactions on Signal Processing,2006,54(10):3852-3860
[7]HAMMI O,GHANNOUCHI F M,VASSILAKIS B.A compact envelope-memory polynomial for RF transmitters modeling with application to baseband and RF-digital predistortion[J].IEEE Microwave and Wireless Components Letter,2008,18(5):359-361
[8]JARDIN P,BAUDOIN G.Filter lookup table method for power amplifier linearization[J].IEEE Transactions on Vehicular Technology,2007,56(3):1076-1087
[9]MKADEM F,BOUMAIZA S.Extended Hammerstein behavioral model using artificial neural networks[J].IEEE Transactions on Microwave Theory and Techniques,2009,57(4):745-751
[10]曹新容,黃聯(lián)芬,趙毅峰.一種基于Hammerstein模型的數(shù)字預(yù)失真算法[J].廈門大學(xué)學(xué)報(自然科學(xué)版),2009,48(1):47-50
[11]AI Bo,YANG Zhi-xing,PAN Chang-yong,etal.Analysis on LUT based predistortion method for HPA with memory[J].IEEE Transactions on Broadcasting,2007,53(1):127-131

