配網分布式電源并網對電網潮流的影響

陳永秋，羅振威，顧 全

（1.江門供電局，廣東 江門 529000；2.南京南瑞繼保電氣有限公司，南京 211100）

分布式發電（distributed generation，DG）通常是指發電功率在幾千瓦至數百兆瓦的小型模塊化、分散式、布置在用戶附近的、高效、可靠的發電單元，主要包括：以液體或氣體為燃料的內燃機、微型燃氣輪機、太陽能發電（光伏電池、光熱發電）、風力發電和生物質能發電等［1］。

分布式發電的優勢在于可以充分開發利用各種可用的分散存在的能源（包括本地方便獲取的化石類燃料和可再生能源），并提高能源的利用效率。分布式電源通常接入中壓或低壓配電系統，并會對配電系統產生廣泛而深遠的影響。

1 分布式電源潮流計算分析

傳統配電網中一般包含2種節點類型：Vθ節點和PQ節點，其中：V為電壓幅值；θ為相角；P為有功功率；Q為無功功率。變電站出口母線通常視為Vθ節點，其它節點（包括負荷節點和中間節點）都視為PQ節點。隨著各種分布式電源加入配電網絡，系統中出現了新的節點類型，主要包括：①P恒定、V恒定的PV節點；②P恒定、電流幅值I恒定的PI節點；③P恒定、V不定、Q受P和V限定的PQ（V）節點。在進行計算時，需要針對不同的節點類型采用不同的處理方法，其本質是在潮流計算的每個迭代步驟上將各種類型的節點轉換成為傳統方法能夠處理的PQ節點或 PV 節點［2，3］。

由于牛頓法具有二階收斂特性，在配電網潮流計算中仍然保持著收斂速度和迭代次數方面的優勢。雖然配電網末端母線電壓偏低，但正常運行情況下，各節點的電壓也在額定電壓附近，各節點的電壓相角差也不會很大，初值采用平啟動的方式，牛頓法都能得到滿意的結果。所以在配電網潮流計算的實際應用中，牛頓法仍然是一種性能優良的潮流計算方法［4，5］。具體潮流計算流程如圖1所示。

2 DG接入電網的性能評估

本文以IEEE-33節點母線測試系統為例，33節點配電系統如圖2所示（0為平衡節點），支路編號與該支路的受端節點編號一致。三相功率的基準值SB=10MVA，線電壓的基準值UB=12.66 kV，根節點電壓標幺值為1.0，計算精度ε=10-6。系統總有功負荷為3 715 kW，總無功負荷為2 300 kvar。

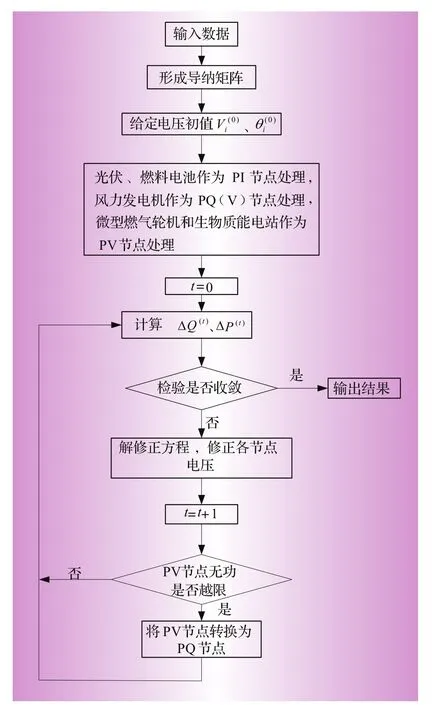
圖1 含DG的配電網牛頓法潮流計算原理

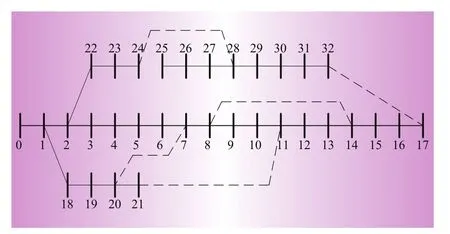
圖2 IEEE-33母線測試系統

33節點配電系統中接入的各種類型的DG參數如下：①光伏電站：有功功率150 kW，I*=0.016 6；②燃料電池電站：有功功率250 kW，I*=0.027 7；③風力發電機：有功功率1.5 MW，定子電抗Xs=0.036 92Ω，定子電阻Rs=0.001 692Ω，轉子電抗Xr=0.037 59Ω，轉子電阻Rr=0.002 423Ω，勵磁電抗Xm=1.456 8Ω，恒定功率因數0.89（滯后）；④微型燃氣輪機電站：有功功率150 kW，V*=0.98；⑤生物質能電站：有功功率2.5MW，V*=0.98。

2.1 光伏電站接入電網分析

以光伏電站接入電網后的潮流分析為例。假設在節點32處接入一臺光伏電站，新節點編號為33，按照上述潮流計算方法分析，潮流計算結果如表1所示（迭代4次），節點電壓曲線如圖3所示。

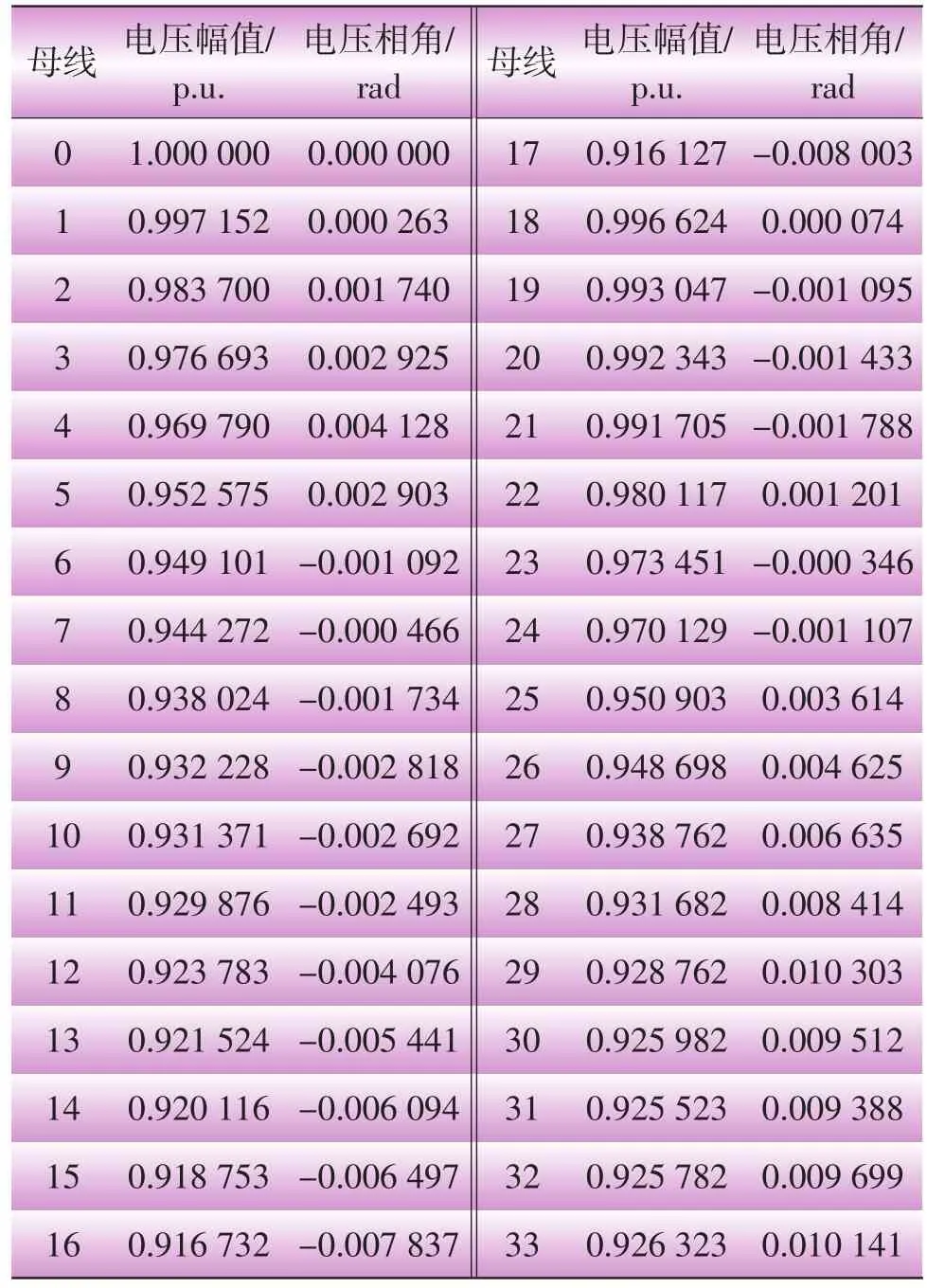
表1 單臺光伏電站接入潮流計算結果

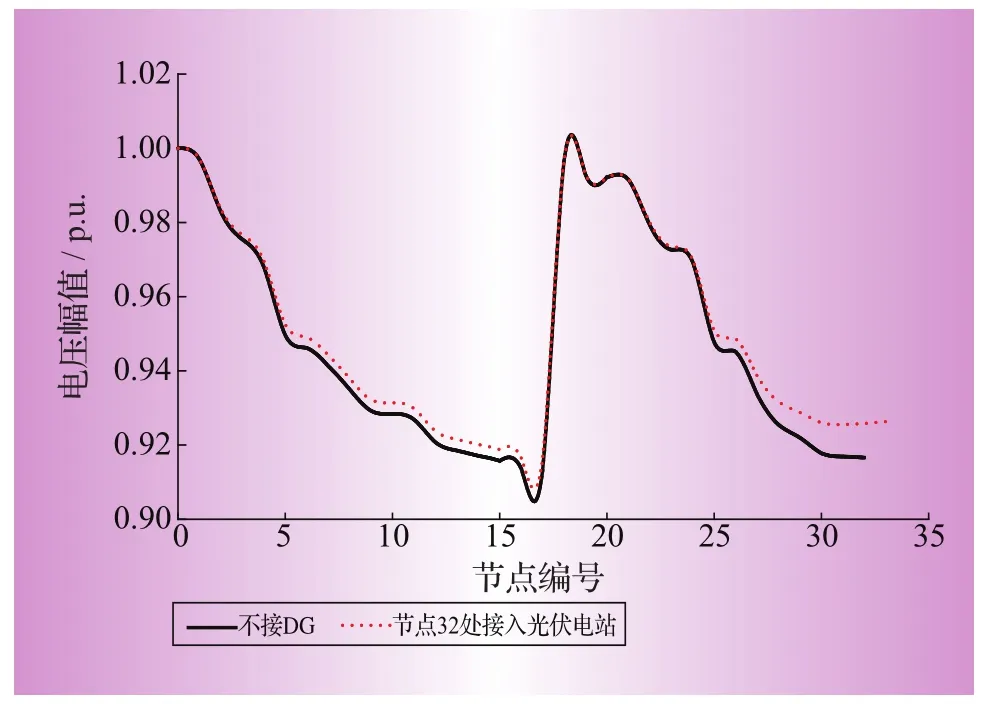
圖3 節點32接入DG后的節點電壓

同理，用上述方法分析在節點17處接入一臺光伏電站以及在節點32和節點17處分別接入一臺光伏電站之后對配電網潮流的影響，如圖4所示。

分析圖4可以發現，不論光伏電站是接在17號母線末端還是接在32號母線末端，系統各母線的電壓都有所提高。接在主饋線17號母線的末端，對于整個系統的電壓提升較高，均能達到0.92 p.u.以上；而接在分支饋線32號母線的末端，雖然能夠使得該條分支饋線的電壓提高得很多，但對于其他饋線（包括主饋線）的影響不是很大，對離電源點較遠的母線，電壓沒有得到明顯地提升。所以光伏電站接入配電系統，盡量在最長饋線的末端接入來改善系統電壓，因為該點是整個系統電壓降低最多的。

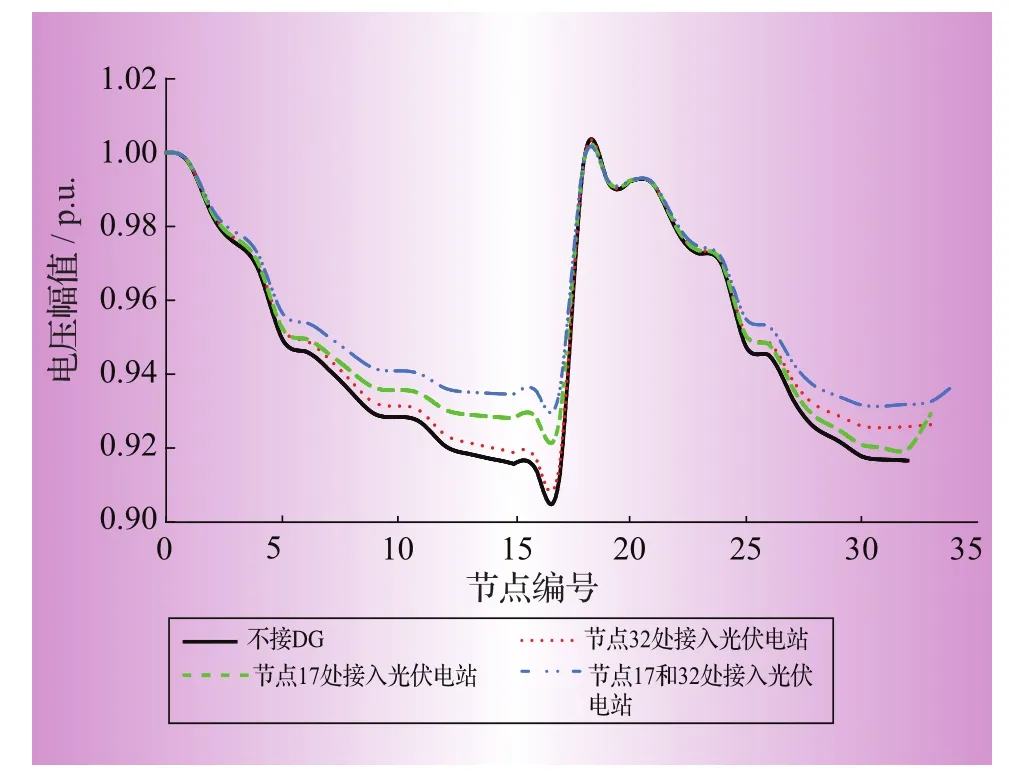
圖4 DG接入配電網的不同位置對潮流的影響

2.2 不同種類DG單獨接入電網對潮流的影響

不同種類的DG接在配電網同一母線處對系統電壓水平的影響如圖5和圖6所示。

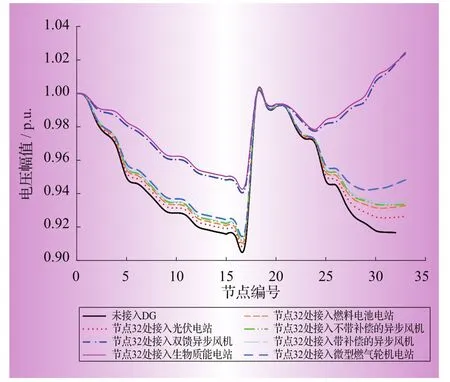
圖5 節點32接入不同DG后的節點電壓

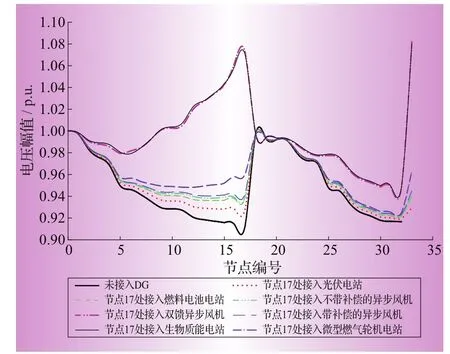
圖6 節點17接入不同DG后的節點電壓

燃料電池電站的接入對配電網潮流的影響，與光伏電站接入后的變化趨勢大致相同。因為在潮流計算中，它們同樣被視為PI節點進行處理，區別在于它們注入配電網的功率P及電流I不同，導致系統各點電壓提升的高低有所差異，注入功率大則電壓提升得高。

接入一臺600 kW的異步風機后，分別比較有補償電容器組和無補償的情況，系統各母線處電壓在有無功注入的情況下較沒有補償時提升得高一些，且對于風機所在的分支饋線影響較明顯，對于其它分支饋線的影響不大，即無功功率的就地補償。接在主饋線的末端時，整個系統電壓水平的提升較高。

雙饋異步風機的接入將接入處母線的電壓抬升得很高，同時使得該分支饋線的電壓也上升得很高。如果雙饋異步風機接入的位置不適宜，將會使某些母線的電壓越限，破壞系統的正常運行。在接入雙饋異步風機時，應該綜合考慮接入容量、接入位置等對于潮流的影響。

微型燃氣輪機接入系統是作為PV節點處理，能提供一定的無功功率，但當無功越限時將其轉化為PQ節點處理，適當將其電壓范圍放寬，相當于只做無功越限檢查而不做電壓越限檢查，以保證潮流收斂。這就是圖中看到的微型燃氣輪機接入點的電壓不等于PV節點規定的電壓值的原因，即微型燃氣輪機提供不了維持PV節點電壓恒定所需的無功功率，從而使得電壓有所下降。

接入的生物質能電站的容量為2.5MW，而系統總的有功負荷為3.715MW，因此相比其他形式的DG，生物質能電站的容量較大，同時又將其作為傳統的PV節點處理，使系統各母線電壓提升得非常厲害。比較接入母線17和母線32處2種情況可以看出，接入32號母線既能夠有效提升系統各母線的電壓，又保證了各母線電壓在安全運行范圍內。

2.3 多種DG接入電網對潮流的影響

在節點17處接入一臺光伏電站（編號33），節點32處接入一臺微燃機電站（編號34），節點21處接入一臺風機（編號35），節點24處接入一臺燃料電池電站（編號36），節點11處接入一臺生物質能電站（編號37），節點28處接入一臺帶補償的異步風機（編號38），得到的潮流計算結果（迭代5次）如表2所示，電壓水平曲線如圖7所示。

分析圖7可以發現：混接型系統的潮流計算能夠保證收斂，并且能使系統電壓都有所提高，但又不至于超過電壓限制，保證了系統的安全穩定。

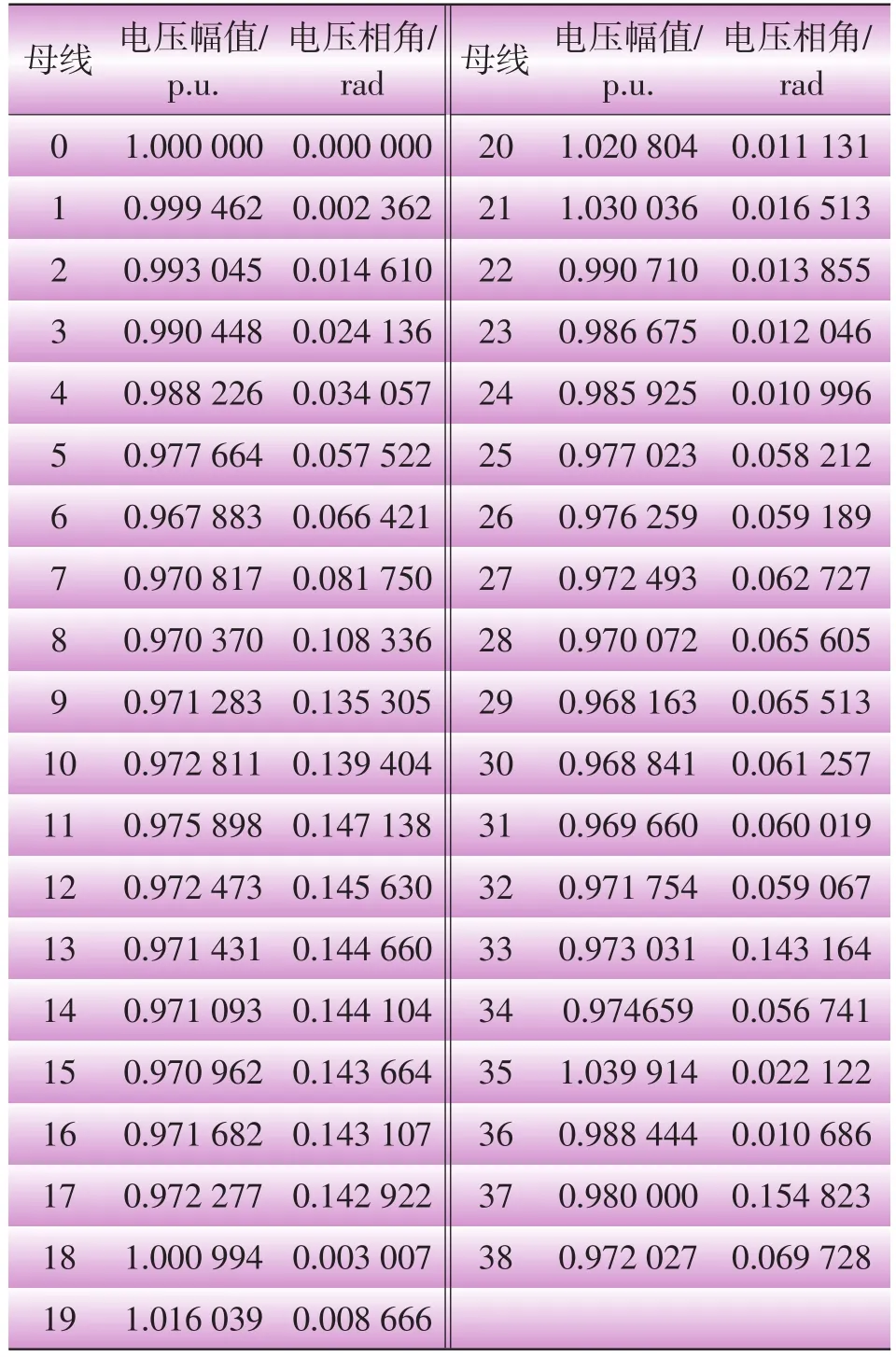
表2 混接型潮流計算結果

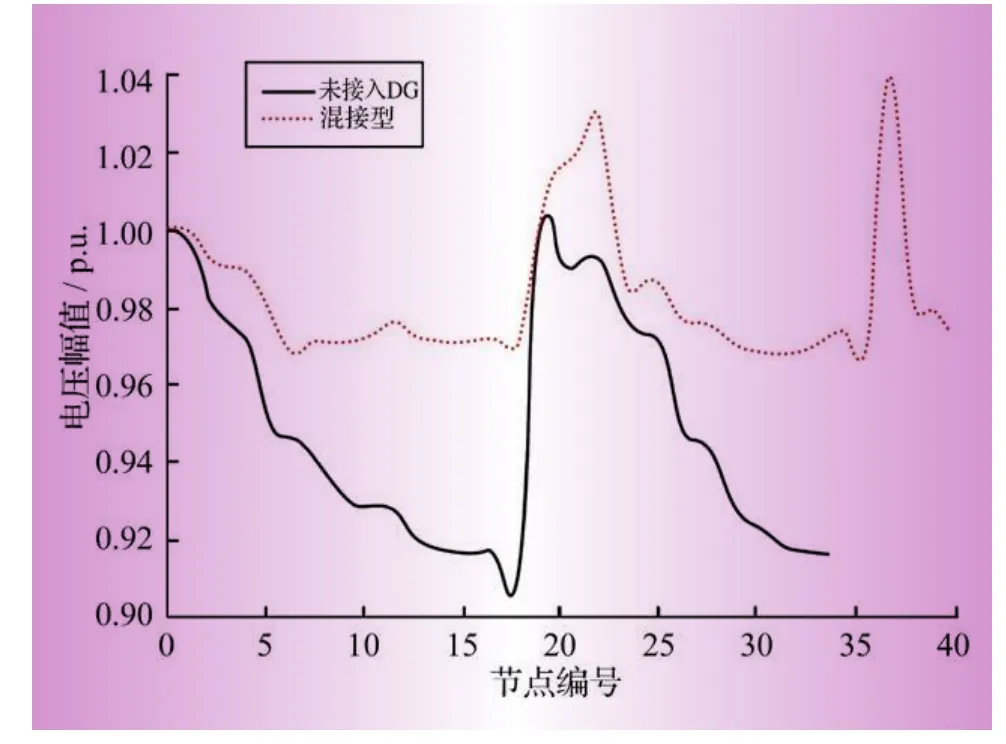
圖7 混接型系統各節點電壓

3 收斂特性分析

各種不同DG接入系統后，對算法收斂特性的影響如圖8所示，圖中縱坐標為功率誤差（節點電磁功率與節點負荷功率的差值）范圍，即收斂條件；橫坐標為迭代次數。從圖上可以看出，接入DG后迭代次數沒有明顯的增加，一般都能在迭代10次以內保證潮流收斂，表明牛頓法運用于含DG的配電網潮流計算是合適的。

PI型DG的接入對本算法的迭代次數影響不大，迭代次數基本不變。PQ（V）型DG，帶電容器組補償的異步風機（場）接入時，潮流迭代次數隨著精度的提高而增加，對應10-8精度的迭代次數增加了4次；帶變流器的雙饋風機（場）接入時，類似于PI型DG，隨著迭代精度的增加，迭代次數與無DG接入時的情況基本重合。PV型DG的接入對收斂性能有一定影響，在算例中最壞的情形是多迭代3次。多點混接的情況下，迭代次數相比無DG接入時最壞僅增加了3次。

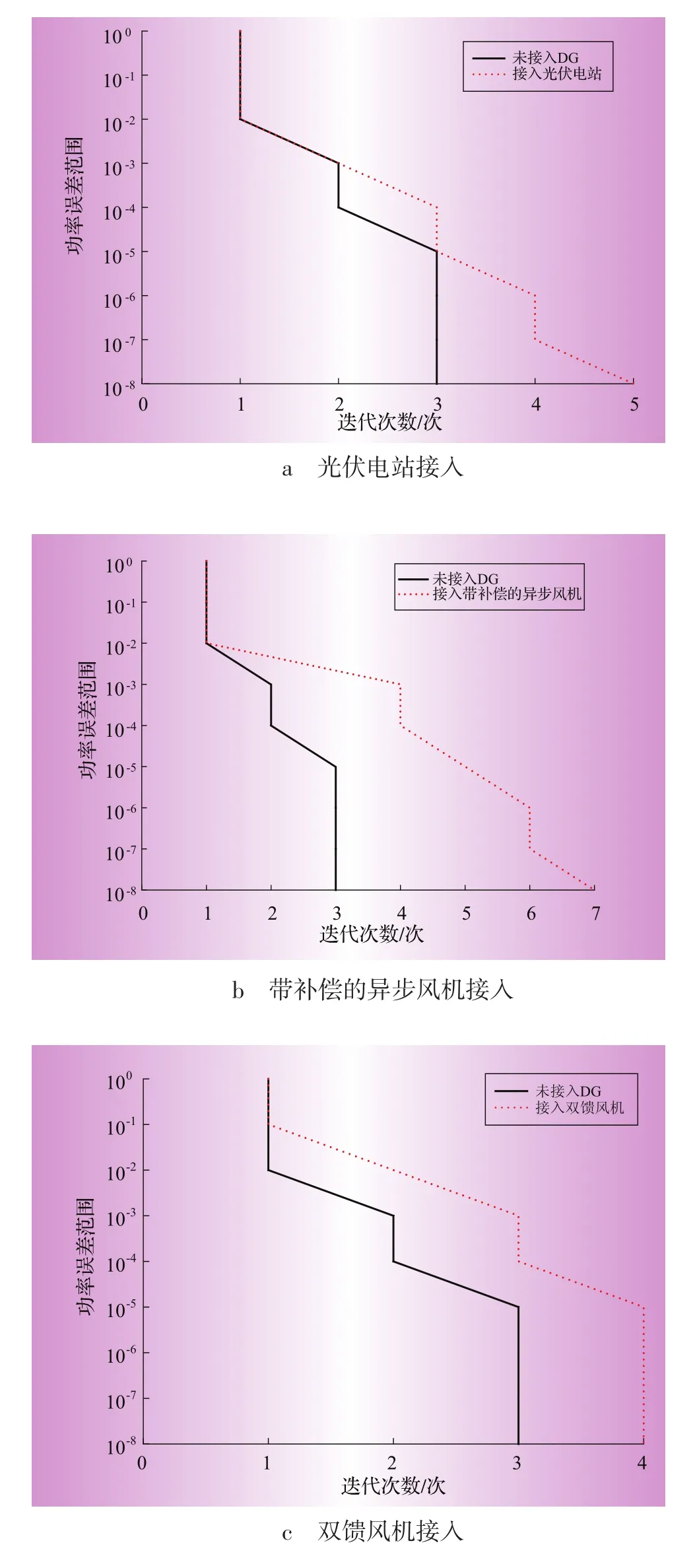
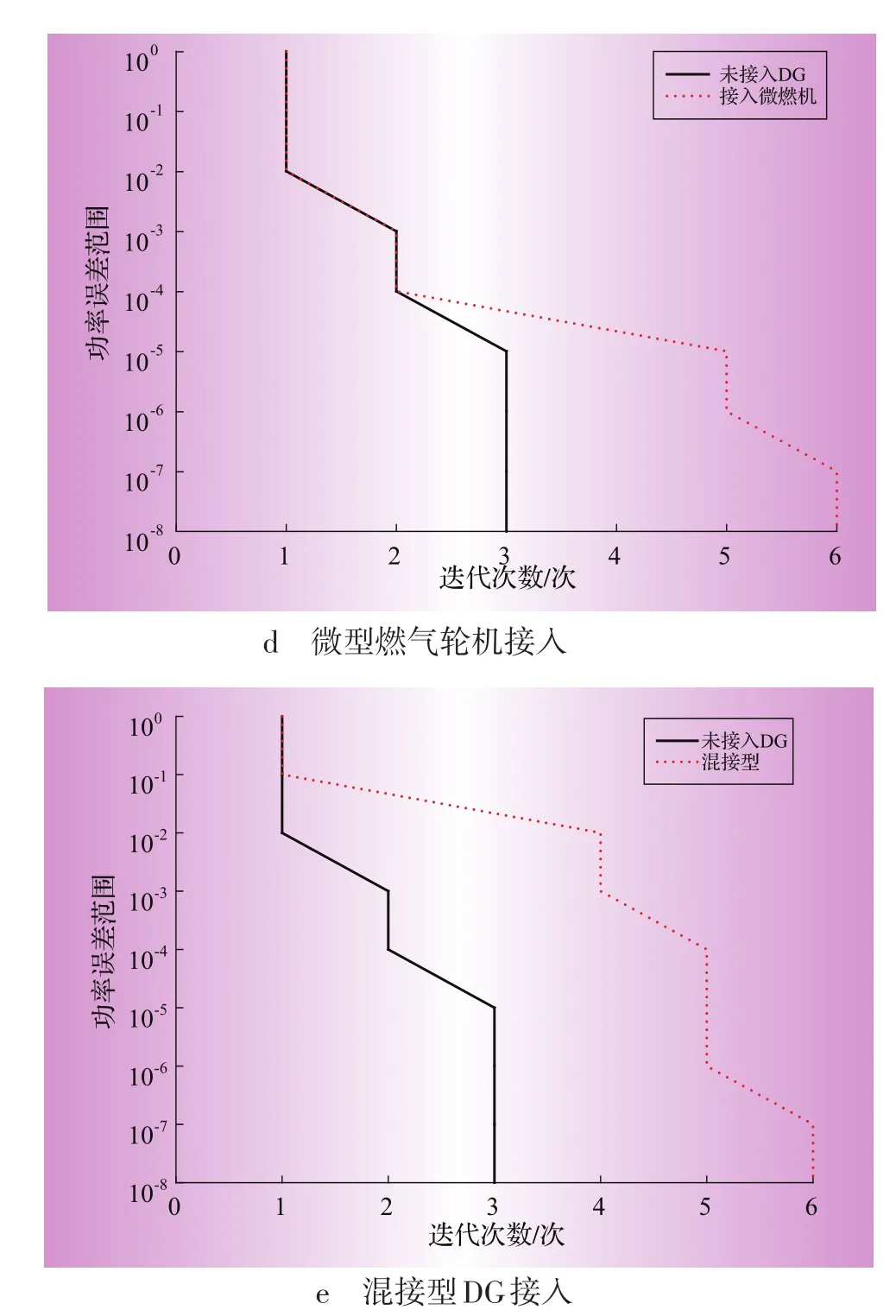
圖8 不同DG接入情況下的收斂特性

4 結論

綜合以上計算分析可以看出，基于牛頓法的含DG的配網潮流計算方法具有較快的收斂速度，針對各種復雜的DG類型和并網控制策略，其潮流計算結果能做到較好的收斂。

此外，DG的接入能有效抬升系統各節點電壓水平，尤其是具有無功輸出的DG，如：光伏電站（PI型）和微型燃氣輪機電站及生物質電廠（PV型）。

［1］ 殷桂梁，楊麗君，王珺.分布式發電技術［M］.北京：機械工業出版社，2008：11-19.

［2］ 陳海焱，陳金富，段獻忠.含分布式電源的配電網潮流計算［J］.電力系統自動化，2006，30（1）：35-40.

［3］ 鄭海峰.計及分布式發電的配電系統隨機潮流計算［D］.武漢：天津大學，2006.

［4］ 王志群，朱守真，周雙喜，等.分布式發電對配電網電壓分布的影響［J］.電力系統自動化，2004，28（16）：56-60.

［5］ 趙晉泉，江曉東，張伯明.潮流計算中PV-PQ節點轉換邏輯的研究［J］.中國電機工程學報，2005，25（1）：54-59.