基于子帶模式的AMC技術算法分析

于躍清，袁 華，肖秋根，夏 鳴

（空軍大連通信士官學校 指揮自動化系，大連 116600）

0 引言

在OFDM系統中，我們假設每個子載波內處于平坦衰落，但是對于不同的子載波，它們的信道狀況不盡相同。如果對所有子載波采用相同的調制編碼方案，那必然造成頻譜利用率的下降或者FER和BER的增大；但如果對每個子載波分別進行調制編碼方案的選擇，一方面會大大增加需要傳輸的信令信息量，造成頻譜資源的浪費，另一方面也會提高對硬件設備的要求，得不償失。因此我們將子載波進行分組，每個分組作為一個子帶（subband），每個子帶中的子載波采用相同的調制編碼方案，不同子帶獨立選擇調制編碼方案，事實上這是對上述兩種情況的折衷。

1 子載波分組

子載波分組可以分為動態分組和靜態分組兩種。動態分組是根據每次傳輸各個OFDM子載波的信道狀況，實時調整分組的大小和所包含的子載波。動態分組對子載波的分組相對精確，但這種方法要求同時傳輸每次分組的信息，如果不能保證分組信息量小于單獨子載波調制方式的信息量，那分組將失去意義。

靜態分組是根據系統的情況和具體通信環境以及通信質量的要求，在每次通信之前首先確定子載波的分組，并且每次傳輸都不改變分組方式，因此最多只需傳輸一次分組信息，對頻譜效率基本不產生影響。靜態分組參數主要有分組數和分組大小；分組數指的是將子載波分成的分組個數，即總共包含的子帶數；分組大小表示每個子帶所包含的子載波個數。本文選擇分組大小相等的靜態分組。

分組大小的選擇也是在實際當中應該考慮的問題。一般要求滿足：

其中BC為信道的相干帶寬， F為子載波帶寬，NS為一個分組中子載波數。

2 子帶模式的AMC系統中的算法

2.1 子帶信噪比選擇算法

與基于子載波的AMC系統不同，在基于子帶的AMC系統中，由于子載波進行了分組，要求每一個子帶采用一種調制編碼方案，子帶的信噪比的計算選擇就成為首要解決的問題。

2.1.1 極端值代替法

極端值代替法是指用子帶中質量最差或最好的子載波的信噪比作為子帶的信噪比，主要有以下兩種形式：

子帶中最差子載波代替：

子帶中最好子載波代替：

SNRk,i表示第k個子帶中第i個子載波的信噪比。

2.1.2 均值法

極端值代替法沒有體現子帶中所有子載波的狀況，雖然算法簡單，對設備要求低，但是整個系統的性能犧牲也會比較大，這里我們用簡單統計的方法考慮均值法。

均值法就是將信道估計得到的各個子載波的信噪比作平均，并用這個均值()作為子帶的信噪比來選擇下次傳輸所采用的調制方式，用樣本平均值表示為：其中NS表示子帶k中的子載波數。從統計學角度上看，可以用子帶子載波信噪比的均方差進行修正 ，其中我們用均值減去均方差作為子帶的信噪比。

2.2 子帶比特加載算法

基于子帶的系統模型如圖1所示，在整個帶寬內，分割成了NC個子載波，所有的子載波被分成NB個子帶。因此，每個子帶中的子載波數為Ncb=NC/NB。每個OFDM符號所承載的比特數為RTOT=，其中bave是系統的平均頻譜效率。優化準則為，當在固定傳輸功率的條件下保持目標傳輸速率時，降低誤碼概率。

分配到第i個子帶上的比特數為：

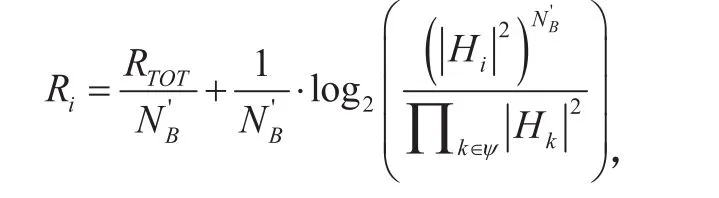
這樣就把所有RTOT個比特分配給NB個子帶。

其中Hi定義為子帶平均信道增益，是屬于那個子帶的Ncb個子載波的信道增益的平均值。，其中hk為第k個子載波的信道增益。 為在當前比特分配時，所包含的子帶數目的集合。 表示包含在 內的子載波數，初始情況下， 。

如果對于 ，Ri為非正數，相應的子帶必須在子帶集合 中排除，并且，比特分配要重新進行。直到在剩下的 個子帶中，所有的Ri都為正數，迭代才能終止。

此外，在實際當中，每個子載波的比特數必須為一個整數。因此，Ri被量化為：

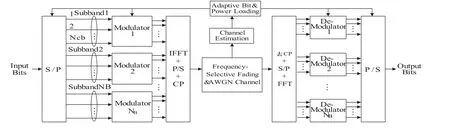
圖1 基于子帶模式的自適應OFDM系統框圖

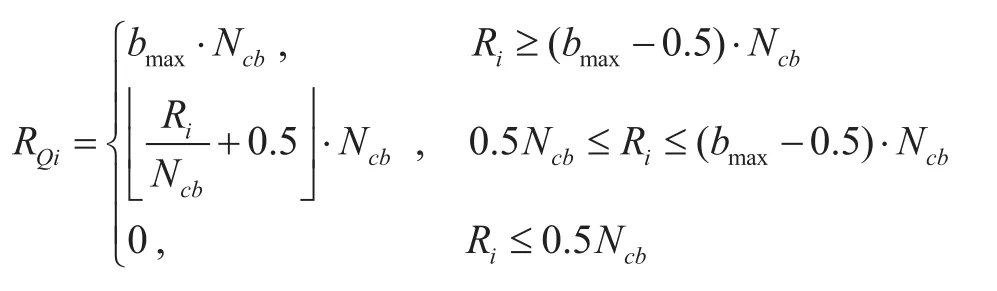
其中 為量化比特數，bmax為每一個子載波最大允許傳輸的比特數， 為小于x的最大整數。量化誤差為 。

3 子帶分組方法的改進

實際中子帶如何進行分組，依據怎樣的規則把所使用的子載波分成若干個子帶，假設所有NC個子載波依據頻率的高低按升序排列，第一個子載波占用最低的頻譜，第NC個子載波占用最高段的頻譜。

3.1 連續子帶分組法

這種方法是把所有NC個子載波按照順序簡單地分成NB個子帶，例如第i個子帶為。

3.2 分類子帶分組法

基于子帶模式的分組方法在降低系統性能增益的情況下希望能夠減少信令信息的傳輸。由于子帶的平均信道增益和屬于這個子帶的子載波的實際信道增益之間的差異，導致了系統性能的降低。為了減小這種差異，提出一種分類子帶分組的方法。在這種方法中，所有的子載波按照信道增益的升序排列。分類子載波的序列號設置為 ，各項滿足 。然后，所有NC個子載波根據序列號被分組成NB個子帶。例如第i個子帶中的子載波為從直觀上來看，這種分類子帶分組的方法能夠使子帶的平均信道增益和屬于這個子帶中的子載波的信道增益的差異減小。

從圖2可以看出，因為采用了分類的方法，使子帶的平均信道增益與每一個子載波的實際信道增益變小，所以分類子帶分組方法的性能要優于連續子帶分組方法的性能。仿真中采用的是Greedy比特分配算法，子載波個數為128。

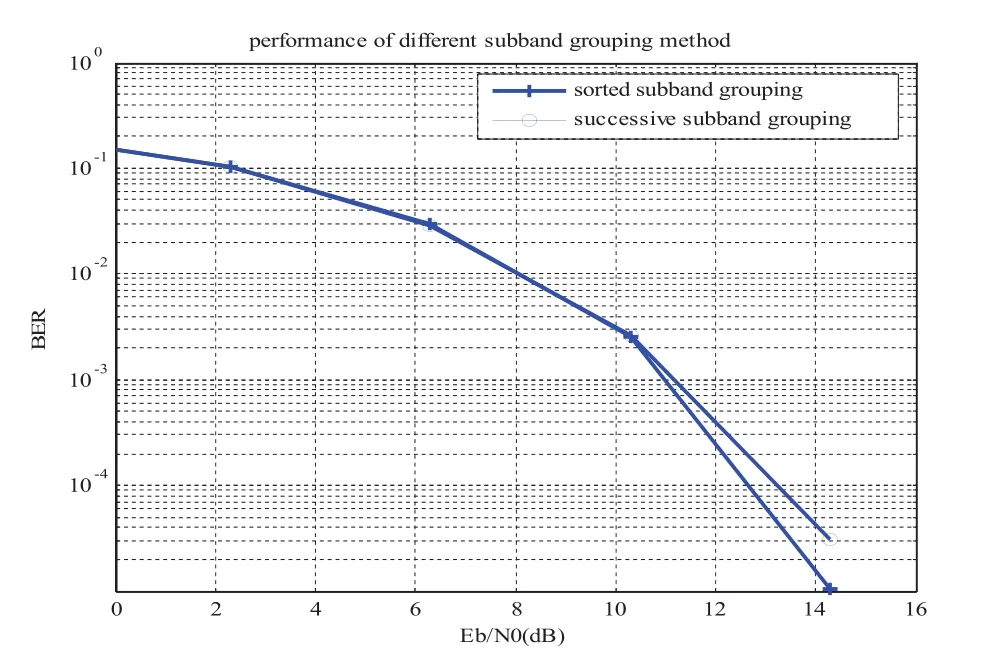
圖2 連續與分類子帶分組法的性能比較

[1] Andrea J Goldsmith, “Adaptive Coded Modulation for Fading Channels”, IEEE Trans Communications,1998,46:595-602.

[2] Ana Garc′ a-Armada, “SNR Gap Approximation for M-PSK-Based Bit Loading” IEEE Transactions on wireless communication,2006,5(1):57-60.