單繞組五相永磁無軸承電機的SVPWM 控制

姜海博 黃 進 康 敏

（1.浙江大學電氣工程學院 杭州 310027 2.浙江科技學院電氣學院 杭州 310013）

1 引言

無軸承電機是近20 年以來發展起來的一種新型懸浮電機。與傳統的磁懸浮電機相比，除了繼承了其無需潤滑、軸承無磨損的特點之外，無軸承電機把產生懸浮力的繞組疊繞在電機定子內部，使懸浮力繞組與電機的電樞繞組組成一個整體，從而不占用額外的軸向空間，克服了磁軸承電機臨界轉速低、轉矩小等不足[1-3]。

目前大多數的無軸承電機研究都采用雙繞組的結構形式，其技術也最成熟，其中一套繞組提供電磁轉矩，另一套繞組提供懸浮力[2-3]。

單繞組無軸承電機通過特定的控制算法和繞組連接方式，在一套繞組中同時通入轉矩電流和懸浮電流，破壞氣隙磁場的固有平衡，實現電機的平穩懸浮。相比于傳統雙繞組電機，其優勢主要體現在電機損耗的下降和電機加工難度的降低。目前單繞組無軸承電機的研究主要集中在裂相繞組、橋式和多相繞組三種單繞組結構[4-9]。本文采用的五相永磁無軸承電機在更改傳統五相電機繞組結構之后，利用多相電機的多自由度的特點實現了電機的穩定懸浮[8-9]。

電機的運行性能除了與其控制方法有關，還與其調制方式有關。相比于傳統的SPWM 控制方式，SVPWM 由于其較高的電壓利用率得到了廣泛而深入地研究[10-14]。在文獻[10]中，John W.Kelly 對九相SVPWM 進行了研究，并發現隨著相數的提高，雖然相比于傳統的SPWM 仍有優勢，但逆變器的電壓利用率提高的百分比隨著相數提高而下降。而在文獻[11]中，Hyung-Min Ryn 等人提出改變選取d3-q3 平面的電壓參考值可以進一步地提高電壓利用率，此方法可以應用于多相電機非正弦供電的場合。

本文針對多相單繞組無軸承電機自身的特點，在d1-q1 平面和d2-q2 平面選取了合適的電壓空間矢量，兼顧了電機的轉矩和懸浮性能，成功實現了電機的平穩懸浮。

2 五相無軸承電機的SVPWM 控制

對于一臺無軸承電機當且僅當電機中存在同頻且極對數相差為1 的兩個磁場時，可以產生穩定的懸浮力。通過對多相電機多控制自由度和磁動勢的分析，發現更改電機繞組結構之后在電機繞組中注入兩組相位差不同的電流（轉矩電流I1和懸浮電流I2）可以在一臺多相電機中的兩個平面內分別產生兩個極對數相差為1 的磁場[8-9]。

2.1 電壓矢量的選取

一臺五相電機具有兩個控制自由度。在五相集中整距繞組電機中，繞組具有基波和三次空間諧波，可通過注入三次諧波電流來改善磁場，提高轉矩密度[14]。而在五相單繞組無軸承電機中，由于產生可控懸浮力的需要，各相繞組不再含有三次空間諧波分量（或者這一分量很小），主要含有基波和二次空間諧波，所以可分別注入轉矩電流I1和懸浮電流I2以產生轉矩和懸浮力[9]。由于I2和三次諧波電流在存在相位差上的不同，為便于分析，可將原五相正交變換矩陣中d3-q3 平面改寫為d2-q2 平面，這兩個平面上的電壓空間矢量的分布有所不同（兩個平面合成空間矢量旋轉方向相反）。下文分析如何在d1-q1 平面和d2-q2 平面選取合適的空間矢量以實現電機的平穩懸浮。

電機的定子五相繞組在空間上是對稱的，互差72°分布。對于此五相電機，可以分別在d1-q1 平面和d2-q2 平面定義兩組電壓空間矢量

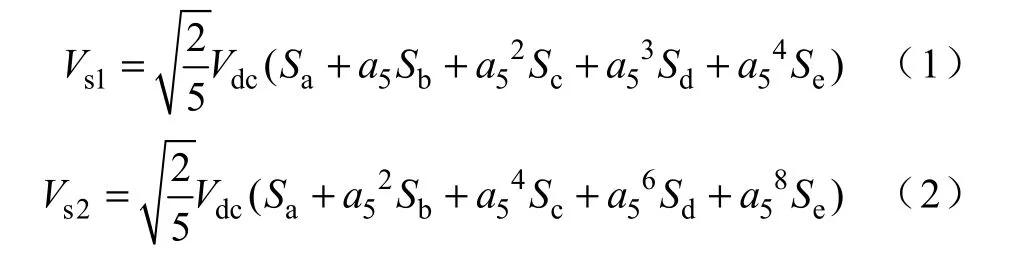
式中，a5=ej2π/5；Vdc為直流母線電壓；S 表示電機各相的開關狀態；其中1 表示上橋臂導通，若其為0，則表示下橋臂導通。

對于一臺五相電機，共有25=32 個電壓矢量，其中兩個零矢量。由式（1）和式（2）可以求得逆變器各個開關狀態的電壓矢量在 d1-q1 平面和d2-q2 平面電壓矢量的分布，如圖1 和圖2 所示。

圖1 d1-q1 平面電壓矢量圖 Fig.1 The voltage vectors on d1-q1 plane

圖2 d2-q2 平面電壓矢量圖 Fig.2 The voltage vectors on d2-q2 plane

兩個平面內的電壓空間矢量按照幅值可以分為大矢量，中矢量和小矢量。令U1，U2，U3分別表示大矢量、中矢量和小矢量的幅值，由式（1）、式（2）可以求得

如圖1 和圖2 所示，d1-q1 平面內的大矢量，映射到d2-q2 平面后均為內環的小矢量，為了取得較好的轉矩控制性能，選取了d1-q1 平面的外環和中環四個矢量進行電壓合成。比如在1 區間內，就會選取電壓矢量（10000），（11000），（11001），（11101）4 個電壓矢量，t1，t2，t3，t4分別代表了這4 個電壓矢量的作用時間，根據伏秒平衡原理，可以得到[11]

式中，t0表示零矢量作用時間。

參考圖2，對應懸浮平面與轉矩平面電壓矢量的相位關系，可以得到此時d2-q2 平面的電壓矢量。

2.2 扇區的判斷

[15]中判斷三相電機扇區的方法，將其應用到一臺五相電機中。可以采用下述方法對扇區進行判斷。

首先引入B0，B1，B2，B3，B4，令

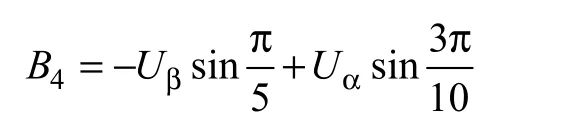
再令

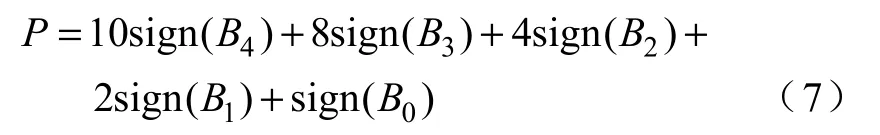
式中，sign(x)是符號函數，如果x＞0，sign(x)=1，如果x＜0，sign(x)=0。

圖3 為簡單的扇區圖，當扇區為粗線下方的扇區（1，7，8，9，10）時，sign(B1)=1，反之sign(B1)=0。由式（7）求出P 值之后，根據P 值查下表，即可確定當時采樣周期內的扇區號。

圖3 五相電機空間矢量的扇區分布 Fig.3 The sector allocation for 5 phase SVPWM

表 扇區真值表 Tab. Truth table

2.3 電壓矢量應用時間的計算

由式（4）和式（6）可以建立起第一扇區內兩個平面的電壓和電壓矢量的作用時間（t1,t2,t3,t4）之間的關系，同理可以把結論推廣到第n 個扇區，轉換矩陣如式（9）所示[11]。

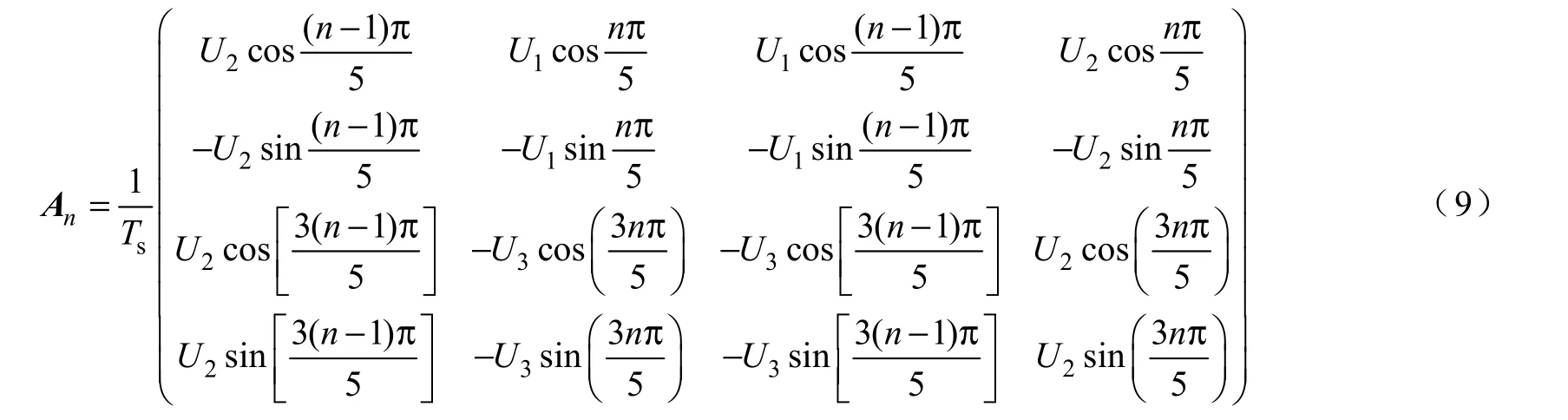
因為矩陣An是可逆的，所以矢量的作用時間和零矢量作用時間t0可由下式求出

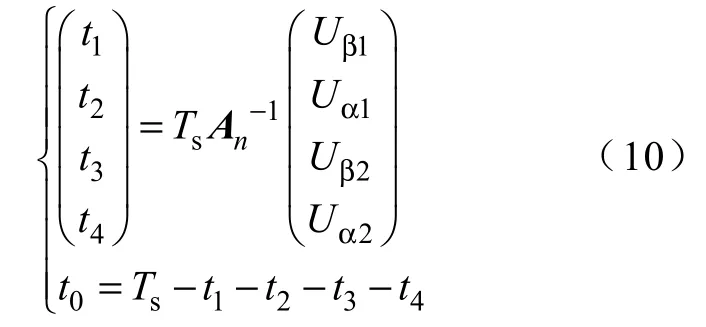
在實驗中發現若采用式（10）對t1,t2,t3,t4進行求解會占用大量的系統資源，極大地降低控制效率，所以應分別對10 個扇區進行求解，每個扇區對應的變換矩陣為常值矩陣。而且可以注意到在互為對角的兩個扇區內合成兩個幅值相等，相位相反的電壓矢量時，同一時間同一相上下橋臂兩功率管導通關系互補。換言之，即對于n＞5 的扇區，變換矩陣可以寫為

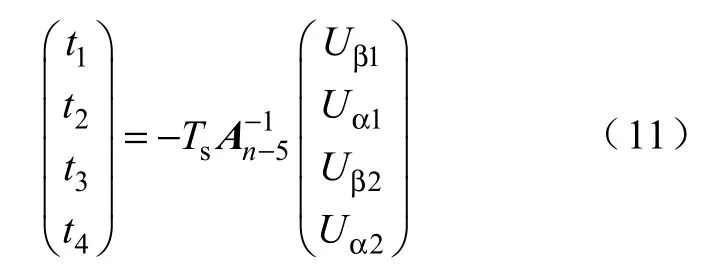
這樣通過扇區矩陣的內在聯系，減少了計算量，大大節省了程序所占空間。通過以上分析，由式（10）、式（11）可以畫出每個扇區功率管的驅動信號圖，圖4 為扇區1 各相的驅動信號。

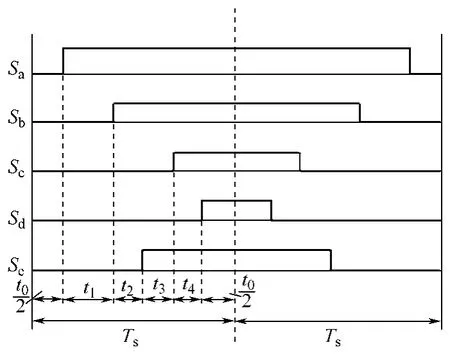
圖4 各相功率元件在扇區1 內的導通時間 Fig.4 The conducting time for each power device on sector 1

將各個扇區內計算出的各相的導通時間寫入相應的比較寄存器，即可完成整個SVPWM 算法。

3 控制系統與實驗結果

本系統控制框圖如圖5 所示，無軸承電機的運行性能可以分為兩個方面：轉矩性能和懸浮性能，由兩個不同的平面（d1-q1，d2-q2）分別控制。對于轉矩平面，采用id=0 矢量控制，通過光電碼盤讀取電機速度信號，經過速度調節環可以求得轉矩電流的給定值。對于懸浮平面，首先采用兩個正交的電渦流位置傳感器經過A/D 采樣，測出位置信號實際值，經過PID 調節器可以分別求得α 和β 方向的懸浮力參考值，進而可以通過式（12）求得懸浮電流的給定值[9]。

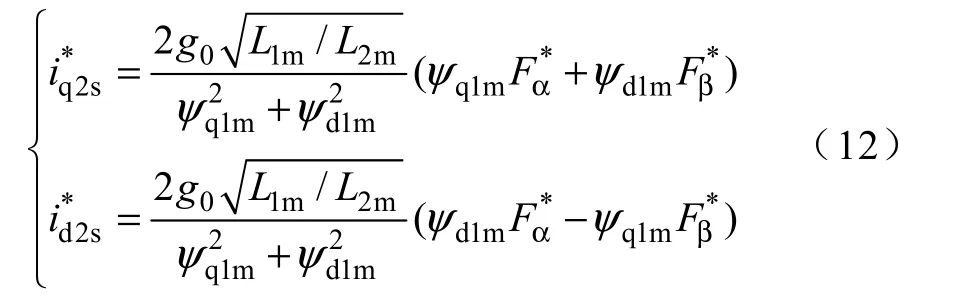
式中

其中，L1m，L2m分別表示d1-q1 平面和d2-q2 平面的等效電感；g0表示氣隙長度。

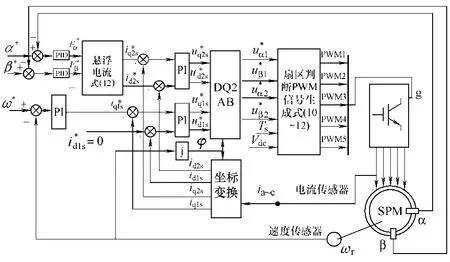
圖5 電機的控制系統框圖 Fig.5 The control diagram of the system

通過d1-q1 平面電流閉環，可以求得d1-q1 平 面內需要跟蹤的電壓矢量；同理d2-q2 平面 內的電流閉環可以求得d2-q2 平面內需要跟蹤的電 壓矢量。可以按照本文所述的SVPWM 算法 選取電壓空間矢量，進而得到各相功率元件的驅動信號。

由以上分析可知，對多相單繞組無軸承電機，其d2-q2 平面的電壓矢量是由懸浮力閉環產生的，與 d1-q1 平面的電壓矢量并不存在確定的相位關系，而是與對應時刻轉子所需的懸浮力方向有關；此外d2-q2 平面電壓矢量的幅值由轉子所需的懸浮力的幅值決定。

實驗樣機參數：Rs=1.51Ω，L1m=0.0372H，L2m=0.0073H，L0s1=L0r1=0.0012H，L0s2=L0r2=0.001H，m=10kg，J=0.011kg·m2，氣隙長度g0=2mm，永磁體寬度3mm，設計時引入機械輔助軸承將軸限制在±0.33mm 的范圍內防止定轉子直接接觸。

圖6 為采用日本YOKOGAWA 公司生產的16通道波形記錄分析儀（型號DL750）測得的SVPWM控制策略的實驗結果，從上至下分別表示電機的轉速，電機的轉矩電流，懸浮電流和電機β，α方向的位移（?α方向為電機重力的方向）。

圖6 實驗波形 Fig.6 Experimental result waveforms

在圖6 中，0～0.5s 是電機定位到d 軸之后的波形，此時電機并未加懸浮力，所以電機轉子停留在外加支撐的輔助軸承上；0.5s 時突加懸浮力，電機轉子被迅速拉到中心位置附近，當t=0.5～2s 時，電機處于靜態懸浮狀態，此時轉速保持為0，轉矩平面電流也為0，但懸浮平面已經存在懸浮電流來為系統提供懸浮力。

在電機的靜態懸浮過程中，由于位置環選取了較大的積分參數，電機實際上會以一個很低的頻率沿轉子中心作微小的振蕩，電機在1.6s 之前實際仍處于調制過程中，α方向的轉子位移并沒有位于電機中心；而在1.6s 之后電機更接近轉子中心。

當t=2～3s 時，電機處于加速過程，從0 加速到1500r/min；當t＞3s 時，電機以1500r/min 的速度旋轉。實驗結果表明電機在加速過程中和穩定旋轉時均可穩定懸浮，電機的徑向位移可以被控制在80μm 之內。

4 結論

區別于傳統多相電機利用諧波平面電壓矢量來實現改善磁場，提高功率密度以及提高電壓利用率等控制目標，本文利用多相電機多控制自由度的概念，在d1-q1 平面和d2-q2 平面內分別實時控制跟蹤給定的電壓空間矢量，同時保證了電機的穩定旋轉和平穩懸浮。實驗結果證明單繞組五相永磁型無軸承電機采用此控制算法可以有效而穩定地運行。

參考文獻

[1] Chiba A,Deido T,Fukao T,et al.An analysis of bearingless AC motors[J].IEEE Trans.on Energy Conversion,1994,9(1):61-68.

[2] 王寶國,王鳳翔.磁懸浮無軸承電機懸浮力繞組勵磁及控制方式分析[J].中國電機工程學報,2002,22(5):105-108.

Wang Baoguo,Wang Fengxiang.Excitation and control analysis of levitation force winding for magnetic suspension bearingless motors[J].Proceedings of the CSEE,2002,22(5):105-108.

[3] 朱熀秋,沈玉祥,張騰超,等.無軸承異步電機數學模型與解耦控制[J].電機與控制學報,2007,11(4):321-325.

Zhu Huangqiu,Shen Yuxiang,Zhang Tengchao,et al.Mathematicsmodel and decoupling control for self-bearing induction motors[J].Electric Machines and Control,2007,11(4):321-325.

[4] Bartholet M T,Nussbaumer T,Silber S,et al.Comparative evaluation of polyphase bearingless slice motors for fluid-handling applications[J].IEEE Transactions on Industry Application,2009,45(5):1821-1830.

[5] Khoo W K S.Bridge configured winding for polyphase self-bearing machines[J].IEEE Transa- ctions on Magnetics,2005,41(4):1289-1295.

[6] Ribeiro R L A,Castro F E F,Salazar A O,et al.A suitable current control strategy for split-phase bearingless three-phase induction machine[C].IEEE 36th Conference on Power Electronics Specialists,2005:701-706.

[7] 朱俊,鄧智泉,王曉琳,等.單繞組無軸承永磁薄片電機的原理和實現[J].中國電機工程學報,2008,28(33):68-74.

Zhu Jun,Deng Zhiquan,Wang Xiaolin,et al.Principle and implementation of the single winding bearingless permanent magnetic slice motor[J].Proceedings of the CSEE,2008,28(33):68-74.

[8] Huang J,Kang M,Yang J Q.Analysis of a new 5-phase bearingless induction motor[J].Journal of Zhejiang University Science A,2007,8(3):1311- 1319.

[9] Jiang Haibo,Huang Jin,Kang Min.Principle and realization of a 5-phase PM bearingless motor drive[C].6th International Power Electronics and Motion Control Conference,Wuhan,China,2009:1852-1857.

[10] Kelly J W,Strangas E G,Miller J M.Multiphase space vector pulse width modulation[J].IEEE Transactions on Energy Conversion,2003,18(2):259- 264.

[11] Ryu H M,Kim J H,Sul S K.Analysis of multi-phase space vector pulse width modulation based on multiple d-q spaces concept[C].IPEMC 2004,Xi’an,China,2004,3:1618-1624.

[12] Grandi G,Serra G,Tani A.Space vector modulation of a nine-phase voltage source inverter[C].ISIE,2007:431-436.

[13] 薛山,溫旭輝.一種新穎的多相 SVPWM[J].電工技術學報,2006,21(2):68-72.

Xue Shan,Wen Xuhui.Novel multiphase SVPWM[J].Transactions of China Electrotechnical Society,2006,21(2):68-72.

[14] Xue Shan,Wen Xuhui,Feng Zhao.Multiphase permanent magnet motor drive system based on a novel multiphase SVPWM[C].IPEMC,2006,1:1-5.

[15] 陸海峰,翟文龍,張磊.基于調制函數的 SVPWM算法[J].電工技術學報,2008,23(2):37-43.

Lu Haifeng,Zhai Wenlong,Zhang Lei.SVPWM algorithm based on modulation functions[J].Transactions of China Electrotechnical Society,2008,23(2):37-43.