導氣式自動武器變質量熱力學計算模型研究

冉景祿，徐誠，趙彥峻

(南京理工大學 機械工程學院，江蘇 南京210094)

導氣式自動武器是指利用從槍管導氣孔流出的高溫高壓火藥燃氣推動自動機完成自動動作的武器，火藥氣體的恰當利用是自動武器良好動力學性能的基礎［1］。因此，研究導氣裝置的動力特性對于利用火藥燃氣和獲得自動武器良好的動力學特性都具有十分重要的意義。國外研究導氣式自動武器的動力學特性時，大多采用的布拉文經驗法、馬蒙托夫經驗法、布拉貢拉沃夫方法。國內的研究工作主要集中在2 個方面: 1)引進國外經驗模型［2］，并在此基礎上建立導氣裝置數值計算模型［2-3］。數值計算模型求解的參數較多，計算相對準確，經驗模型可求解的參數較少，誤差相對較大。2)模型的改進與應用，這些研究針對特定對象對文獻［1 -3］建立的計算模型進行部分改進，將其應用于側裝藥金屬風暴武器系統內彈道性能一致性問題［4］、導氣裝置優化設計問題［5-6］。但通觀所有參考文獻，可以發現:建立的數值計算模型和經驗模型都沒有考慮內彈道與導氣裝置耦合的變質量熱力學過程，而且模型存在方程多、參數多、誤差較大等不足; 所有的應用研究針對不同的研究對象改進模型時，也沒有將內彈道和導氣裝置通過火藥燃氣耦合起來考慮。所以，為了克服這些研究的不足，探索導氣式自動武器性能準確預測和結構參數的確定的方法，通過分析槍管和導氣裝置之間存在的變質量熱力學過程，建立了一個內彈道和導氣裝置耦合的導氣式自動武器變質量熱力學計算模型，該模型更客觀真實地描述了導氣式自動武器發射過程中的變質量熱力學過程，而且具有參數少、誤差小等優點，實例證明了該模型的正確性和可靠性。

1 導氣式自動武器變質量熱力學模型

1.1 物理過程及基本假設

導氣式自動武器的導氣裝置典型結構如圖1所示。當底火被擊錘撞擊后，發射藥開始燃燒，藥室壓力迅速增大，當彈丸底部壓力大于擠進壓力時，彈丸開始切入膛線加速運動。隨著火藥的燃燒和彈后空間不斷增大，彈丸底部的壓力逐漸減小，當彈丸位移大于導氣孔的開孔距離時，火藥燃氣自導氣孔流入導氣室，由于剛開始膛內壓力比導氣室壓力大很多，導氣孔處出現正向臨界(音速)流，隨著流入導氣室火藥燃氣的增多，導氣室壓力不斷增大，導氣孔處出現非臨界(音速)流。隨著彈丸繼續向前運動、活塞向后運動，當導氣室火藥燃氣作用于活塞斷面的力與復進簧的簧力相等時，活塞運動速度達到最大，這時膛內壓力會進一步減小，當膛內壓力小于導氣室壓力且其比值不超過某一特定值時，導氣室的高溫高壓氣體開始流入膛內，導氣孔處出現反向非臨界(音速)流，當膛內壓力與導氣室壓力的比值超過某一特定值時，導氣孔處出現反向臨界(音速)流。當彈頭后端面飛離槍口時，彈丸運動進入后效期，高溫高壓的火藥燃氣以極高的速度噴出，由于火藥燃氣的流速極快，壓力較大，彈丸仍然在受到火藥燃氣壓力的情況下加速運動，隨著彈丸位移的增加，火藥燃氣速度逐漸減緩，壓力逐漸減小，后效期結束，彈丸速度達到最大。

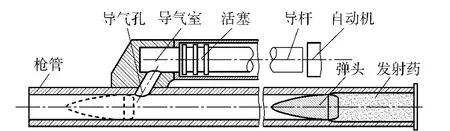
圖1 導氣裝置結構示意圖Fig.1 Sketch of gas-operated device

基本假設:

1)內彈道過程采用修正的經典內彈道模型描述;

2)導氣裝置內流場是一個有流入與流出的變質量熱力學過程;

3)由于是瞬態計算，忽略火藥燃氣與槍管和導氣室之間的熱量交換;

4)內彈道與導氣裝置通過火藥燃氣流量相互耦合。

1.2 計算模型

導氣式自動武器變質量熱力學計算模型包括內彈道模型、導氣室模型和耦合方程，具體形式如下:

膛內壓力變化方程

式中:pp、S、lψ、l、f、ω、Ik、Z、k、v、Gb、μk0、pk、ρk、L、n、ψ分別為導氣室壓力、槍管截面積、藥室長度、彈頭運動位移、火藥力、裝藥量、火藥燃氣的壓力全沖量、火藥已燃相對厚度、絕熱指數、彈頭運動速度、導氣孔處火藥燃氣的流量、槍口流量系數、槍口燃氣壓力、槍口燃氣密度、槍管長、多變指數、火藥已燃百分數。A、C 是與多變指數有關的常數。χ、λ、μ 為火藥的形狀特征量。

正比燃燒速度方程［7］

幾何燃燒定律方程［7］

彈頭運動位移方程［7］

彈頭運動速度方程［7］

式中:φ 為次要功系數; m 為彈丸質量。

從導氣孔流出槍管氣體質量方程

式中:η 為流出槍管氣體質量。

藥室自由容積縮徑表達式［7］

式中: W0為藥室初始容積; δ 為火藥密度; α 為余容。

槍管內火藥燃氣密度方程

式中:ρp為槍管內火藥燃氣密度。

氣室內氣體壓力變化方程［2］

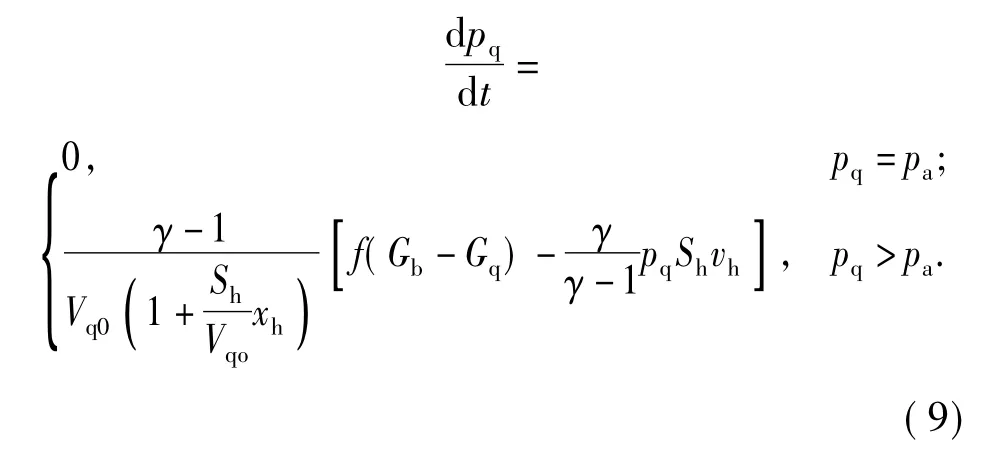
式中:pq、γ、Vq、Vq0、Sh、vh、pa分別為導氣室壓力、比熱比、導氣室容積、導氣室初始容積、活塞橫斷面面積、活塞運動速度、大氣壓強。

活塞間隙的流量方程［2］

式中:Gq、ΔSh、μq、γ、uq分別為活塞間隙氣體流量、導氣活塞的間隙面積、導氣室的流量系數、比熱比、氣體單位質量內能，K0為與γ 有關的常數。

氣室內氣體質量變化速度方程［2］

式中:mq為導氣室內火藥燃氣質量。

活塞運動方程

式中:K、xh、B、mh分別為緩沖簧剛度、活塞位移、隨動機構摩擦力和傳動阻力、活塞質量;F=(Pq-Pa)·Sh-Kxh-B 為活塞所受到的合力。

活塞運動位移方程［2］

氣室內氣流質量守恒方程

式中:ρq、lk分別為氣室內氣體密度和開孔距離。

氣室內單位質量氣體的比內能方程［2］

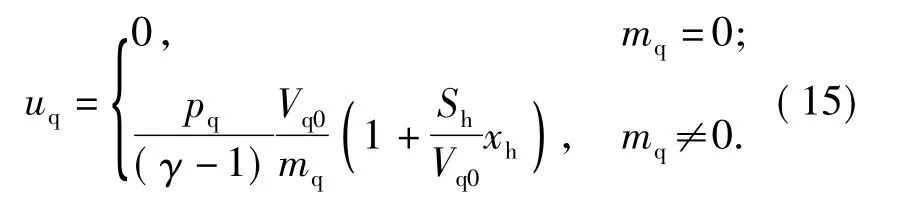
耦合(導氣孔流量)方程［1-2］

槍管內的內彈道過程與導氣裝置通過流量方程耦合在一起。

式中:μb、Sb分別為導氣孔處流量系數、導氣孔開孔面積;

2 模型驗證及計算結果分析

2.1 模型驗證

圖2為實驗獲得的某自動武器自動機速度時間圖，為了驗證所建模型的正確性，利用模型對某自動武器的各動力學參數進行數值計算。利用四階龍格庫塔法進行模型求解，采用MATLAB 編程實現。通過理論計算，得到某自動武器自動機的后坐初始階段速度時間圖，將其與實驗獲得的速度時間圖的后坐初始階段的曲線進行對比，如圖3所示。可以看出，由于沒有考慮發射時后坐力通過彈底對自動機速度的影響，理論計算時該段速度為0.當導氣室內火藥燃氣推動導氣活塞使自動機向后運動時，理論計算的速度曲線與實驗獲得的速度曲線吻合比較好，后坐的最大速度基本一致。從而表明本文建立的導氣式自動武器變質量熱力學計算模型是正確可靠的。

圖2 自動機速度時間圖Fig.2 v-t graph of automatic mechanism

圖3 后坐初始階段速度對比圖Fig.3 v-t at recoiled phase

2.2 計算結果分析

2.2.1 導氣孔處流量分析

某導氣式自動武器導氣孔處流量如圖4所示，當彈丸到達導氣孔時，膛內壓力很大，而導氣室內壓力僅為一個大氣壓，從而在導氣孔處出現正向臨界流，流量在瞬間達到1.16 kg/s;隨后流量開始下降，當彈丸飛離槍口，火藥燃氣快速噴出，膛內壓力迅速下降，導氣孔處燃氣出現正向非臨界流;當彈丸繼續向前運動，膛內壓力進一步下降，當導氣室壓力大于膛內壓力，導氣孔處出現反向非臨界流，最大反向非臨界流流量為0.18 kg/s;隨著導氣室內燃氣不斷流入膛內，導氣室壓力逐漸下降，流量隨之減小，直至為0.

圖4 氣體流量圖Fig.4 Gas flux

2.2.2 耦合量對膛壓、初速的影響

比較有無考慮耦合能量的膛內壓力曲線(如圖5所示)可以看出，在彈丸運行至導氣孔處到后效期段，膛內壓力曲線在開始和末端差別較小，而中間壓力之差相對較大的特點。其中，當彈丸剛飛離槍口端面時壓力之差達到最大的6.7 MPa.圖6為有無考慮耦合能量時彈丸的速度曲線，可以看出，火藥燃氣的耦合能量對彈丸飛行速度影響也較為明顯，對出膛速度的影響大約為6 m/s，在后效期的終了段，對速度的影響可達到最大的16 m/s.從而表明: 導氣孔流入導氣室的火藥燃氣對膛內壓力和彈丸初速有一定的影響，所以在內彈道求解和導氣裝置動力學求解時，應考慮從導氣孔流出的耦合能量對膛內壓力和初速的影響。

圖5 耦合能量對膛壓影響圖Fig.5 Impact of coupling energy on bore pressure

2.2.3 初始容積對導氣裝置影響

圖6 耦合能量對彈丸速度影響圖Fig.6 Impact of coupling energy on bullet speed

不同初始容積對導氣室壓力和自動機最大后坐速度的影響，如圖7、圖8所示。某自動武器導氣室的初始容積為1.7 ×10-6m3，此時，理論計算導氣室的最大壓力為23.7 MPa，自動機的后坐最大速度為8.61 m/s;當初始容積分別為2.2 ×10-6m3、2.7 ×10-6m3時，導氣室最大壓力分別為21.4、19.7 MPa，自動機的后坐最大速度分別為8.38、8.24 m/s.由此可以看出，隨著初始容積增大，導氣室壓力會減小，而且壓力峰值出現時間會后移，自動機后坐最大速度會減小，而且，隨著初始容積的增加，壓力減小的加速度會降低。這說明初始容積對導氣室的壓力、最大壓力出現的時間和自動機后坐的最大速度都有影響。換言之，在進行導氣裝置設計時可以通過調節導氣室的初始容積來調整導氣室內氣體的壓力及其出現的時間和自動機后坐的速度。

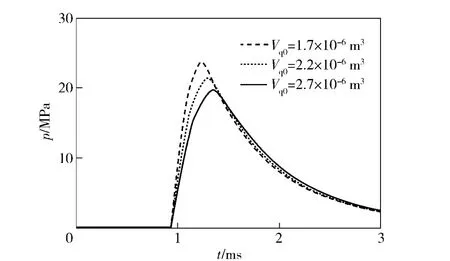
圖7 初始容積對導氣室壓力影響圖Fig.7 Impact of initial volume on gas chamber pressure

2.2.4 間隙對導氣裝置影響

不同間隙對導氣室壓力和自動機后坐速度的影響，如圖9、圖10所示。某自動武器導氣活塞與導氣筒的間隙為0.1 mm，此時，導氣室的最大壓力為23.7 MPa，自動機后坐最大速度8.61 m/s;當導氣活塞與導氣筒的間隙分別為0.5、1 mm 時，導氣室最大壓力分別為23.2、21.4 MPa，自動機后坐最大速度分別為8.48、8.18 m/s;這說明間隙在0.5 mm 以下變化，對導氣室壓力和自動機后坐最大速度影響不大。但當間隙增大到1 mm 時，導氣室的壓力較之0.5 mm 時減小了1.8 MPa，自動機后坐最大速度減小了0.3 m/s.說明間隙在0.5～1 mm 之間變化時，導氣室壓力和自動機后坐最大速度變化較為明顯。但壓力峰值到來的時間基本保持不變，這說明進行導氣裝置設計時導氣活塞與導氣筒的間隙控制在0.1～0.5 mm 之間比較合適。

圖8 初始容積對自動機速度影響圖Fig.8 Impact of initial volume on automatic mechanism speed

圖9 間隙對導氣室壓力影響圖Fig.9 Impact of clearance on gas chamber pressure

圖10 間隙對自動機速度影響圖Fig.10 Impact of clearance on automatic mechanism speed

2.2.5 導氣孔直徑對導氣裝置影響

不同導氣孔直徑對導氣室壓力和自動機后坐速度的影響，如圖11、圖12所示。隨著導氣孔直徑增大，導氣室壓力會隨之增大，自動機后坐速度也會隨之增大。而且開孔直徑在越小的值附近變化時，導氣室壓力和自動機最大后坐速度的變化越敏感。

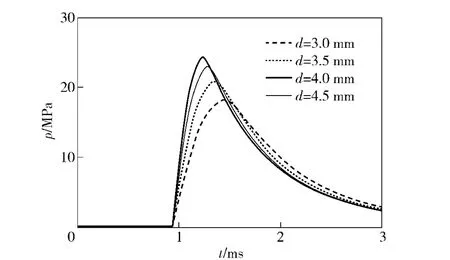
圖11 導氣孔對導氣室壓力影響圖Fig.11 Impact of clearance on gas chamber pressure

圖12 導氣孔對自動機速度影響圖Fig.12 Impact of clearance on automatic mechanism speed

3 結論

1)通過分析導氣式自動武器發射過程中身(槍)管和導氣裝置之間存在的變質量熱力學過程，建立了一個包括內彈道與導氣裝置耦合的一體化變質量熱力學模型，并以自動武器為實例驗證了該模型的正確性。

2)利用該模型求解了考慮耦合能量和不考慮耦合能量情況下，膛內壓力和彈頭速度的變化趨勢，得出耦合能量對兩者有一定影響，在進行內彈道和導氣室動力學特性精確求解時應該考慮該因素的結論。

3)本文建立的模型可以定量求解導氣裝置不同結構參數對導氣室壓力和自動機速度的變化，可用于探討各參數變化對導氣室壓力和自動機速度的影響規律。

4)本文建立的模型可以定量分析導氣式自動武器導氣孔處氣體流量變化，得出氣孔處氣體流量的基本變化規律。

References)

［1］甘高才.自動武器動力學［M］.北京: 兵器工業出版社，1990:26 -33.GAN Gao-cai.Dynamics of automatic weapon［M］.Beijing: The Publishing House of Ordnance Industry，1990: 26-33.(in Chinese)

［2］陸家鵬.自動武器學氣體動力學分冊［M］.北京: 國防工業出版社，1988:456 -464.LU Jia-peng.Gas dynamics of automatic weapon［M］.Beijing:The Publishing House of Ordnance Industry，1988:456 -464.(in Chinese)

［3］廖振強，王濤，余世海.武器氣體動力學數值計算方法［M］.北京:國防工業出版社，1988:221 -228 LIAO Zhen-qiang，WANG Tao，YUE Shi-hai.The calculation method of gas dynamics of weapon［M］.Beijing: The Publishing House of Ordnance Industry，1988:221 -228.(in Chinese)

［4］倪志軍，周克棟，赫雷.側裝藥金屬風暴武器系統內彈道性能一致性研究［J］.兵工學報，2005，26(5):595 -599.NI Zhi-jun，ZHOU Ke-dong，HE Lei.Consistency research of interior ballistic performances of the metal storm weapon system with side powder chambers［J］.Acta Armamentarii，2005，26(5):595-599.(in Chinese)

［5］韓曉明，薄玉成，王惠源，等.內能源轉管武器導氣裝置結構參數優化設計［J］.火炮發射與控制學報，2008，(2): 50 -53.HAN Xiao-ming，BO Yu-cheng，WANG Hui-yuan，et al.Optimal design of gas-operated device structure parameter in internallypowered gatling weapon system［J］.Journal of Gun Launch ＆Control，2008，(2): 50 -53.(in Chinese)

［6］王萬清.M60 式7.62 mm 通用機槍動力學分析及優化［D］.南京:南京理工大學，2007:21 -24.WANG Wan-qing.Analysis on dynamics and optimization of model M60 general purpose machine gun of the 7.62 mm caliber［D］.Nanjing: Nanjing University of Science and Technology，2007:21-24.(in Chinese)

［7］步兵自動武器及彈藥設計手冊編寫組.彈道及彈藥射擊: (上冊)［M］.北京:國防工業出版社，1977:39 -84.Compile Group of Infantry Automatic Weapon and Design of Ammunition.Manual of infantry automatic weapon and design of ammunition［M］.Beijing: National Defense Industry Press，1977:39-84.(in Chinese)