單領航者相對位移測量的多自主水下航行器協同導航

李聞白，劉明雍，張立川，劉富檣

(西北工業大學 航海學院，陜西 西安710072)

0 引言

隨著人工智能理論、傳感器技術和微計算機技術等的不斷成熟和發展，具有感知、思維和動作能力的自主水下航行器(AUV)在軍事和民用領域得到了廣泛的應用，如水下情報搜集、遠程水下攻擊、深海資源勘測和海底光纜鋪設等。就當前的技術而言，水下導航問題仍然是發展AUV 所面臨的主要挑戰之一［1］。導航系統必須提供遠距離及長時間范圍內的精確定位、速度及姿態信息，受AUV 自身的體積、質量、能源的限制及水介質的特殊性、隱蔽性等因素的影響，實現AUV 的精確導航是一項艱巨的任務［2］。

長基線(LBL)、短基線(SBL)和超短基線(USBL)系統作為三種傳統的水下導航方法，已被廣泛應用于潛艇和AUV 的實時導航與定位。這些系統的定位精度較高，但其中的一系列不足之處也是明顯存在的［3-4］。以常用的LBL 為例，布放、標定和回收水下傳感器基陣需耗費大量的時間、人力和物力，使用成本較高;此外，針對AUV 執行任務區域的不同，上述布放和回收工作需重復進行，制約了AUV 的活動范圍。SBL 和USBL 需要母船支持，減少了AUV 的靈活性和隱蔽性。

出于以上考慮，研究人員提出了利用多個AUV間的相互合作實現協同定位的導航方法［5］。它使得導航信息能夠分享，且擺脫了基陣(母船)的束縛，使用區域靈活，成本較低。通常多AUV 的協同導航采用主從式(Leader-Follower)，主AUV(領航者，Leader)裝備有高精度的導航通訊設備(如GPS、磁羅盤、多普勒速度儀、深度計、水聽器等)，從AUV(跟隨者，Follower)配備的傳感器精度相對較低。利用AUV 間的水聲通訊，可以測量出各個不同時刻主、從AUV 間的相對位置信息，AUV 在各采樣周期內的相對位移由自身的航位推算獲得。根據上述信息并結合AUV 的運動學方程，利用擴展的Kalman濾波(EKF)方法就可以求取各從AUV 在不同時刻的定位估計。

為將系統復雜度及對量測手段的要求減到最小程度，人們提出了用一個領航者，僅利用距離信息的協同導航方法［6］。Bahr［7］等研究了單領航者AUV的協同導航，給出了基于極小化代價函數的CN 導航算法(CN-Algorithm)，但該算法對代價函數中Kullback-Leibler 距離(KL divergence)的求解過于復雜，沒有考慮定位解算的實時性。Gadre［8］等通過單AUV 領航者與單固定信標相結合的導航方法來提高定位精度，給出了基于EKF 的協同導航算法，但固定信標的引入制約了AUV 的活動范圍，同時減少了隱蔽性。Baccou［9］等采用領航者、跟隨者AUV 間的適當機動來解決單個距離信息求解不充分的問題，通過設定初始化機動路徑，利用Levenberg-Marquardt 方法(LM-Algorithm)優化協同導航EKF 算法中的濾波初值，并以此提高定位精度。但是，LM優化算法的收斂性與自身迭代初值的選取密切相關，不適當的初值往往導致其收斂到錯誤結果，因此在實施過程中至少需要選取50 組以上的不同初值進行迭代試驗，利用統計方法篩選出最終的正確結果，這將使得算法的復雜性大為增加，從而降低導航算法的實時性與穩定性。

本文針對上述研究中存在的問題，結合單領航者AUV 協同導航系統的定位原理和運動學模型，基于相對位移測量、航位推算信息及相鄰時刻主、從AUV 間相對位置的幾何關系，提出了一種多AUV協同導航算法。該算法的原理直觀、簡捷，具有較高的定位精度，同時兼顧了導航解算的實時性要求。仿真結果驗證了該算法的可行性和有效性。

1 數學模型

主、從AUV 均配備有各自的導航系統，其中包括磁羅盤、多普勒速度儀和水聽器等傳感器。如圖1所示，tABk時刻AUV A、AUV B 間的距離為rAB(tABk)，其中k 表示A、B 間的第k 次數據傳輸;A、表示tAkB時刻AUV A 的推位B 間的航位推算信息在tAkB時刻實現交換，pADR(tAkB)=導航位置坐標，由A 的航位推算系統獲得。

理論分析可知，由(1)式可以確定AUV B 的位置坐標(xB1，yB1)，而依次累加ΔpB12，ΔpB23…即可求得后續時刻AUV B 的位置坐標更新。進一步，方程組(1)存在唯一解的必要條件是向量組［xA1，yA1］T，和［x3A+Δx1B3，y3A+Δy1B3］T線性獨立。也就是說，AUV A 和AUV B 不能以相同的速度沿同一方向平行航行，否則協同導航問題將無法求解(此時協同導航系統全局不可觀測)，這與已有的研究結果是吻合的［8］。

在實際應用中，利用代數方法或數值算法通過(1)式直接求解(xB1，yB1)是不被采用的，這將導致(xB1，yB1)敏感地依賴于系統的輸入(當系統近似不可觀測時尤為顯著)從而失去意義。因此，設計適當的EKF 導航算法是可行途徑，在下一節中具體展開討論。

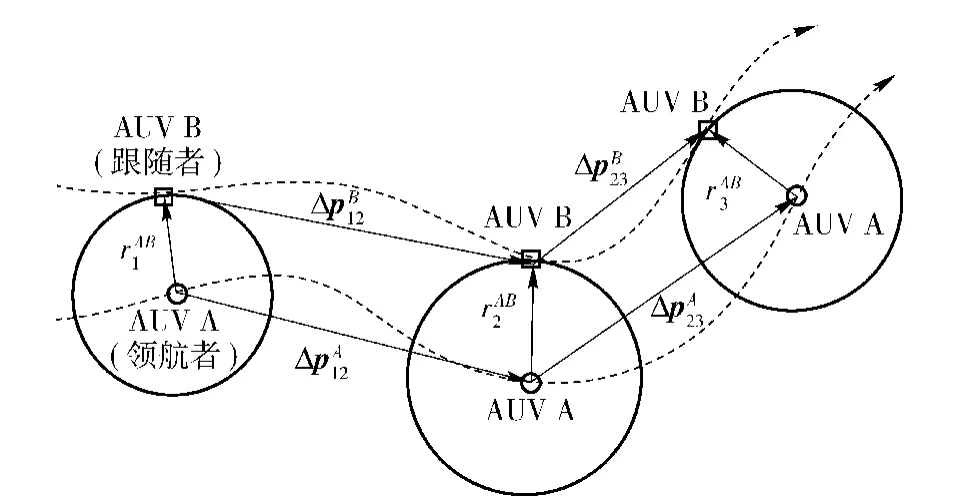
圖1 主從式多AUV 協同導航系統Fig.1 Leader-Follower cooperative navigation system of multiple AUVs

2 協同導航算法

2.1 狀態估計

記pAB=pB-pA表示AUV A、AUV B 間的相對位置，其一階導數為=vAB，設pABlc表示主、從AUV在時刻的最新一次相對位置數據傳輸，則協同導航系統的狀態方程可以寫為

式中，ηv是具有零均值的高斯白噪聲，var ηv=diag設系統的狀態更新時間為Ttu，則與(2)式相對應的離散時間狀態方程為(“-”表示先驗估計)

式中，系統噪聲

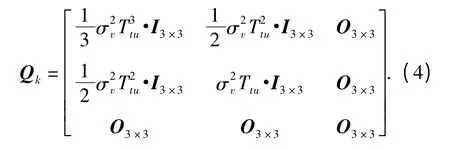
2.2 量測方程與方差更新

主AUV A 可近似連續地獲得自身的航位推算定位信息，并經由水聲通訊周期性地獲取從AUV B的航位推算位置。由于漂移誤差的存在，上述航位推算結果的定位誤差將隨時間的推移持續增長，其增長特性服從高斯白噪聲過程［10］

利用連續相鄰時刻主、從AUV 的相對位移信息，可以建立系統的位移差量測方程

結合誤差模型(5)可得(6)式的量測誤差分布

相應的位移差量測矩陣為

位移差量測噪聲矩陣為

此外，主、從AUV 間的相對速度量測矩陣為

速度量測噪聲矩陣為

式中，σ2hz，σ2vt分別表示水平與垂直方向的測速誤差。

下面討論濾波方差的更新。由于狀態向量中已經包含了主、從AUV 在tABk時刻的最新一次相對位置數據傳輸pABlc，因此結合位移差量測方程的構造形式可知，此時濾波方差的更新過程具有比經典的EKF 算法中更為簡潔的形式。設Pk(-)表示k 時刻濾波方差的先驗估計，ΔpABk為k 時刻新獲得的位移差量測值，則濾波方差的更新可以分為兩步(“+”表示后驗估計):

其中方括號部分表示與Pk(+)中相對應的子矩陣。

2.3 量測數據的選取

考慮到水下通訊環境的復雜性，在相對位置量測數據被用于濾波之前，應舍棄部分錯誤的量測值以確保Kalman 濾波器具有較快的收斂性。為此，可以利用先驗方差矩陣Pk(-)來判斷tABk時刻所獲得的pAB(tABk)是否為一“好”的量測值。Pk(-)的主對角項描述了狀態變量估計誤差的方差。對于狀態向量s(tABk)=［(pAB(tABk))T(vAB(tABk))T主對角線的前兩項分別是主、從AUV 的相對位置坐標ΔxAkB，ΔyAkB估計誤差的方差σ2Δx(tAkB)，σ2Δy(tAkB).由此，可以定義一個描述時刻相對位置估計不確定性的圓域，其半徑為

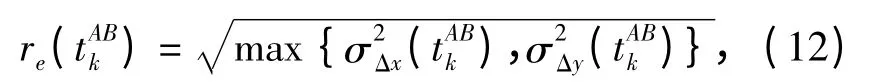
此時，如果量測值pAB(tABk)滿足

則認為pAB(tABk)是有效數據，否則應當予以舍棄。(14)式中的εe是可以根據不同的實際情況加以適當選取的正常數。判據(14)式可作為EKF 導航算法中的一個子模塊加以使用。

3 可觀測性分析

可觀測性作為動態系統的重要性質之一，描述了系統的狀態量能否經由量測數據加以求解。由前述討論可知，當主、從AUV 以相同的速度沿同一方向平行航行時，協同導航系統全局不可觀測。本節進一步研究單領航者協同導航系統的局部可觀測性，這在實際應用中更具有普遍意義［11］(在大多數情形下，系統的全局可觀測性條件是難以獲得的)。

定義tAkB時刻關于相對位置量測量rAB，ΔpAB的向量函數

經過一個采樣周期Ttu=tk+1-tk，并結合(15)式可得

即

直接計算映射(16)式的Jacobi 行列式可得

因此，協同導航系統局部可觀測的條件是Jh［k，k+1］≠0，即

分析(19)式知，如果導航系統局部可觀測，當且僅當相鄰的兩個相對位置量測值pAB(tABk)和pAB(tABk+1)線性獨立。利用(19)式可以方便地檢測系統的局部可觀測性:設δ0是一給定的正常數，pAB(tAkB)，pAB(tAkB+1)是相鄰的兩個量測值，如果

則系統不可觀測或近似不可觀測，此時需要調整主、從AUV 的運動軌跡以保持系統的可觀測性，并以此保證定位解算的正確性。

4 仿真結果

為檢驗文中協同導航算法的有效性和實用性，進行仿真分析研究。如圖2所示，AUV1(領航者)由坐標原點出發沿直線航行，AUV2、AUV3 首先按斜線航行一段距離，然后與AUV1 保持平行航行。AUV1 的航速為2 m/s，AUV2 和AUV3 的航速為1 m/s，傳感器采樣周期為1 s.速度信息由多普勒速度傳感器測量，取σ2v=(0.1 m/s)2的零均值高斯白噪聲;航向角信息由陀螺羅經測量，取σ2φ=(0.5°)2的零均值高斯白噪聲;AUV 間的相對位置量測噪聲取σ2r=(0.1 m)2的零均值高斯白噪聲。

圖2 AUV 的仿真運動路徑Fig.2 The simulated trajectories of AUVs

圖3給出了從AUV 的EKF 協同導航算法軌跡。由圖3可知，EKF 協同導航算法軌跡與真實軌跡(見圖2)有較好的吻合性，且在全航程中保持穩定。圖4分別給出了AUV2、AUV3 的協同導航定位誤差。可以看到，在整個航程中，AUV2、AUV3 的定位誤差中值約為2.5 m，單一方向的最大定位誤差不超過5 m，具有較高的導航定位精度。

為進一步檢驗文中導航算法的性能，將文獻［7］中的CN 導航算法、文獻［9］中的LM-EKF 導航算法與文中方法進行比較(見表1)，三種算法的仿真均采用圖2所示的運動路徑和本節所給定的初始條件。

圖3 從AUV 的協同導航軌跡Fig.3 Cooperative navigation trajectories of follower AUVs

圖4 從AUV 的定位估計誤差Fig.4 Localization errors of follower AUVs

表1 三種協同導航算法的性能比較Tab.1 Performance comparison of three cooperative navigation algorithms

由表1可以看出，在相同仿真時間內，文中的導航算法實現了與CN 算法相當的導航定位精度，但所耗費的CPU 計算時間僅為后者的58%.LM-EKF方法首先采用LM 算法優化了EKF 濾波器的初值，因而其定位精度有所提高。但是，LM-EKF 方法所耗費的CPU 計算時間大約是文中方法的2.86 倍，可見其在提高定位精度的同時犧牲了部分導航解算的實時性。相比而言，文中的導航算法較好地兼顧了定位精度與實時性兩方面的要求，在不太損失定位精度的同時有效提高了計算效率。

5 結論

結合單領航者AUV 協同導航系統的定位原理和運動學模型，基于相對位移測量、航位推算信息及相鄰時刻主、從AUV 間相對位置的幾何關系，提出了一種多AUV 協同導航算法。仿真結果表明，基于EKF 的協同導航算法具有較高的定位精度，且與文獻［7，9］中的導航算法相比，有效提高了定位解算的實時性。

References)

［1］ Kinsey J，Eustice R，Whitcomb L.A survey of underwater vehicle navigation:recent advances and new challenges［C］.The 7th IFAC Conference on Maneuvering and Control of Marine Craft，Lisbon，Portugal，2006:1-12.

［2］ Eustice R，Whitcomb L，Singh H，et al.Recent advances in synchronous-clock one-way-travel-time acoustic navigation ［C］.Oceans'06 MTS/IEEE Conference on Exhibition，Boston，USA，2006，1-7.

［3］ Stutters L，Liu H，Tiltman C，et al.Navigation technologies for autonomous underwater vehicles［J］.IEEE Transactions on Systems，2008，38(4):581-589.

［4］ Chandrasekhar V，Winston S，Yoo S C，et al.Localization in underwater sensor networks-survey and challenges［C］.Proceedings of the 1st ACM International Workshop on Underwater Networks，New York，2006:33-40.

［5］ Bahr A，Leonard J，Fallon M.Cooperative localization for autonomous underwater vehicles［J］.The International Journal of Robotics Research，2009，28(6):714-728.

［6］ Baccou P，Jouvencel B，Creuze V，et al.Cooperative positioning and navigation for multiple AUV operations［C］.Oceans'01 MTS/IEEE Conference and Exhibition，Honolulu，2001:1816-1821.

［7］ Bahr A.Cooperative localization for autonomous underwater vehicles［D］.Massachusetts Institute of Technology and Woods Hole Oceanographic Institution，2009.

［8］ Gadre A.Observability analysis in navigation systems with an underwater vehicle application［D］.Virginia Polytechnic Institute and State University，2007.

［9］ Baccou P，Jouvencel B.Simulation results，post-processing experimentation and comparison results for navigation，homing and multiple vehicle operations with a new positioning method using a transponder［C］.Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robotics and Systems，Las Vegas，2003:811-817.

［10］ 秦永元，張洪鉞，汪叔華.卡爾曼濾波與組合導航原理［M］.西安:西北工業大學出版社，2007.QIN Yong-yuan，ZHANG Hong-yue，WANG Shu-hua.Kalman filter and integrated navigation principles［M］.Xi'an:Northwestern Polytechnical University Press，2007.(in Chinese)

［11］ 鄭大鐘.線性系統理論［M］.第2 版.北京:清華大學出版社，2002.ZHENG Da-zhong.Linear system theory［M］.2nd ed.Beijing:Tsinghua University Press，2002.(in Chinese)