經濟圈公路網絡布局優化模型研究＊

易富君 鄧 衛 王 晨 周竹萍

(東南大學交通學院1) 南京 210096) (招商局重慶交通科研設計院有限公司2) 重慶 400068) (江蘇省交通工程建設局3) 南京 210004)

在經濟全球化進程中,城市區域化和區域城市化正在成為城鎮系統演化的一個基本態勢,進而形成了以一個或多個中心城市為核心的經濟圈[1].公路網作為促使經濟圈形成的一個重要條件,在規劃和建設的時候,不但要滿足交通需求,還要追求出行的舒適、安全、快速,以及可持續發展等多項目標[2].本文在分析經濟圈公路網絡布局的要求和特點的基礎上,建立起基于經濟圈公路網絡布局優化特點的多目標雙層規劃布局優化模型.上層規劃為決策者的設計方案,下層規劃為使用者的出行選擇,即交通流量分配.下層不能改變方案,但能根據自身的需要選擇合適的出行路線,上層必須考慮出行信息,綜合路網的基本要求和實際的出行需要對方案進行調整,是一個典型的雙層規劃模型,并應用遺傳-模擬退火混合優化策略算法(GASA)對模型進行求解.

1 經濟圈公路網布局的特點及要求

經濟圈公路網是指連接經濟圈內各城市的公路所構成的公路網絡系統.本文所研究的經濟圈公路網是連接經濟圈內各城市的公路所構成的公路網絡系統,包括連接城市與城市之間的高速公路、一級公路、二級公路、三級公路、四級公路等五類公路.

國家級各類公路網由于路網規模較大、結點層次較高,路網布局的重點是解決結點之間的宏觀通道性運輸聯系問題,因而路網布局主要集中在宏觀層次[3-4].布局的主要任務是確定尚未連通的各結點之間是否連通、連通后的技術等級,以及目前已經連通的各結點之間的路線是否改造、改造后的等級.基于此,文中提出的多目標雙層規劃模型能夠實現經濟圈公路網布局優化的多元要求.

2 雙層布局優化模型

2.1 目標函數及約束條件

由于經濟圈公路網絡建設投資巨大,因此建設運營資金總量成為公路網布局優化問題的一個總量限制,同時為了滿足經濟圈內各個城市間的快速通達性,還需要是路網的連接度最大,即模型上層規劃的目標函數為建設投資金額最少并使路網連接度最大.根據《公路工程技術標準》給出了路段等級、建設費用及其他屬性,如表1所列.表中假定高速公路路段的屬性固定,即在優化過程中屬性不變,不能進行改建.假設路段單位改造費用為改造后單位建設費用與改造前單位建設費用之差,同時上層規劃中還要考慮選擇可行域、服務水平以及迂回率(非直線系數)等約束條件.

可行域約束即給決策變量一個可行范圍,提高搜索效率,文中先確定一個節點與其他節點是否有連接的可能性,排除不能連接的邊,使路網設計在此范圍內進行;服務水平約束即表示在未來OD流量在路網進行分配的時候應滿足一定的服務水平,即V/C比在一定適合的范圍內;迂回率主要是保證經濟圈內的重要節點之間的時間或空間距離不能超過一定的標準.在下一節的雙層規劃模型中將給出每種約束的數學表達式[5-6].

表1 道路等級及其對應值

2.2 模型的建立

由2.1所得到的目標函數及約束條件,建立經濟圈混合公路網絡設計的上層規劃模型如下.

上層規劃模型

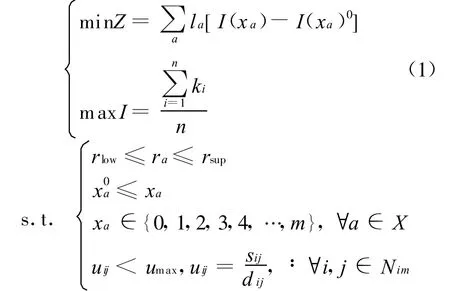
式中：la為路段a的長度;I(xa)為路段a改造后的建設費用;I(xa)0為路段a改造前的建設費用;ki為第i節點所連接的邊數;n為經濟圈內規劃所應連通的節點數;rlow為最小允許的V/C;rsup為最大允許的V/C;為現狀路段a的等級;xa為優化方案中路段a的等級;uij為任意2個重要節點之間的迂回率;umax為允許的最大迂回率;sij為初始可行路網中任意重要節點之間的最短距離;dij為規劃路網中任意重要節點之間的最短距離;Nim為重要節點集.

下層規劃模型

3 基于遺傳-模擬退火混合優化策略的算法(GASA)

3.1 算法求解的關鍵要點

設路網最大可能的路段數為n,則染色體x1, x2,x3,…,xn表示網絡優化的一個方案.其中決策變量為xa=(0,1,2,3,4,5,6,7),對應值如表2所列.

表2 決策變量與對應值

本模型的適應度函數,可采用乘除法將上層規劃問題中的目標函數轉化為式(3)的形式,然后使適應度函數與轉化過后的目標函數對應.

適應度函數主要需滿足單值、連續、非負和最大化等特點,本文采用的適應度函數如下.

式中：V為式(4)右邊第二部分的最大值;O(i)為第i個個體的轉化后目標函數值;N為種群個數.

約束條件處理與算子設計：(1)可行域根據路網的可能連接關系確定備選路段;(2)服務水平采用懲罰函數進行處理,在可行范圍之外的方案進行懲罰;(3)本文采用3個遺傳算子,即復制(選擇)、交叉、變異,其中交叉采用兩點交換的原則,變異采用單點變異.

3.2 計算步驟

步驟1 初始化.根據實際產生各點的可能連接邊,生成初始可能連接圖：(1)設定遺傳算法中的選擇概率 px,交叉概率pc,變異概率pm,每一代產生的種群(染色體)數目N,最大進化代數以及收斂判斷步長,并令初始進化代數g=0;(2)設定模擬退火算法中的內循環次數M,溫度的初始值令

步驟2 對初始方案實施連通性檢查,確定重點節點的連通,并得到各路段的通行能力,設計車速等相關參數.

步驟3 根據模型上層問題的優化目標函數確定合理的適應度函數形式,并確定對模型優化決策變量進行編碼的方式,產生初始種群令g=1.

步驟4 計算各個個體對應的工程造價和路網連接度的比值,即目標函數,對比值進行排序,將比值不大于當前最優值的個體轉入下層規劃進行配流,計算V/C.

步驟5 如果 g＞gmax或 gstop＞gmaxstop,所得染色體即為模型的解,輸出結果,否則轉下一步.

步驟8 退溫,令T=0.5T,轉步驟4.

4 算 例

本文選取了以高速公路和干線公路為主,根據長三角經濟圈簡化現狀道路網絡結構和已有規劃以及專家意見,在現狀道路網絡基礎上選擇5條“可能新建路段”組成經濟圈公路網絡優化的初始可行網絡,如圖1所示.圖中路段屬性包括路段編號和長度.節點1～14為交通小區作用點,節點總數為15個,各節點之間的OD交換量通過預測各交通小區節點的交通生成量后進行交通分布得到.由于篇幅有限,交通小區的OD交換量分布數據和道路技術等級數據略去.

圖1 長三角經濟圈現狀公路網絡優化初始可行網絡

應用遺傳-模擬退火算法求解長三角經濟圈公路網布局優化模型.在優化過程中,種群規模取37,交叉概率和變異概率分別為0.95和0.05,最大進化代數取300,對不滿足約束條件的路段的懲罰系數取該路段的2倍,上層模型中路段負荷約束上限取1,下限取0,當進化至124代時,算法終止得到滿意的優化結果如表3所列,其中路段名稱中的新建路段以連接兩城市名命名.從表中可以看出需新建四條公路,改建二條,總投資額為72.07億元,最大連接度為5.13.

表3 長三角經濟圈公路網絡優化方案

5 結束語

本文將混合公路網設計的雙層規劃模型應用到經濟圈公路網布局規劃中,并將混合網絡設計問題中的連續性網絡設計問題轉化為離散型網絡設計問題,使整個網絡設計問題成為只含離散變量的公路網設計問題.對模型的求解問題,本文運用了在交通系統領域運用最為廣泛的遺傳算法(GA)和模擬退火算法(SA)進行融合而成的遺傳-模擬退火混合算法,并應有MATLAB開發了相應的算法程序,應用實例表明模型及算法的可行性,所以對我國經濟圈公路網的布局優化改善具有重要的理論意義和實用價值.

[1]左 峰.經濟學視野中大城市經濟圈的形成與發展-論中國三大城市經濟圈的現狀與發展[J].華東師范大學學報：哲學社會科學版,2002,34(5)：89-96.

[2]張 偉.經濟圈的概念、特征及其規劃探討[J].城市規劃,2003,127(16)：47-50.

[3]蓋春英.公路網規劃布局優化研究[D].哈爾濱：哈爾濱工業大學交通科學與工程學院,2003.

[4]楊忠誓.公路網絡路線布局優化的雙層規劃模型及算法研究[J].北方交通,2007(11)：42-45.

[5]聶 偉.都市圈道路網絡優化及其評價理論研究[D].北京：北京交通大學交通運輸學院,2007.

[6]劉偉銘,姜 山.基于GASA混合優化策略的雙層規劃模型求解算法研究[J].土木工程學報,2003 (7)：27-32.