基于 ADAMS/Vibration的曲軸受迫振動分析

馬淑英,陳立東,劉榮昌,陳建偉

(河北科技師范學院機電工程學院,河北秦皇島,066600)

曲軸系統作為發動機上主要的運動部件,它的性能優劣直接關系到發動機乃至整車的性能、可靠性和壽命。曲軸系的振動是引發內燃機振動的主要因素。曲軸上作用有大小、方向周期性變化的切向和法向作用力,故曲軸會產生扭轉振動[1]。由于曲軸較長,扭轉剛度較小,且曲軸系的轉動慣量較大,故曲軸扭轉振動頻率較低,在發動機工作轉速范圍內容易產生共振,從而引起較大噪聲、加劇其它零件的磨損,甚至導致曲軸折斷。曲軸的振動本質上是三維形式的振動,不僅扭轉振動是人們研究的主要內容之一,彎曲振動、縱向振動也成為研究的重要內容[2]。因此,開展軸系多維振動的機理與控制方法的研究既有較高的學術價值,又有明確的工程應用意義。

1 曲軸的振動分析方法

由于曲軸的結構和受力情況都比較復雜,在計算曲軸軸系的振動特性時,一般都要將軸系簡化為比較簡單的力學模型,以便于求解。早期的曲軸振動研究主要采用離散化方法,并將曲軸振動作為純扭轉振動處理。目前,多采用 Holzer法、傳遞矩陣法、有限元法、彈性波法、模態分析法等曲軸振動分析方法,其中傳遞矩陣法因計算方便快速應用最廣,有限元法因計算精度高而受人青睞,彈性波傳播法兼具上述兩種方法的特點,開始被引入曲軸振動計算[3]。

2 ADAMS軟件簡介

ADAMS軟件是美國 MDI公司(Mechanical Dynamics Inc.)開發的虛擬樣機分析軟件,它由基本模塊、擴展模塊、接口模塊、專業領域模塊及工具箱 5類模塊組成。用戶不僅可以采用通用模塊對一般的機械系統進行仿真,而且可以采用專用模塊針對特定工業應用領域的問題進行快速有效的建模與仿真分析[4]。

3 曲軸系受迫振動分析

3.1 剛柔耦合曲軸系模型的建立

多柔體系統不同于剛體系統,當多柔體系統中體的彈性不可忽略時,在多體系統的建模和分析當中必須將體的柔性變形考慮進來,考慮部件柔性的多體系統稱為柔性多體系統[5]。多柔體系統動力學是多學科交叉發展的產物,所研究的問題包括了宏觀世界機械運動的主要問題,研究可變形體和剛體組成的系統在經歷大范圍空間運動時的動力學行為[6]。多柔體系統動力學不僅考慮將系統中子部件有些抽象為剛體,計算鉸接處的彈性和阻尼,而且考慮部件的變形,它相比多剛體動力學更側重于研究部件的變形與運動的相互耦合作用所產生的動力學效應。柔體模型的建立方法主要有離散化方法和模態集成法。

3.1.1 模態集成法 模態集成法的基本原理是將柔性體視為有限元模型的節點的集合,相對于局部坐標系有小的線性變形,而此局部坐標系做大的非線性整體平動和轉動[7]。每個節點的線性局部運動近似為模態振型或模態振型向量的線性疊加。如果局部坐標系的位置用它在慣性參考系中的笛卡爾坐標X=(x,y,z)和反映方位的歐拉角 ψ=(ψ,θ,φ)來表示,模態坐標用 q={q1,q2……qm}T(m為模態坐標數)來表示,則柔性體的廣義坐標可選為:

式中,x,y和 z是局部坐標系相對于整體坐標系的空間位置;ψ,θ和 φ是局部坐標系相對于整體坐標系原點的歐拉角;qj是第 m階模態振幅的振型分量。

柔性體第 i個節點的空間位置矢量確定為:

式中,X表示局部坐標系在慣性坐標中的空間位置矢量;A表示局部坐標系相對于慣性坐標系原點的方向余弦矩陣;si表示第 i個節點未變形前在局部坐標系的空間位置矢量;φi表示第 i個節點的移動自由度的模態矩陣子塊;q表示模態振幅向量。將式(1)對時間求導,得到第 i個節點的速度為:

式中,ω表示局部坐標系的角速度向量;B表示將歐拉角對時間求一階導數變為角速度的轉換矩陣;“└”表示向量對應的對稱矩陣;φ′表示第 i個節點的轉動自由度的模態矩陣子塊。節點 i的角速度也可以用物體的剛體角速度與變形角速度之和來表示:ωi=ω+φ′·q。 從上式可以得到動能和勢能的表達式如下:

將上式代入拉格朗日方程,就可得到 Adams的柔性體方程式如下:

在此柔性體方程式中,K和 D分別為柔性體的模態剛度和阻尼矩陣,剛度和阻尼的變化只取決于變形。因此,剛體的平動和轉動對變形能和能量損失沒有影響。重力寫成 fg。λ為約束方程的拉格朗日乘子,ψ和 Q為外部施加的載荷。對柔性體方程的求解,首先采用 Newton-Raphson算法迭代將其展開。展開中產生的稀疏矩陣,采用吉爾 Gear剛性積分方法可以實現高效求解。方程式(5)中的質量矩陣是變形和方向的復雜函數,但通過確定 9個慣性常量,計算速度將會有很大提高。

3.1.2 集成有限元模型的多體理論分析 在有限元分析中,分析對象劃分的網格節點,是相對于對象本身的某一慣性坐標。為了描述方便,一般將慣性坐標固定連在物體的一端,并將坐標的一個軸線與物體的軸線重合[9]。將有限元分析的柔體加入多體系統中,需將柔體作相對的位移,即需將柔體分析的有限元方程乘以轉換矩陣,從而實現由局部坐標向整個模型的慣性坐標的轉換。

采用拉格朗日方法建立的多體系統動力學,當代入其各項因子后,其簡化形式如有限元方程:

式中,M=BmeBT,me為靜止狀態下的單元質量矩陣;C=BceBT,ce為靜止狀態下的單元阻尼矩陣;K=BkeBT,ke為靜止狀態下的單元剛度矩陣。有限元模型的通用結構分析方程,一般是在有限元分析對象的局部坐標系下建立的。方程中的變量是相對于局部坐標的坐標元素。為了實現有限元分析方程與多體系統動力學分析方程的統一,可以通過多體理論中坐標轉換矩陣 B,實現有限元分析方程向多體系統動力學的轉換。對于形如上式的有限元方程,其慣性坐標下的剛度、阻尼、質量矩陣,是由局部坐標系的響應矩陣乘以局部坐標向慣性坐標的轉換矩陣得到的。即上述方程可以表示為:

同時,上述方程的等號右邊也可以表示為位移、速度、加速度的函數:

當單元的位移不大時,采用慣性坐標描述方程應是簡單可行的方法,因為轉換矩陣不需要更新。但當單元位移較大時,轉換矩陣必須更新,從而使得局部坐標向慣性坐標系轉換的相關矩陣也必須更新,如此系統的求解效率就明顯降低。

在 Adams軟件中,所有的剛體與柔體都使用一個隨剛體和柔體運動的浮動局部坐標(Local Floating Reference Frame),當剛體或柔體運動時,對于系統求解的每一步,從局部坐標向慣性坐標系轉換的相關矩陣也必須更新,但慣性坐標系下的矩陣不需要重新形成,從而提高了系統的求解效率。對于集成有限元模型的多體系統的求解是在多體模型的基礎上,預先求得柔性體與多體系統的作用點的力、力矩、位移、速度、加速度等邊界條件,柔性體以此邊界條件求出變形與力、力矩,與多剛體模型的結果進行對比,如果誤差較大,可進入下一步求解,此時以柔性體的變形或力、力矩為已知條件,求得系統對此作用點相應的力、力矩或位移,直到誤差達到規定的范圍。

3.2 曲軸受迫振動分析

3.2.1 曲軸扭轉振動產生的機理 當柔性軸受到外界扭轉力矩作用時,會產生彈性變形,這種變形的絕對值在一般情況下是不大的,但是當外界扭轉力矩的頻率與軸的共振頻率相同時,軸的扭轉變形幅度將大大超過正常值,這種現象就是軸的扭轉共振[8]。

由于曲軸系本身不僅具有慣性,而且還有彈性,由此確定了其固有的自由振動特性。曲軸本身是由連桿作用在各個曲拐上的周期變化的扭矩 M驅動旋轉的,它是由作用在活塞上的氣體壓力所產生的扭矩 Mg和由往復慣性力所產生的扭矩 Mj復合而成的。雖然這兩個扭矩都是周期變化量,但都不是按簡諧規律變化的,因此可以用數學方法分解成一系列簡諧量之和。當在某一轉速下,施加在曲軸上的周期變化的某一階簡諧力矩與曲軸本身的扭轉振動頻率相同時,曲軸就會產生所謂的共振現象。

3.2.2 曲軸強迫扭轉載荷的施加 曲軸系存在阻尼,會使自由扭轉振動逐漸衰減,直到振動停止。系統要維持持續振動,必須從外界輸入能量,以彌補阻尼所消耗的能量。在干擾力矩的作用下的持續振動,稱為強迫振動。干擾力矩對系統的作用取決于干擾力矩的大小和它隨時間變化的規律。其中干擾力矩隨時間變化的規律在許多情況下顯得更為重要。作用在發動機曲軸系統上的干擾力矩,一般都是按周期性規律變化的,可以分解為傅立葉三角級數的形式,利用線性系統所滿足的疊加原理,分別考慮其中各次諧波干擾力矩對傳動系統所產生的作用,然后再疊加起來確定系統的振動規律。

干擾力矩的計算公式:

式中,MG為燃氣爆發壓力產生的力矩;Mj為往復慣性力產生的力矩;α為以上止點為基準的曲柄轉角;β為連桿中心線與汽缸中心線之間的夾角;R為曲柄半徑。

在傳統的曲軸扭轉強迫振動分析中,利用傅立葉級數把周期性變化的燃氣爆發壓力產生的力矩 MG展開為扭矩的平均值和一系列具有不同振幅、不同頻率、不同初相位的簡諧力矩之和,然后施加在曲軸上。發動機曲柄連桿機構的慣性力有離心慣性力和往復慣性力兩種。由于離心慣性力通過曲軸的回轉中心,對曲軸不產生扭轉振動的激振力矩。而往復慣性力和燃氣壓力一樣,它們作用在活塞及連桿上,并通過連桿傳到連桿軸頸,對曲軸產生周期性變化的切向力矩,此力矩會激起曲軸系統的扭轉振動。

3.2.3 曲軸強迫扭轉載荷的分析 利用前面建立的完整曲軸系仿真分析模型,可以在 Adams/Vibration中實現對曲軸系的強迫扭轉振動分析,既能提高工作效率又有較高的分析精度。作用在曲軸系的外力主要是燃氣爆發壓力,同時還需要考慮活塞與氣缸的摩擦。燃氣爆發壓力通過示功圖得到,按照發動機的工作順序 1-3-4-2施加在活塞頂部(圖 1)。

圖 1 發動機燃氣爆發壓力

將圖 1所示各缸爆發壓力施加于各活塞頂部,活塞將力傳給連桿,連桿最終將力施加給各連桿軸頸。從曲軸自由端向右,連桿軸頸依次編號 1,2,3,4,則各連桿軸頸處受力如圖 2所示。

在 ANSYS中生成曲軸模態中性文件,導入 ADAMS/View中創建曲軸柔性體模型,將建立的曲軸軸系多剛體動力學模型中的剛性曲軸替換為柔性曲軸。施加爆發壓力和控制曲軸轉速后,即生成曲軸軸系柔性多體動力學模型。對曲軸軸系柔性多體動力學模型進行發動機穩定工況下的動力學仿真,得到曲軸在一個工作周期內的仿真數據(圖 3,圖 4)。

圖 3是第二曲柄臂與第一連桿軸頸之間圓角處的合位移變形曲線,其變形主要是由于第一缸爆發壓力所引起的。圖4是此圓角處變形的合速度變化曲線。由圖 3和圖 4可知:(1)柔性曲軸在受迫振動的初始階段會有較大的振幅波動,但這一時間持續很短,一般在曲軸旋轉第 1周的時間之內,之后曲軸振幅趨于穩定;(2)柔性曲軸在受迫振動的初始階段由于受到來自連桿的瞬時沖擊力,速度變化很快,速度變化波動比較大。但持續時間也很短,一般是在曲軸旋轉 1周的時間之內完成波動,之后速度變化趨于穩定。

圖 2 連桿軸頸受力

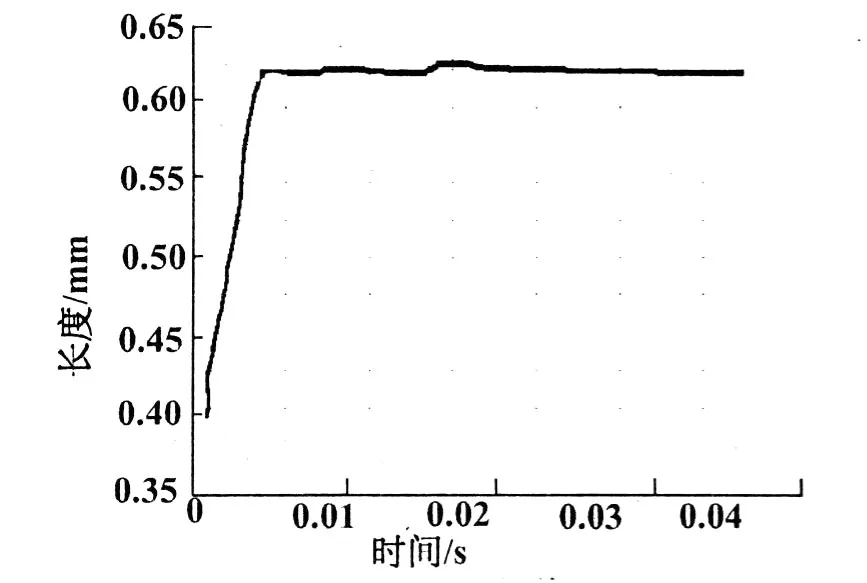
圖 3 合位移

圖 4 合速度

4 結 論

在建立了剛柔耦合曲軸系模型的基礎上,按照給定的加載方式,對發動機曲軸系的扭轉振動做了動態仿真分析。仿真結果表明,在給定加載條件下,曲軸在圓角處的合位移及合速度有一突變,即圓角處所受振動劇烈,易產生變形,與實際相符。利用本分析方法所得到的曲軸受迫震動仿真分析結果,可用于后續的曲軸振動噪聲分析計算。

[1] CLARK,NIJEL.Operation ofa Small Bore Two-Stroke Linear Engine[J].ASME,1998:251-262.

[2] 尤小梅.發動機曲軸動力學仿真[D].沈陽:沈陽理工大學,2004.

[3] 李震,桂長林,孫軍.內燃機曲軸軸系振動分析研究的現狀、討論與展望[J].內燃機學報,2002,2(5):469-474.

[4] 陳立平,張云清,任衛群,等.機械系統動力學分析及 ADAMS應用教程[M].北京:清華大學出版社,2005.

[5] 劉景陽,洪嘉振.柔性體的剛柔耦合動力學分析[J].固體力學學報,2002,23(2):159-166.

[6] 葉先磊,史亞捷.ANSYS工程分析軟件應用實例[M].北京:清華大學出版社,2003.

[7] A R Mc Health,PM Namara.Crankshaft Stress Analysis Combination of Finite Elementand Classical Analysis Techniques Trans ASME JEng[J].Fro Gas Turbines and Power,1990,112(7):268-275.

[8] 祝效華,廖偉志,黃永志,等.CAD/CAE/CFD/VPT/SC軟件協作技術[M].北京:中國水利水電出版社,2004.

[9] 雷宣揚.內燃機曲軸動態振動特性模擬及其裂紋故障分析[D].大連:大連理工大學,2003.

(責任編輯:石瑞珍)