研究阻尼復合圓柱殼振動功率流的一種新方法

張森森 左君偉 張俊杰

1海軍裝備部沈陽局，遼寧沈陽 110031

2駐沈陽導彈專業軍代表室，遼寧 沈陽 110031

3中國艦船研究設計中心，湖北 武漢 430064

研究阻尼復合圓柱殼振動功率流的一種新方法

張森森1左君偉2張俊杰3

1海軍裝備部沈陽局，遼寧沈陽 110031

2駐沈陽導彈專業軍代表室，遼寧 沈陽 110031

3中國艦船研究設計中心，湖北 武漢 430064

減少圓柱殼振動和噪聲的一種有效方法是在其表面敷設阻尼層，這種復合結構稱為阻尼復合圓柱殼。分別運用薄殼理論和彈性理論描述了阻尼復合圓柱殼的內殼和阻尼層，并在此基礎上提出了計算阻尼復合圓柱殼振動功率流的一種新方法。通過數值計算，得到了內外殼體厚度對復合圓柱殼振動功率流的影響規律，為圓柱殼減振降噪措施的應用提供了理論基礎。

復合圓柱殼；振動功率流；傅立葉變換；彈性理論；減振降噪

1 引言

圓柱殼結構的減振降噪是一個熱點問題。為了降低圓柱殼的振動噪聲，一種行之有效的方法之一就是對圓柱殼進行表面處理［1］，而進行表面處理的方法之一就是在圓柱殼表面敷設自由阻尼層，這種復合結構稱為阻尼復合圓柱殼。

建立阻尼復合圓柱殼耦合方程的方法有多種，對阻尼層運動方程的建模也有多種方法。Laulagnet［2］在研究流場中敷設柔性層（阻尼層）復合圓柱殼的輻射聲功率中，將柔性層簡化為沒有質量的阻尼彈簧模型，其阻尼層建模較粗糙。接著，其又運用Taylor展開彈性Navier方程的方式對阻尼層進行了處理［3］。該處理方法僅在阻尼層厚度與其縱波波長的比值遠小于1時成立，因此，只適用于低頻范圍。嚴謹［4］用等效法研究了復合圓柱殼的阻尼層，可以認為，該方法只考慮了阻尼層剛度的貢獻。Ko［5］1483運用彈性方程對阻尼復合圓柱殼的內殼和阻尼層進行了處理，這對研究阻尼復合圓柱殼頗具啟發意義。本文分別運用薄殼Flügge理論和彈性Navier方程來描述復合圓柱殼的內殼和阻尼層運動方程，對于彈性Navier方程，則借助Pathak［6］的方法直接處理。因此，相對于運用三維漸進Taylor展開處理阻尼層的方法建立的阻尼復合圓柱殼模型來說，本文提出的計算阻尼復合圓柱殼模型的適用范圍更廣。由于振動功率流不僅要考慮力作用點處的速度大小，而且還要考慮力與速度之間的相位關系，因此，在數值計算部分，通過改變內殼和阻尼層的厚度，討論了厚度對復合圓柱殼振動功率流的影響。

2 模型介紹和理論推導

2.1 模型介紹

流場中無限長阻尼復合圓柱殼的幾何、材料參數與坐標系如圖1所示。為便于描述，將阻尼復合圓柱殼內殼、阻尼層和外部流場分別標識為1，2，3。設h1、h2分別為內殼和阻尼層厚度，內殼內表面的半徑為R1，內殼與阻尼層的交界面半徑R12=R1+h1，阻尼層與流場的交界面半徑R23= R12+h2，記R=（R1+R12）／2。用r，θ，x分別表示柱坐標系的徑向、周向和軸向，w，ν，u分別表示這3個方向的位移分量。

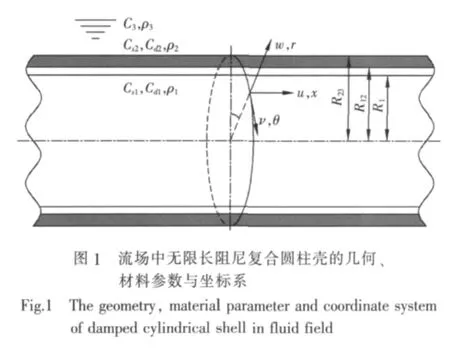
2.2 Flügge殼體方程推導

圓柱殼的運動方程用Flügge殼體理論描述為：

式中，Lij為Flügge殼體微分方程算子；｛u｝=（u，ν，w）T；ν1表示泊松比；E1為楊氏模量；h1為殼體厚度；｛σ｝=｛σtx，σrθ，σrr｝T，是阻尼層施加給殼體的分布作用力。考慮到殼體只受法向外力的作用，此時，｛F｝=｛0，0，Fr｝T。

為便于求解，引入如下傅立葉變換對：

式中，kx表示軸向波數。

運用式（2）對式（1）做傅立葉變換，經過推導，得到如下式子：

式中，［T］為一個3×3的矩陣，其具體表達式省略；上標1表示內殼（以下同）。

2.3 Navier殼體方程推導

對于阻尼層Navier運動方程和外部流場的控制方程，運用傅立葉積分變換和勢理論方法，可得到如下形式的解：

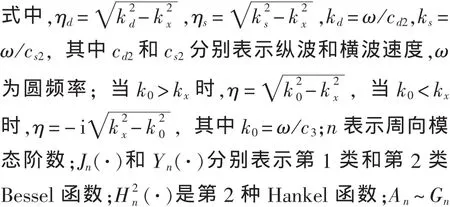
2.4 外 力

設外加力作用在殼體內表面，并且只考慮在x=0截面上作用線分布的徑向激勵力，此力沿圓周按余弦規律分布，可以表示為：

式中，F0為激勵力幅值；δ為delta奇異函數。

3 阻尼復合圓柱殼邊界條件求解

1）在內殼與阻尼層的交界面上r=R12，阻尼層對內殼的法向應力和切向應力可以看成是阻尼層對內殼的分布作用力，共3個邊界條件。

2）在內殼與阻尼層交界面上r=R12，法向位移和切向位移連續，共3個邊界條件；

3）在阻尼層與流場的交界面上r=R23，周向和軸向應力分量為0，法向應力連續，法向位移連續，共4個邊界條件。

可見，邊界條件和待定系數均為10個，耦合方程可以求解。由于推導過程直接，這里將不給出耦合方程的表達式。

4 阻尼復合圓柱殼的振動功率流

振動功率流能全面評價外力對結構的作用。根據功率流定義，在求出內殼內表面的位移后，振動功率流Pin便可求出，無量綱化Pin得到：

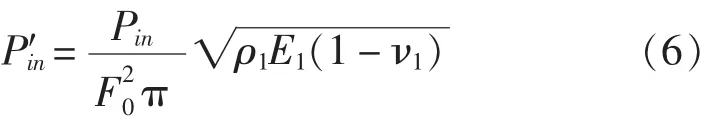
為了比較阻尼層對圓柱殼振動功率流的影響，定義如下無量綱振動功率流插入損失LP：

式中，P′in1和P′in2分別為單層圓柱殼和敷設阻尼的復合圓柱殼無量綱振動功率流。

5 數值計算及結果討論

數值計算中用到的殼體材料參數見文獻［5］1488。設阻尼復合圓柱殼內殼內表面半徑R1=2.540 m，外力幅值F0=1 N。對于單層圓柱殼，去掉阻尼復合圓柱殼阻尼層即可。

1）內殼厚度相同、阻尼層厚度不同時的振動功率流和插入損失。

圖2比較了在周向模態n=1時，不同阻尼層厚度對振動功率流P′in和振動功率流插入損失LP的影響。圖例中的數值表示厚度半徑比（百分號省略），括號中的英文表示對應的殼體理論。例如，2＿6（Flügge＿Navier）表示阻尼復合圓柱殼內殼和阻尼層的厚度半徑比分別為2%和6%（相應的厚度分別為h1=0.050 8 m和h2=0.152 4 m），阻尼復合圓柱殼內殼和阻尼層所用的殼體理論分別是Flügge殼體理論和Navier殼體理論。由圖2可知，增加阻尼層的厚度，振動功率流的峰值便也增加；當內殼的厚度比阻尼層的厚度要厚時，阻尼層的厚度對阻尼復合圓柱殼振動功率流的影響很小。從無量綱振動功率流插入損失LP與頻率的關系圖可看出，在低頻段，不同阻尼層厚度對阻尼復合圓柱殼振動功率流插入損失的影響趨勢是一致的。在高頻段，曲線出現了周期性的峰值，這些峰值的出現是由于阻尼層厚度等于阻尼層縱波波長1/2整數倍［5］1490的原因。具體為：當激勵頻率、阻尼層厚度和縱波波長滿足式（8）的關系時，對應的頻率點將出現峰值：

式中，λ為阻尼層縱波波長。

把波長與波速和頻率的關系代入式（8）得：

當h2＝0.050 8 m時，f＝2 000a，具體值為：

f＝2 000 Hz，4 000 Hz，6 000 Hz…，

當h2＝0.152 4 m時，f＝2 000 a，具體值為：

f＝667 Hz，1 333 Hz，2 000 Hz，2 667 Hz…，

2）內殼厚度不同、阻尼層厚度相同時的振動功率流和插入損失。

圖3比較了在周向模態n＝1時，不同內殼厚度對振動功率流P′in和振動功率流插入損失LP的影響。從圖3可看出，增加內殼厚度能明顯降低阻尼復合圓柱殼的振動功率流。從振動功率流插入損失圖中可看出，在中低頻段，當內殼的厚度增加時，阻尼層對阻尼復合圓柱殼振動功率流的影響程度變小；在高頻段，阻尼層對阻尼復合圓柱殼的振動功率流影響較小。

6 結論

本文對建立的阻尼復合圓柱殼模型的內殼和阻尼層分別用Flügge理論和彈性Navier方程予以了描述，通過運用傅立葉積分變換和勢理論，直接得到了耦合方程的解。通過改變內殼和阻尼層的厚度，得到了厚度對復合圓柱殼振動功率流的影響，結論如下：

1）當阻尼復合圓柱殼的內殼厚度相同時，增加阻尼層厚度，振動功率流的峰值也增加；與阻尼層相比，當內殼的厚度要厚些時，阻尼層的厚度對阻尼復合圓柱殼振動功率流的影響較小。在高頻段，阻尼層對阻尼復合圓柱殼振動功率流的影響較小，并且曲線出現了峰值，這些峰值的出現是由于阻尼層厚度等于阻尼層縱波波長1／2整數倍的原因。

2）當阻尼復合圓柱殼的阻尼層厚度相同時，增加內殼厚度可明顯降低振動功率流。在中低頻段，當內殼厚度增加時，阻尼層對阻尼復合圓柱殼振動功率流的影響程度變小；在高頻段，阻尼層對阻尼復合圓柱殼的振動功率流影響較小。

［1］ 陳美霞，駱東平，曹鋼，等.有限長加筋雙層圓柱殼低階模態聲輻射性能分析 ［J］.哈爾濱工程大學學報，2004，25（4）：446-450.

［2］ LAULAGNET B，GUYADER J L.Sound radiation from a finite cylindrical shell covered with a compliant layer［J］.Journal of Vibration，Acoustics，Stress and Reliability in design，1991，113（2）：267－272.

［3］ LAULAGNET B，GUYADER J L.Sound radiation from finite cylindrical coated shells，by means of asymptotic expansion of three－dimensional equations for coating［J］.The Journal of the Acoustical Society of America，1994，96（1）：277－286.

［4］ YAN J，LI F C，LI T Y.Vibrational power flow analysis of a submerged viscoelastic cylindrical shell with wave propagation approach［J］.Journal of Sound and Vibration，2007，303（1/2）：264－276.

［5］ KO S H，SEONG W，PYO S.Structure－borne noise reduction for an infinite，elastic cylindrical shell［J］.Journal of the Acoustical Society of America，2001，109（4）：1483－1495.

［6］ PATHAK A G，STEPANISHEN P R.Acoustic harmonic radiation from fluid－loaded infinite cylindrical elastic shells using elasticity theory［J］.The Journal of the Acoustical Society of America，1994，96（1）：573－582.

A New Method for Calculating Vibration Power Flow ofDamped Cylindrical Shell

Zhang Sen-sen1 Zuo Jun-wei2Zhang Jun-jie3
1 Department of Naval Equipment，Shenyang Division，Shenyang 110031，China
2 The Military Representative Office for Guided Missiles，Shenyang Division of Department of Naval Equipment，Shenyang 110031，China
3 China Ship Development and Design Center，Wuhan 430064，China

An effective way to decrease the vibration and noise of cylindrical shell is to coat the shell with damp layer，known as＂damped cylindrical shell＂.The motion equations of the inner shell and coated layer of the damped cylindrical shell are described by the thin shell theory and elastic equations respectively，and a new method for calculating the vibration power flow is proposed.Through changing the thickness of the inner shell and coated layer，the influence of thickness to the vibration power flow is concluded.

damped cylindrical shell；vibration power flow；Fourier transform；elastic equation；vibration/noise reduction

U661.44

A

1673－3185（2011）02－52－04

10.3969/j.issn.1673-3185.2011.02.010

2010-09-14

張森森（1977－），男，工程師。研究方向：減振降噪。E-mail：ssza521345@163.com