群時延內均衡的模擬濾波器優化設計

李 鵬,馬紅梅

(華北科技學院,北京 101601)

1 引 言

群時延是濾波器最重要的性能指標之一,反映相位隨頻率變化的快慢,其理想狀態為一條水平直線,其值應該是一個常數。在信號的傳輸過程中,如果群時延波動過大,會使信號產生畸變,對數字信號而言,因為相鄰碼元之間不同頻率分量通過群時延濾波器之后的時延不同,導致接收方接收到的信號會在相鄰碼元之間產生串擾,增加誤碼率[1]。用網絡綜合法設計的濾波器的群時延波動非常大,如何取得濾波器理想的帶外衰減和較小的帶內群時延,常常是濾波器設計的難點[2]。一般的解決辦法是用時延均衡器來均衡。普通濾波器的群時延特性猶如鍋底狀,如果外加均衡器來“補平”則叫做外均衡,在濾波器內部采用特殊措施實現群時延均衡的稱為內均衡。無論是內均衡還是外均衡,雖然能夠使群時延波動相對變小,但是時延均衡器的參數是固定的,只能被動地相對減小群時延波動,而不能從根本上解決帶內群時延波動過大的問題。另外,加入均衡都會增加整個濾波器的元件數量,以致增大體積,加大損耗,增加成本[3]。

隨著現代高質量通信系統的發展,不僅要求濾波器幅頻響應滿足特定的指標,同時還要求在通帶內具有較小的群時延特性。而相頻特性和幅頻特性之間又存在著矛盾,為使濾波器的幅頻特性和群時延特性在合理折衷的條件下各自達到最佳狀態,本文提出了一種群時延內均衡的濾波器優化設計方法。首先根據設計指標先對濾波器的幅頻特性進行優化,然后內接時延均衡器,在通帶內用最小二乘法擬合一條水平直線作為理想曲線的初值,然后優化元件參數,使群時延特性曲線向這條直線逼近,同時優化整個濾波器的幅頻特性。重復上面的過程,直到獲得最佳的元件參數為止[4]。

本文中實例的幅頻特性的設計已經發表在文獻[4]中,在網絡綜合法設計的濾波器基礎上,利用作者提出的極點放置技術和優化技術先使濾波器的幅頻特性算術對稱[1],再內接二階時延均衡器,最后同時優化幅頻特性和群時延特性,降低群時延的波動。

2 時延均衡器直接耦合

利用文獻[4]提出的極點放置技術和優化技術設計出來的濾波器雖然幅頻特性能達到算術對稱,但相頻特性很難接近線性,為解決此問題,需要在電路中加時延均衡器。一階均衡器僅有一個設計參數,對群時延的均衡效果有限,所以一般都選用二階均衡器。二階均衡器有兩個設計參數 Wr和Q,Wr是群時延最小值處的頻率,Q是濾波器的品質因數。通常要根據Wr和Q來計算二階均衡器的各個元件參數。本文采用內均衡方式直接耦合時延均衡器[5]。

3 幅頻和群時延特性模型的建立

3.1 濾波器幅頻特性目標函數的建立

濾波器幅頻特性的數學模型在文獻[4]中已經給出 ,即:

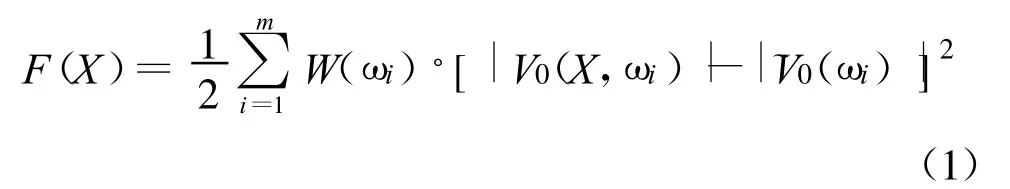
3.2 群時延特性目標函數的建立

建立濾波器群時延特性數學模型,先在通帶內取p個頻率點,然后求各個頻率點群時延的實際值與理想值之差的平方和,目標函數可以寫成:

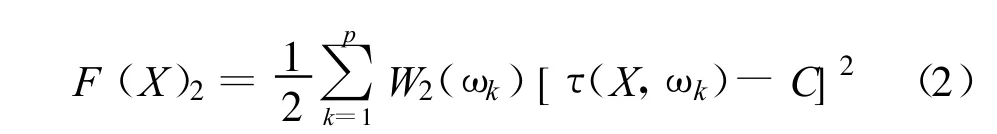
式中,W2(ωk)為各頻率點 ω′1,ω′2,ω′k,…,ω′p上相頻特性的權重函數;τ(X,ωk)為各個頻率點上實際的群時延值,其值可由相位求導得到;C為理想的群時延特性曲線,其值為一常數。

3.3 濾波器總目標函數的建立

濾波器總的目標函數就是幅頻特性目標函數與群時延特性目標函數之和,即:

4 濾波器的優化

4.1 目標函數的梯度

對目標函數進行優化,首先要求出目標函數的梯度。幅頻目標函數的梯度在文獻[4]中已經給出,對群時延特性的梯度,因為群時延是相位對頻率的一階導數,為使編程方便,所以把群時延的梯度轉換為對相位的梯度,即:

式中,τp為相位延遲,φ為相位,ω為角頻率。轉換后的梯度為

4.2 優化過程

對于群時延特性,需要將目標函數向一個常數優化,這個常數可以由最小二乘法求得。對總的目標函數,利用無約束最優化方法可以使目標最小,此時幅頻特性接近于理想狀態,群時延接近于常數。

5 實例分析

以設計一個無源帶通濾波器為例,中心頻率是490MHz,3 dB帶寬為70MHz,線性坐標下±90MHz處衰減大于55 dB,矩形系數小于2.5,群時延波動小于12 ns,兩端接電阻都是50Ψ。

6 網絡綜合法設計

6.1 幅頻特性設計

對濾波器幅頻特性的設計,采用六階電容耦合諧振濾波器,具體電路和參數以及幅頻特性在文獻[4]中已經給出。圖1為通帶內的群時延特性曲線。

圖1 濾波器的群時延特性Fig.1 Group-delay of the filter

6.2 時延均衡器直接耦合

從圖1可以得出,通帶內群時延波動的最大值是35.05 ns,在峰值處的頻率為499.69 MHz,再根據二階時延均衡器的設計公式可以得出Q的大概值為[5]27.51。耦合時延均衡器后的電路如圖2所示。

圖2 時延均衡器直接耦合電路Fig.2 Filter circuit coupledwith group-delay equalizer

時延均衡器直接耦合后,幅頻特性基本保持不變,群時延特性如圖3所示。

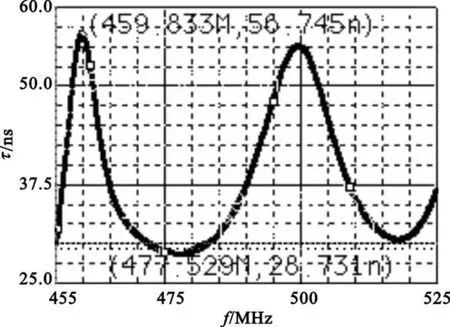
圖3 時延均衡器直接耦合后的群時延特性Fig.3 Group-delay of the filter coupled with group-delay equalizer

由仿真可以得出,在490±35 MHz處的衰減分別為10.968 dB和0.2647 dB,在 490±90MHz處的衰減分別為76.383 dB和47.698 dB,通帶內群時延的最大波動為28.014 ns,此時濾波器的通帶偏向高頻處且不算術對稱。

7 優化設計

7.1 幅頻特性的優化

優化法設計時延濾波器,首先利用極點放置技術對電路進行改進,然后再對濾波器的幅頻進行優化。改進后的電路及優化后的幅頻特性參見文獻[4]中的圖4和圖5,群時延特性如圖4所示。

圖4 幅頻優化后的群時延特性Fig.4 Group-delay of the filter′s amplitude-frequency optimized

7.2 時延均衡器直接耦合

從圖4可以看出,通帶內群時延波動的最大值是23.617 ns,在峰值處的頻率為489.403MHz,再根據二階時延均衡器的設計公式可以得出 Q的大概值為18.156[5]。耦合時延均衡器后的電路和群時延特性如圖5和圖6所示,此時濾波器的幅頻特性基本不變,通帶內群時延波動的最大值減小到16.584 ns。

圖5 改進的時延均衡器直接耦合電路Fig.5 Improved filter circuit coupledwith group-delay equalizer

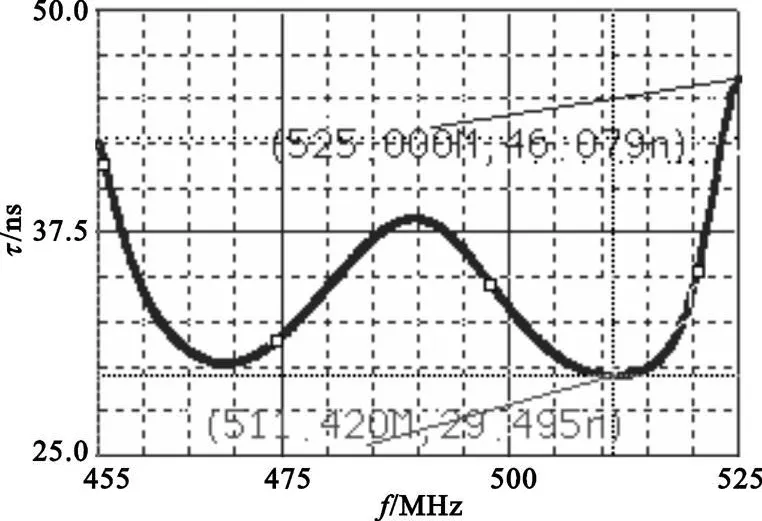
圖6 時延均衡器直接耦合后的群時延特性Fig.6 The filter′s group-delay coupled with group-delay equalizer

7.3 電路整體優化

對整個電路的幅頻特性和群時延特性同時進行優化,優化后的曲線分別如圖7和圖8所示。

圖7 優化后的幅頻特性Fig.7 Amplitude-frequency optimized

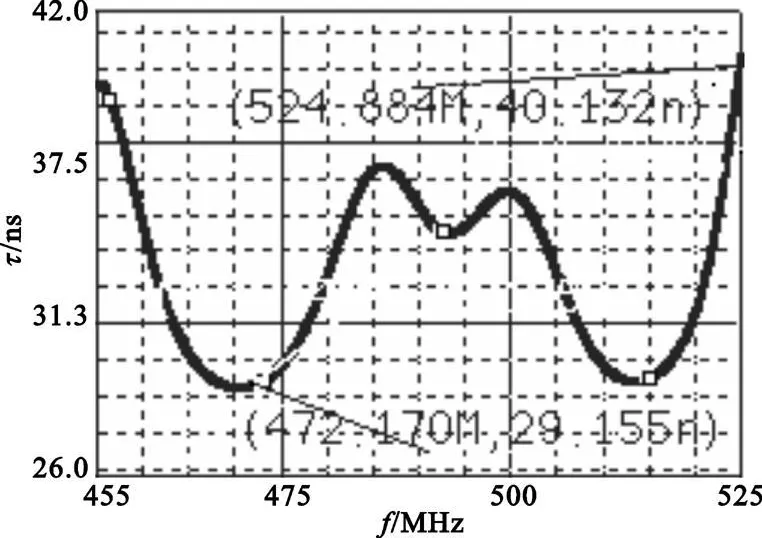
圖8 優化后的群時延特性Fig.8 Group-delay optimized

由仿真可以得出,在490±35 MHz處的衰減分別為2.0492 dB和0.554 dB,在490±90MHz處的衰減分別為55.901 dB和60.355 dB,通帶內群時延的最大波動為10.977 ns。

8 結 論

Pspice仿真結果表明,用網絡綜合法設計的內接時延均衡器的濾波器,其通帶內群時延最大波動為28.014 ns,幅頻特性在線性坐標下不對稱;優化后的幅頻特性基本上是算術對稱的,通帶內群時延最大波動為10.977 ns,只有網絡綜合設計法的39.18%。設計實例表明,優化設計方法相比于網絡綜合設計方法來說,不但能夠使幅頻特性和群時延特性達到合理的折衷,而且能夠解決網絡綜合設計方法難以實現的線性群時延設計問題,具有良好的工程應用價值。

[1]王大壽,趙濤.LC濾波器的小型化制作與生產[J].大連海運學院學報,1994,20(4):60-66.WANG Da-shou,ZHAO Tao.The miniaturization make of the LC filters[J].Journal of Dalian Marine College,1994,20(4):60-66.(in Chinese)

[2]江山.窄帶小群時延波動晶體濾波器設計[J].電訊技術,2010,50(3):54-58.JIANG Shan.Design of Narrow band Little Ripple Group delay Crystal Filter[J].Telecommunication Engineering,2010,50(3):54-58.(in Chinese)

[3]沙海.衛星導航系統傳輸信道的群時延測量方法研究與應用[D].長沙:國防科技大學,2009.SHA Hai.Research andApplication of the Group Delay Measurement Method in Transfer Channel of Satellite Navigation System[D].Changsha:National University of Defense Technology,2009.(in Chinese)

[4]李鵬,馬紅梅.幅頻算術對稱無源帶通濾波器的優化設計[J].電訊技術,2010,50(6):105-108.LI Peng,MA Hong-mei.Optimization Design of Amplitude-frequency Arithmetic Symmetry Passive Bandpass Filter[J].Telecommunication Engineering,2010,50(6):105-108.(in Chinese)

[5]阿瑟·B·威廉斯.電子濾波器設計手冊[M].北京:電子工業出版社,1986:201-208.Arthur B Williams.Design Handbook of Electric Filter[M].Beijing:Publishing House of Electronic Industry,1986:201-208.(in Chinese)