有限群直積的自同構群

秦 鑫，雒曉良

(呂梁學院數學系,山西離石033000)

有限群的自同構群是群論中一個重要而又困難的研究課題,目前十分活躍。由于有限群自同構群研究的困難性和復雜性,往往需要從研究一些特殊群的自同構群入手。由Bidwell,Curran,Mc－Caughan三人合作在2006年發表的文獻[1]中,研究了兩個有限群直積G=H×K的自同構群,定義了A,B,C,D的四個特殊子群,滿足

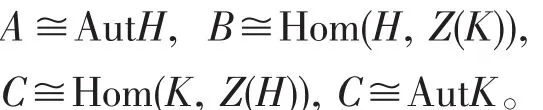
并且證明了一個重要結果(即文獻[1]中定理3.2和定理3.6):如果H和K沒有同構的直因子，則AutG=ABCD。

然而,文獻[1]并沒有徹底解決AutG=ABCD的判別問題,僅僅是給出了一個充分條件。本文在文獻[1]的基礎上,繼續研究群直積的自同構群;通過深化自同構的矩陣表示技術,得到了一個簡明的充要條件。

最后,我們對本文所使用的群論符號作一些說明,與文獻[1]略有不同。

設φ∶H→K為群同態,本文采用群論中通常的記法,將h∈H在φ下的像記為hφ;從H到K的所有群同態構成的集合記為Hom(H,K);用EndH表示H的自同態集合。當K為交換群時,熟知Hom(H,K)在同態的加法運算下構成一個群,其零元為零同態0,而φ∈Hom(H,K)的負元-φ,則定義為h-φ=(h-1)φ=(hφ)-1。

此外,如無其它說明,本文所使用的其余符號都是標準的,可參考文獻[2]或文獻[3]。

1 基本引理

首先給出兩個有限群的直積的自同構之矩陣表述。

設H和K均為有限群,令

為相應的群直積,熟知G中的群運算按如下分量定義:

任取φ∶G→G為G到G的一個映射，令

則映射φ唯一確定了四個與其相伴的映射:

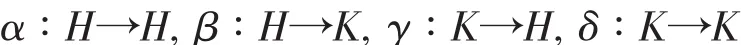
簡單起見,可將其記為矩陣形式:

使用該矩陣記號,在文獻[1]中首先給出了φ為G的自同態的一個刻劃。

引理1[1]φ∈EndG當且僅當與其相伴的映射α,β,γ,δ滿足下述六個條件:

(1)α∈EndH,

(2)β∈Hom(H,K),

(3)γ∈Hom(K,H),

(4)δ∈End(K),

(5)[lmα,lmγ]=1，即α和γ的像在H里相互中心化，

(6)[lmβ,lmδ]=1，即β和δ的像在K里相互中心化。

方便起見,當上述映射φ為群G的自同態時,在本文中我們直接記

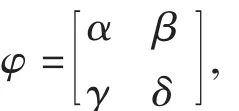
稱之為φ的矩陣表示,其中映射α,β,γ,δ滿足引理1中的六個條件。此時,對任意h∈H,k∈K，注意到在G中有 (h,k)=(h,1)(1,k)，按φ的矩陣表示之含義,再記

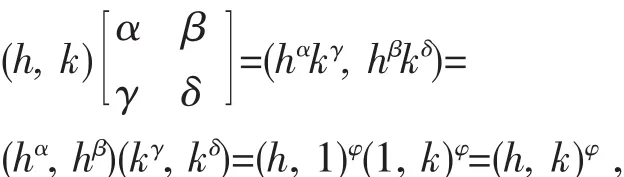
即自同態φ在元素 (h,k)∈G上的取值在形式上與通常的矩陣乘法運算相一致。事實上,直積的任意兩個自同態的合成在形式上也符合通常的矩陣乘法運算規律。

引理2[1]設G=H×K為群的直積,任取G的兩個自同態

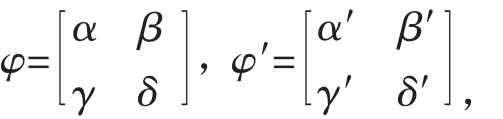
則自同態的合成 φφ′∶→ (gφ)φ′的矩陣表示為

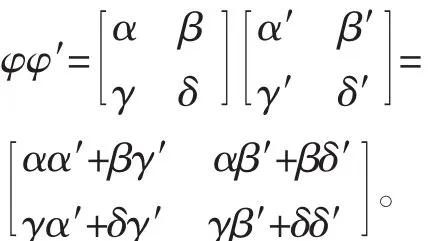
進而,為了描述直積G=H×K的自同構,在文獻[1]中考慮了四個特殊形狀的映射矩陣:

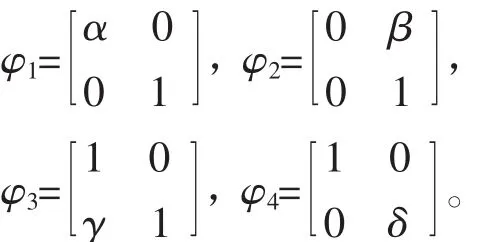
引理3按上述四個映射φ1∶G→G的矩陣記法,則

(1)φ1為G的自同構當且僅當α∈AutH,

(2)φ2為G的自同構當且僅當β∈Hom(H,Z(K)),

(3)φ3為G的自同構當且僅當β∈Hom(K,Z(H)),

(4)φ4為G的自同構當且僅當γ∈AutK。

證明根據引理1及引理2中的自同態矩陣表示及其乘法運算規則直接驗證。

為了使用本文的主定理推導文獻[1]中定理3.2和定理3.6,我們需要引用在文獻[1]中§2預備結果的一個引理。方便起見,我們引入一個記號:如果X為群,θ∈EndX為X的一個自同態,則記CX(θ)={x∈X｜xθ=x}為自同態θ在群X中的所有不動點構成的集合,顯然為X的一個子群,稱之為θ在X中的不動點子群。

引理4設G=H×K為有限群的直積,任取φ∈AutG,設φ和φ′的矩陣表示分別為

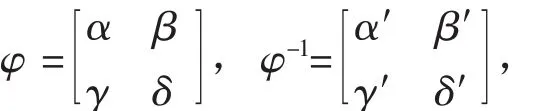
如果H和K沒有同構的直因子,則下述結論成立:

(1)βγ′∈EndH，且 GH(βγ′)=1,

(2)γβ′∈EndK，且 GK(γβ′)=1。

證明此即文獻[1]中推論2.8的一個等價表述。

2 主要結果及證明

設H和K為任意兩個有限群,令G=H×K為直積。方便起見,我們往往約定H和K均為G的子群,即將該直積視為內直積。定義

按上一節預備知識的說明,根據自同構的矩陣表示,我們已知上述四個群均為AutG的子群,并且還滿足性質:AD=A×D可正規化B和C。方便起見,我們稱這四個群A，B，C，D為與群直積G=H×K相伴的自同構群。

定理1設G=H×K為兩個有限群的直積,相伴的自同構群A，B，C，D如上定義,則AutG=ABCD當且僅當對每個φ∈AutG,均有Hφ∩K=1。

證明(充分性)任取 φ∈AutG,按假設 Hφ∩K=1。設φ的矩陣表示為

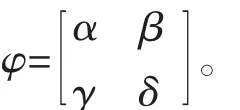
因為φ也是G的自同態,故上述映射α,β,γ,δ也滿足引理1中的六個條件。特別地,這四個映射均為群同態。我們將分以下幾步完成充分性的證明。

(1)驗證α∈AutH:因為α為H的一個自同態,故只需驗證α為雙射即可。任取h∈H,如果hα=1，按映射矩陣的定義, 則 hφ=hαhβ=hβ∈K, 即 hφ∈Hφ∩K。故從所給的條件Hφ∩K=1得到hφ=1。但φ為自同構,只有h=1,表明α為單同態。又因為H為有限群,故α也是雙射,從而為H的一個自同構。

(2)驗證δ∈AutK:如果某個k∈K滿足kδ=1,則按 φ 的矩陣表示之定義得到 kφ=kγkδ=kγ∈H,即kφ∈H∩Kφ。 根據所給的條件:對每個 ψ∈AutG,均有 Hψ∩K=1。現在令 ψ=φ-1, 則 Hφ-1∩K=1,兩邊作用φ得到H∩Kφ=1,據此推出kφ=1。但φ為G的自同構,迫使k=1。 按上述說明,δ為K的自同態,故亦為單同態。同樣從K為有限群推出δ也是K的一個自同構。

(3)驗證Imβ?Z(K):根據(2)可知δ為K的自同構,故其像Imδ=K。但從引理1可知 [Imβ,Imδ]=1,表明Imβ可中心化K的每個元素,即Imβ?Z(K)。

(4)構造自同構ψ∈B:由(1)可知α∈AutH,故可令 β′=α-1β,即 β=αβ′。 因為 β 為群同態, 故 β ∶H→K也是一個群同態。由(3)可知Imβ?Z(K),所以β′∈Hom(K,Z(H))。但后者構成一個加法群,故β的負元-β∈Hom(K,Z(H))。令

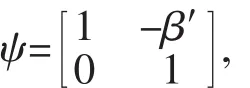
根據引理3,(2)可知ψ為G的一個自同構,顯然ψ∈B。再根據引理2,按矩陣的形式乘積可計算出自同構的合成φψ之矩陣表示:

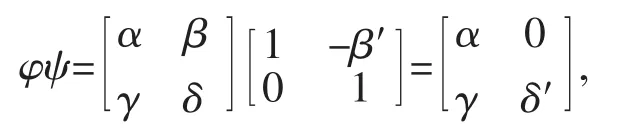
其中記 δ′=γ(-β′)+δ=-γβ′+δ。

(5)驗證δ′∈AutK:因為φψ也是G的自同態,故其矩陣表示中的映射仍滿足引理1中的六個條件,特別地,從引理1,(4)推出δ′∈EndK為K的自同態。任取 k∈Kerδ′，即 kδ-1=1,則 kφψ=krkδ′=kγ∈H。但 hφψ=hα∈H,?h∈H,表明 Hφψ∈H, 故 k∈H(φψ)-1=H。又因為H∩K=1，只有k=1,即δ′為單同態。同樣從K為有限群又可推出δ′為K的自同構。

(6)構造自同構ρ∈C:仍從(1)可知α∈AutH,故可令 γ′=γα-1，即 γ=γ′α。再用引理 1,(5) 可知[H,Imγ]=[Imα,Imγ]=1，從而 Imγ?Z(H),故 γ∈Hom(K,Z(H))。顯然 Z(H)α=Z(H),所以 γ′=γα-1∈Hom(K,Z(H))。熟知后者為加法群,故 γ′的負元-γ′∈Hom(K,Z(H))。設

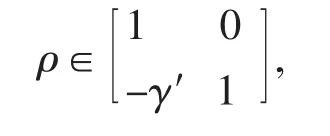
則從引理3,(3)可知ρ也是G的一個自同構,按定義顯然ρ∈C。

(7)驗證AutG=ABCD:仍按引理2中的形式矩陣乘法運算得到

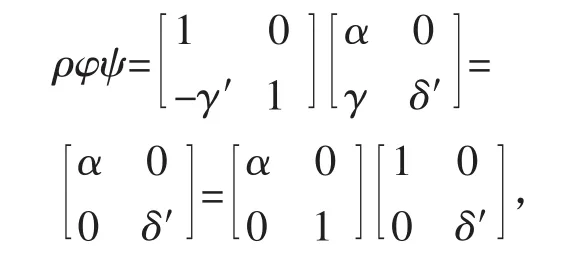
其中最后一個等式成立是因為(1)和(5)分別保證了α∈AutH和δ′∈AutK。再按自同構群A和D的定義可知 ρφψ∈AD。 但從(4)和(6)分別看出 φ∈B和 ρ∈C,而B和C均為AutG的子群,所以φ∈ρ-1(AD)ψ-1?C(AD)B。再由φ∈AutG的任意性,推出AutG=CADB。注意到AD=A×D可正規化B和C,所以(AD)B為子群,故從C(ADB)=AutG為群又可推出C(ADB)=(ADB)C。顯然從D可正規化B和C推出DB=BD且DC=CD,最終得到需證的AutG=ABCD。

(必要性)如果AutG=ABCD,按上段同樣的理由,從AD=A×D正規化B和C可推出AutG=C(AD)B。任取φ∈AutG,按A,B,C,D的定義,可設

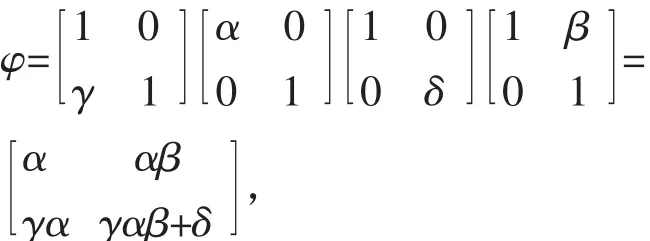
此即自同構φ的矩陣表示,其中

任取k∈Hφ∩K,則可令k=hφ,其中h∈H。 按φ 的矩陣表示之含義,可知 hαhαβ=hφ=k∈K。但 hαβ=(hα)β∈Imβ?K，迫使 hα∈H∩K=1，亦即 hα=1。根據自同構群A中的元素描述,可知α為H的自同構,又可推出h=1,從而k=hφ=1,表明Hφ∩K=1。證畢。

使用自同構的矩陣表示,可得定理1的另一個等價形式:

定理1′ 設G=H×K為兩個有限群的直積,則AutG=ABCD當且僅當對任意

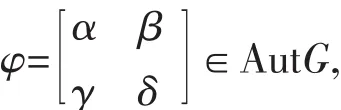
均有α∈AutH,或均有δ∈AutK。

證明 任取hφ∈Hφ∩K,其中h∈H,則按 φ 的矩陣表示之含義,可知 hφ=hαhβ, 所以 hα∈H∩K=1，即k∈Kerα。據此推出 Hφ∩K?(Kerα)φ，不難看出該推導過程可逆,即反包含關系也成立,表明Hφ∩K?(Kerα)φ。所以 Hφ∩K=1,當且僅當 α 為單同態, 后者又等價于α為自同構,使用定理1即得所證。

同理,任取 k∈Hφ-1∩K, 按定義有 kφ=kγkδ∈H。但 kγ∈H, 故 kδ∈H,即 kγ∈H∩K=1,等價于 k∈Kerδ。 所以 Hφ-1∩K?Kerδ,同樣可看出該推理過程可逆,故反包含關系也成立,據此得到Hφ-1∩K?Kerδ。所以 Hφ-1∩K=1當且僅當δ為單同態,又當且僅當δ為自同構。注意到φ-1可隨φ取遍AutG的所有元素,再使用定理1即可完成所證。證畢。

使用文獻[1]中的一個引理(即本文引理4)可從定理1′直接推出文獻[1]中定理3.2和定理3.6:

推論1設G=H×K為兩個有限群的直積,如果H和K沒有同構的直因子,則AutG=ABCD。

證明任取φ∈AutG,設φ和φ-1的矩陣表示分別為

因為 φφ-1=1的矩陣表示顯然為恒等矩陣,故有αα′+βγ′=1。

根據引理1可知α為H的自同態。如果h∈H滿足 hα=1,則從 αα′+βγ′=1 推出 h=hαα′+βγ′=hαα′hβγ′=hβγ′表明 h∈CH(βγ′)為不動點。使用引理 4,(1)得到 h=1,故α為單同態。但H為有限群,所以α也是H的自同構。使用定理1′即得所需結論,證畢。

下述為定理1的直接推論:

推論2設G=H×K為兩個有限群的直積,如果H或K為G的特征子群,則AutG=ABCD。

例如,當G=H×K,K為交換群且Z(H)=1時,則Z(G)=Z(H)×Z(K)=K,表明K即為G的一個特征子群,此時可應用推論2得到AutG=ABCD。注意到C?Hom(K,Z(H))=1,而AD可正規化B,根據A,B,D的結構又可得

[1]Bidwll J N S,Curran M J,Mccaughan D J.Automorphisms of direct products of finite groups[J].Arch Math,2006,86(6):481-489.

[2]Robinson D J S.A Course in the Theory of Groups[M].New York:Heidelberg-Berlin,Springer-Verlag,1982.

[3]徐明曜.有限群導引(上冊)[M].北京:科學出版社,1999.

[4]Curran M J.Direct products with abelian automorphism groups[J].Communications in Algebra,2007,35:389-397.