位移差公式的辨析
白紅艷
(寶安高級中學 廣東深圳 518128)
1 位移差公式
做勻變速直線運動的物體,在相鄰相等時間間隔內的位移差表示為
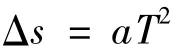
常見證明方法是第一個時間T內的位移
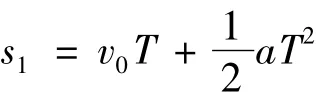
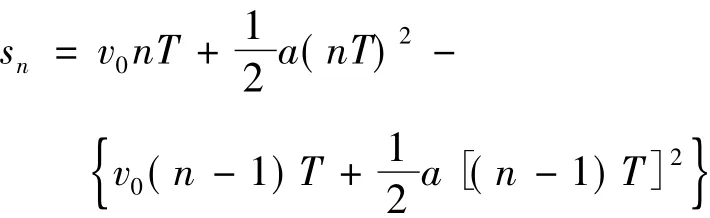
位移差 Δs=sm-sn=(m-n)aT
2 對公式成立條件的誤解
在證明及應用公式的時候,我們潛意識的認為這里的m,n都是取整數,并且我們取的時間間隔通常是獨立、不重合的時間間隔.
大家是否考慮過下面的問題.
(1)當m,n有重合的時候,推論是否成立?
(2)如果想利用推論得到的m,n值,去求物體運動的總時間,當得到的m,n值是分數時,這個推論是否還成立?
3 對公式成立條件的討論
在勻變速直線運動中,位移
第二個時間T內的位移

在相鄰相等時間間隔內的位移差Δs=s2-s1=aT2
做勻變速直線運動的物體,在第m個時間T內和第n個時間T內(m >n)的位移是

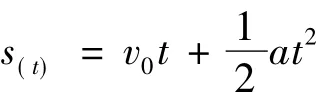
設 s(T1),s(T2),s(T1+T2)的起始點相同,則易證

討論:
當T1=T2=T時就是文中的Δs=aT2,即所取的時間間隔就是T.
當 T1=T,T2=T - Δt時,立即可得

即所取時間間隔T有重合的時候.
結論:
當第m個T與第n個T所取的時間有重合的時候

上面表達形式與沒有重合時
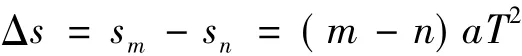
其表達形式實質上是一致的,即推論Δs=sm-sn=(m-n)aT2的形式仍然正確.
4 公式應用舉例
【例題】一個物體從某一高度做自由落體運動,已知它第1 s內的位移為它最后1 s內位移的一半,g取10 m/s2.求物體開始下落時距離地面的高度.
解:根據Δs=sm-sn=(m -n)aT2
將題給條件代入,有

由(1)、(2)、(3) 式解得m=1.5說明:原本時間間隔是T=1 s,但是解得的m值不是T=1 s的整數倍,而是,說明題中的第1 s和最后1 s實際上是有重合的.如果沒有重合的話,m應該是2T,3T等說明總的時間不足2T.
我們可以通過系數關系,計算出重合的部分時間Δt是多少.還可以知道總的時間是,即 1.5 s.


綜上,對Δs=aT2和sm-sn=(m-n)aT2成立條件的正確理解應該是包含兩個時間間隔相等且重合的情況,也包含m,n不能取整數的情況

