虛擬環(huán)境下的直線度公差表現(xiàn)形式的研究

韓志遠，王彤宇，程少東

(1.長春理工大學 機電工程學院，長春 130022；2.吉林油田公司，松原，131200)

公差是CAD/CAM集成中必不可少的信息，也是設(shè)計中的研究熱點之一[1-3]。現(xiàn)有的繪圖軟件都是實體造型器，它僅僅提供對實際物體精確的數(shù)學表示，而不能表示對后續(xù)裝配工作的全部信息，如公差信息、材料及技術(shù)要求等，不能實現(xiàn)有效的集成。在實際的裝配中，裝配對產(chǎn)品質(zhì)量的優(yōu)劣和性能的好壞起決定性作用，也對產(chǎn)品價格有重要的影響作用。國際生產(chǎn)工程學認定公差信息是產(chǎn)品裝配最重要的信息。

1 直線度公差數(shù)學建模的理論基礎(chǔ)

在實際加工中，誤差的來源可分成內(nèi)部誤差和外部誤差兩種。外部誤差主要是指影響機床加工精度的周圍環(huán)境的溫度、臨近設(shè)備的振動、電網(wǎng)電壓波動、空氣濕度與污染、操作者的干預(yù)等；內(nèi)部誤差主要是指機床加工系統(tǒng)內(nèi)部因素引起的誤差，包括加工原理誤差、幾何誤差、受力變形、熱變形、刀具磨損、切削力及其力矩、摩擦力、振動等。其中影響直線度公差比較大的是切削力、微振動和系統(tǒng)誤差中的機床和加工誤差，這幾項的總和幾乎占到90%以上。因此要在虛擬現(xiàn)實中考慮諸多主要因素，忽略一些次要因素。

直線度公差模型的研究成果主要集中在以下五個方面：

1.漂移模型其數(shù)學表達式為：

T=(S，{Fi}，{Aij})式中，S為所需添加公差的實體，{Fi}為該名義實體邊界，{Aij}是公差要求；

2.基于幾何約束變動的參數(shù)矢量化數(shù)學模型其數(shù)學表達式為：

式中，x為零件的參數(shù)矢量，f為公差函數(shù)，L、U為公差域的上下界；

4.基于漂移和自由度的數(shù)學模型；

5.基于數(shù)學定義和自由度變動的數(shù)學模型；以上五種建模方法都各有其優(yōu)缺點[4]，通過最基礎(chǔ)的約束關(guān)系建立數(shù)學模型。

通過深入研究尺寸公差與形狀公差之間的關(guān)系以及形狀公差的本質(zhì)，可以找到對形狀公差的唯一限制。即：在要素的整個包圍盒范圍內(nèi)，形狀公差域與尺寸域的交集不能為空集。由此確定直線度公差在尺寸公差域內(nèi)的方向和位置[5]。

在給定平面內(nèi)，公差帶是距離為公差值t的兩平行直線之間的區(qū)域即為直線度。直線共有四個自由度：x，y，， ，對于長為 的直線，在自由度方向上給定一變動 dx，dy，dx，dy則其數(shù)學模型變動如下：

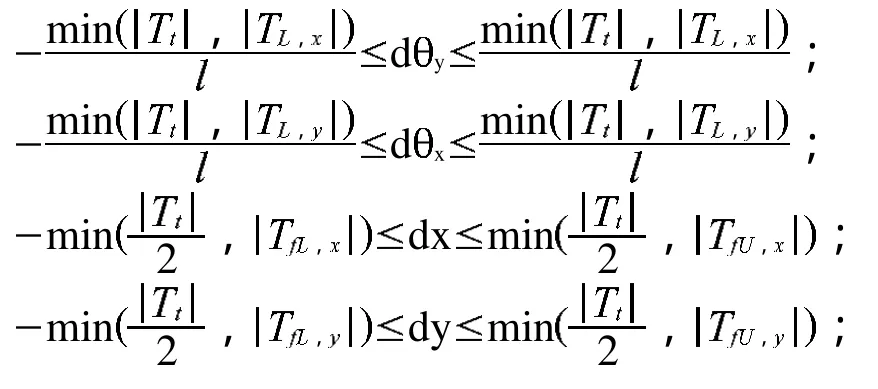
通過在虛擬環(huán)境下，模擬機床加工的真實切削過程，并考慮到諸多因素的影響，通過提取數(shù)據(jù)和分析數(shù)據(jù)，繪制出與實際真實直線度比較接近的曲線，隨機反映出直線度的變化。

2 各因素影響誤差的仿真

2.1 機床微振動對直線度的影響

ADAMS是以計算機多體系統(tǒng)動力學為基礎(chǔ)，包含多個專業(yè)模塊和專業(yè)領(lǐng)域的虛擬樣機開發(fā)系統(tǒng)軟件，利用它可以建立起復雜機械系統(tǒng)的運動學和動力學模型，其模型可以是剛性體，也可以是柔性體，以及剛?cè)峄旌夏Ｐ汀Ｈ绻诋a(chǎn)品的概念設(shè)計階段就采用ADAMS進行輔助分析，就可以在建造真實的物理樣機之前，對產(chǎn)品進行各種性能的測試，達到縮短開發(fā)周期、降低開發(fā)成本的目的。

機床的微振動主要是由主軸系統(tǒng)的不對稱和聯(lián)軸器偏差以及機床本身的整體設(shè)計的不同引起的，不同的機床，它的材料、結(jié)構(gòu)和裝配誤差都不相同，所引起的微振動的大小也不相同，不過這些都會通過加工刀具反映到被加工件上，我們可以通過分析被加工件的公差變化，實施振動誤差補償。利用ADAMS軟件的強大功能，在虛擬環(huán)境下，考慮到機床微振動的影響，分析出機床本身的振動，對加工件直線度公差的影響。

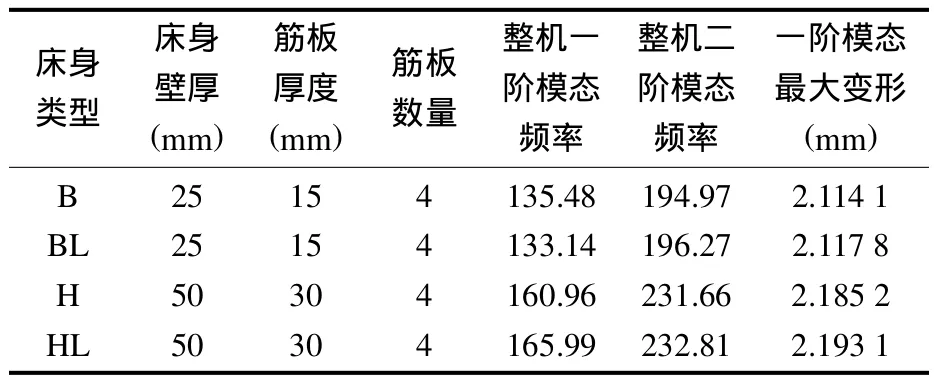
表1 數(shù)據(jù)分析Tab.1 Data analysis

經(jīng)過振動模態(tài)分析，可以得出一些相關(guān)的頻率數(shù)據(jù)。分析數(shù)據(jù)得出只有在機床本身的頻率遠遠大于或遠遠小于機床電機的頻率，才可以減少共振對加工的影響。通過機床本身的頻率與機床電機頻率的比較，當兩者相距較大的時候，對直線度公差的影響也會相對較小。在有嚴格公差要求時，為選擇不同的機床加工做出了理論依據(jù)。

2.2 機床系統(tǒng)誤差對直線度的影響

綜合機床的加工誤差，在機床工作過程中，任意單元的誤差也是多種誤差因素作用的結(jié)果，因此本質(zhì)上來說每一項誤差都是各種因素引起的綜合誤差。可以用公式表示如下：

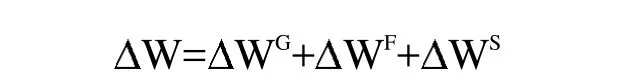
2.3 Deform虛擬高速車削加工仿真

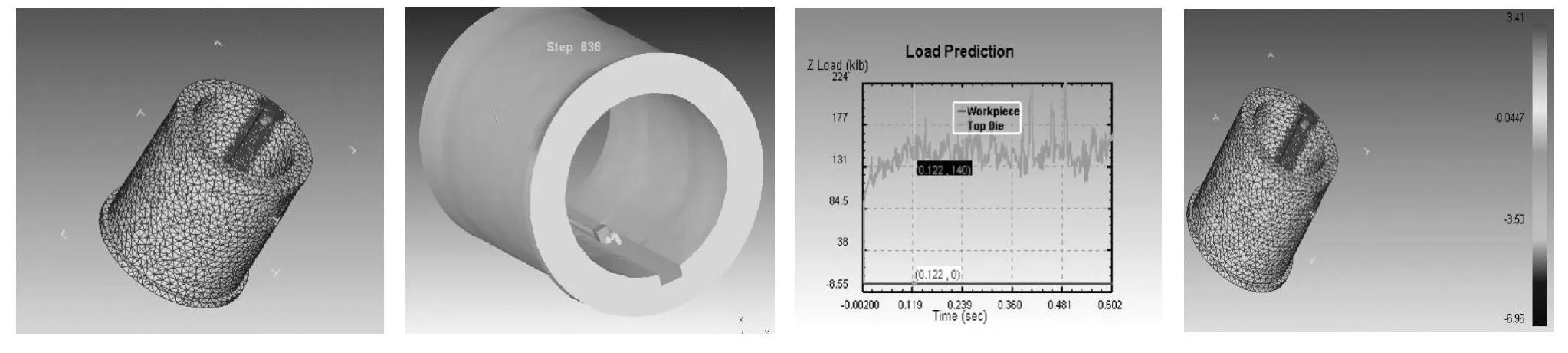
圖1 虛擬切削過程Fig.1 The virtual cutting process

鍵槽的加工深度為 5mm，通過選擇簡單刃刀具、作用力的激勵。選擇了普通車床CA6140加工鍵槽，并對系統(tǒng)誤差進行了適當?shù)难a償，補償系數(shù)為0.05。綜合了上述影響因素，利用Deform軟件的強大功能，在虛擬環(huán)境下，虛擬仿真機床切削過程。對鍵槽進行網(wǎng)格化，對切削過程的力進行分析和繪制，對鍵槽的實際變形通過右側(cè)顏色對比顯示。刀具材料：wc，工件材料：AISI-1045，車速：105m/min。

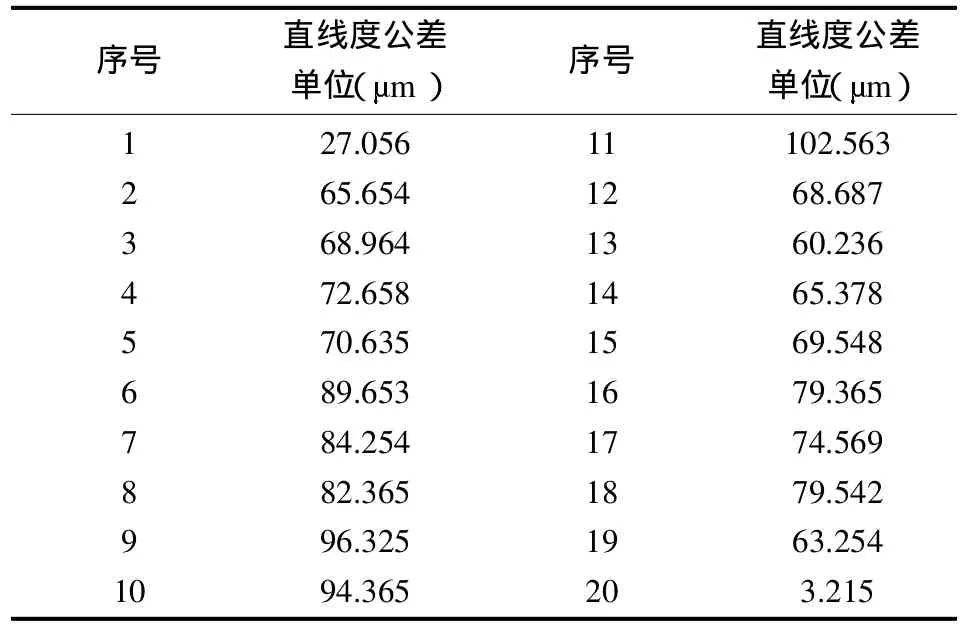
表2 輪廓誤差的部分數(shù)據(jù)Tab.2 Outlines some of the data error

圖1從對切削力的描述中可以看出力的變化是圍繞著一個中心線上下波動，整個切削過程都是隨機波動的，但也有軌跡可循。當把鼠標點在鍵槽已加工處，可以從右側(cè)的顏色標注中讀出鍵槽的變形值。選取鍵槽面提取隨機直線度變化數(shù)據(jù)，通過數(shù)據(jù)分析，可以很清楚地看到在綜合了上述影響因素的條件下，隨機直線度公差的變化情況如上表。

3 誤差的綜合和綜合誤差的仿真

通過以上誤差分析，綜合主要誤差的影響，對分析圖表進行加權(quán)計算和網(wǎng)格化對比與分析。標注鍵槽直線度公差為0.1加工材料，提取原始數(shù)據(jù)。

數(shù)學上，在數(shù)據(jù)點的最小誤差平方和，且所用的曲線限定為多項式時，那么曲線擬合是相當簡捷的，稱為多項式的最小二乘曲線擬合。為了將曲線擬合解與數(shù)據(jù)點比較，讓我們把二者都繪成圖。x坐標為時間t/s，y坐標為輪廓誤差值。為了看清楚實際直線度的變化，將坐標軸擴大1000倍，具體的應(yīng)用程序如圖2所示。

圖2 數(shù)據(jù)處理的應(yīng)用程序Fig.2 Data processing applications

圖3 公差描繪的隨機曲線Fig.3 Depicts the random curve tolerance

在虛擬加工中，隨機直線度會重復著上圖的曲線，我們可以很清楚看到直線度的變化。以上結(jié)果可提取主要參數(shù)，通過編程集中到繪圖軟件上，使得標注成為動態(tài)變化。下一步研究將主要是編程，通過人工選擇車床的加工參數(shù)，系統(tǒng)會自動生成動態(tài)的直線度公差曲線，為后續(xù)裝配提供信息指導。

4 結(jié)論

公差是繪圖軟件集成的必要信息之一。目前公差信息很不完善，對加工的指導意義不是很大，針對這一點，給出了實際加工中，直線度的隨機變化，隨著加工條件的變化，直線度也會隨之變化的，文中只是給出一個描述，作為參考性。這對隨機公差的變化有著十分重要的意義。

[1]劉玉生.基于自由度變動的直線度公差數(shù)學模型[J].工程設(shè)計學報，2002，9(11)：27-30.

[2]Bjorke.Commputer Aided Tolerancing[M].New York：ASME Press，1989，13(2)：13-16.

[3]Shah JJ.D imension and tolerance modeling and transformations in feature based design and manufacturing[J].Jourmal of Intellignt M anufacturing，1998，9(5)：475-488.

[4]劉玉生，楊將新，吳昭同，等.CAD系統(tǒng)中公差信息建模技術(shù)綜述[J].計算機輔助設(shè)計與圖形學學報，2001，13(11)：1048-1054.

[5]劉玉生.基于數(shù)學定義的平面尺寸和形位公差建模與表示技術(shù)的研究[J].浙江大學學報，2000，37(9)：12-16.