深吃水半潛式平臺垂蕩響應數值分析

朱航，歐進萍

(1.船舶工藝研究所，上海 200032;2.哈爾濱工業(yè)大學 土木工程學院，黑龍江 哈爾濱 150090;3.大連理工大學 土木水利學院，遼寧 大連116023)

半潛式平臺是坐底式平臺和小水線面船概念相結合的結果.由于相對于Spar平臺和TLP平臺而言，半潛式平臺初期投資較少，自20世紀60年代出現以來，半潛式平臺在海洋油氣的勘探開采中得以廣泛的應用［1］.目前，半潛式平臺已發(fā)展至第六代平臺，有著適用工作水深廣，抗風浪能力強，甲板空間大等眾多優(yōu)點.

但是，半潛式平臺的缺點也很明顯.半潛式平臺的垂向運動較大，干樹采油系統(tǒng)不能應用在其上，大大增加了作業(yè)成本與維護成本［2］.如何減小平臺的垂蕩響應，成為國內外學者研究的熱點［3］，深吃水半潛式平臺結構的概念也由此問世.深吃水半潛式平臺的吃水深度往往在40 m左右，遠大于常規(guī)半潛式平臺的15～25 m吃水.另外，由于吃水較深，深吃水半潛式平臺往往沒有自我航行能力，平臺的浮體常采用四方環(huán)形設計，這樣可以更好地保證平臺的穩(wěn)定性.

吃水深度的增加很好地抑制了平臺的垂蕩響應，Bindingsb［4］的研究結果表明，與常規(guī)半潛式鉆井平臺相比，深吃水半潛式平臺的垂蕩及縱搖RAO可以減小50%左右.但是該作者在文中只說明了平臺的吃水深度與排水量參數，且文中主要聚焦于立管的性能問題，對平臺主體部分的研究不夠.Youngpyo hong［5］等學者也研究了深吃水半潛式平臺的浮體在浪、流聯合作用下的渦激振動，他們的計算結果表明，浮體的渦激振動與波浪和海流的速度有著很大的關系.

J.Halkyard［6］對深吃水半潛式平臺的結構進行了更大的改進，提出了DPS系列平臺，其特點是在深吃水半潛式平臺上增加了可收放的垂蕩板，令平臺的垂蕩響應進一步減小.嚴格地說，DPS系列平臺已經脫離了半潛式平臺的特點，其結構原理和特點更與Truss-spar平臺更為接近.DPS系列平臺的垂蕩板是縮進式的，可以收起至平臺主體所圍成的空間中，解決了平臺運輸方面的困難.

鑒于DPS系列的種種優(yōu)點(附加垂蕩板、縮進變形等)，其結構形式也許將成為未來深水半潛式平臺的主流，下面針對DPS 2001-4平臺，分析垂蕩板對平臺垂蕩響應的影響，并對平臺主體吃水深度的變化對平臺垂蕩響應所造成的影響進行研究，以更深入地對半潛式平臺的結構形式進行改進.

1 DPS-4平臺尺寸參數及錨泊系統(tǒng)參數

1.1 DPS 2001-4平臺尺寸參數

圖1為DPS 2001－4平臺的結構示意圖.該平臺的設計水深為1 000 m，其水下結構可以包括主體水下結構與垂蕩板2部分(連接桁架體積相比二者很小，因此不考慮).主體水下結構可以分為立柱和浮體:立柱共 4個，其截面尺寸為12.20 m× 12.20 m，柱中心的間距為48.40 m，浮體的寬度和深度為12.20 m;垂蕩底板為3.05 m厚度的軟倉，截面尺寸61.00 m×61.00 m，垂蕩板中心處設置12.20 m×12.20 m的方孔以保證立管系統(tǒng)的順利通過.平臺主體吃水為61.00 m，垂蕩板底部水深為97.60 m，圖2為平臺水下結構的數值模型.

圖1 DPS 2001-4平臺Fig.1 DPS 2001-4 deep draft semi-submersible platform

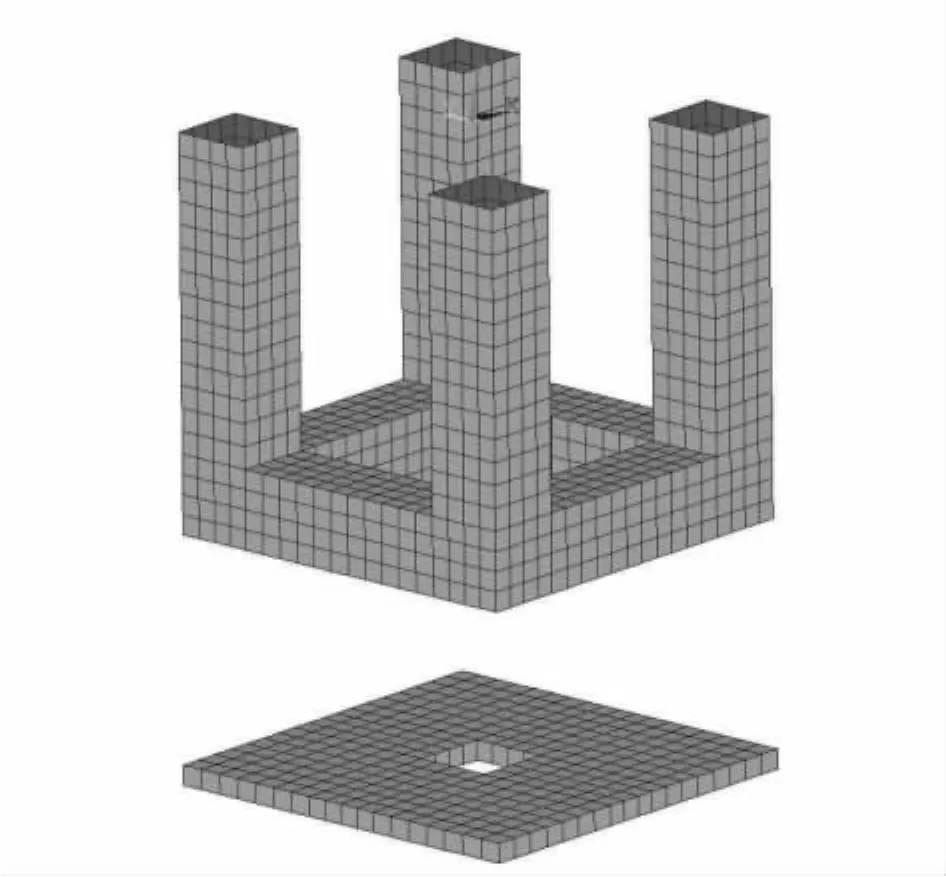
圖2 平臺水下結構數值模型Fig.2 Numerical model of DPS 2001-4 platform

1.2 錨泊系統(tǒng)參數

平臺的錨泊系統(tǒng)由16根錨鏈組成，其中每4根錨鏈為一組，各分布于平臺的一角，同組中相鄰錨鏈的水平投影線夾角為5°，單根錨鏈為鏈－纜－鏈結構，3種材料的參數如表1.每根錨鏈的頂端與水平面的夾角為60.8°.

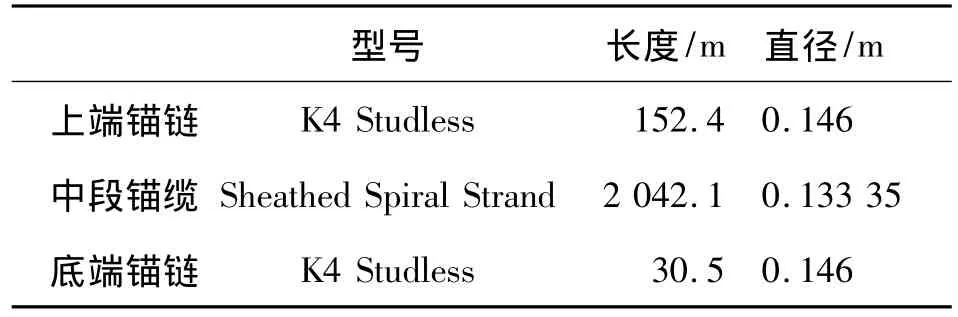
表1 錨鏈參數Table 1 Parameters of a mooring line

2 數值計算方法

DPS2001-4半潛式平臺的垂蕩運動方程可以表示為

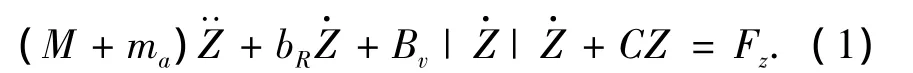
式中:M、ma和Br分別為平臺質量、垂向附加質量和輻射阻尼，C為垂向剛度，Z為平臺的垂向位移，Fz為平臺的垂向激振力，它與固定平臺上的波浪力相同.

2.1 垂向剛度計算

平臺的垂向剛度包括靜水回復剛度C1與錨泊系統(tǒng)的垂向回復剛度C2兩部分，靜水回復剛度C1與平臺的水線面積S1有關，C1=Sγ，γ為海水容重.

錨泊系統(tǒng)的垂向剛度C2可采用分段外推－校正法［7］求解，其計算原理如下:

1)已知海水深度、錨鏈頂端與水平面的夾角θTop;

2)把錨鏈劃分成若干個微段;

3)假設錨鏈頂端的拉力TTop已知;

4)計算每個微段上的重力和浮力;

5)建立微段的靜力平衡方程(圖3).

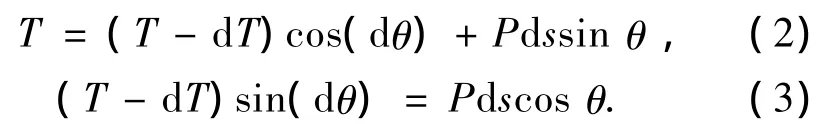
式中:T為微段頂端受到的拉力，P為單位長度的錨鏈受到的重力與浮力的合力，θ為微段頂端切線與水平方向的夾角，ds為微段的長度，dT和dθ分別為拉力和角度的變化量.考慮錨鏈微段的幾何關系，有

其中，ε=T/(EA)為單位長度的錨鏈的伸長量，E、A分別為錨鏈的彈性模量和橫截面積.通過式(4)和式(5)可求出錨鏈上任意一點的坐標值(x，z):

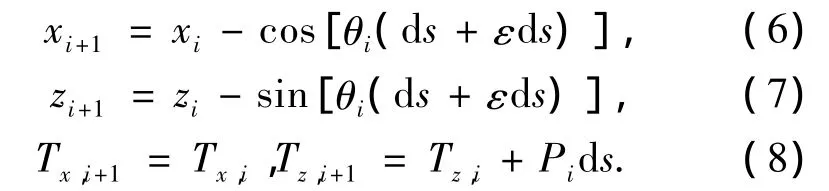
式(8)可得出下一段的水平力與豎直力，用于接下來的計算.

圖3 錨鏈微段示意圖Fig.3 Segment of the mooring line

最后驗證錨鏈底端坐標zend的水深邊界條件:如滿足一定的精度，計算結束;如不滿足，則返回3)，調整錨鏈頂端拉力TTop值的大小，重復計算.

在確定了TTop值的大小之后，錨泊系統(tǒng)頂端在豎直方向的拉力TTop，V

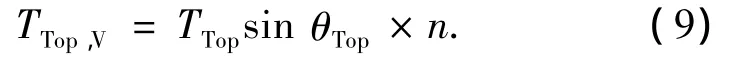
其中，n為錨泊系統(tǒng)中錨鏈的根數.

通過以上方法，得到錨鏈頂端拉力及其在豎直方向的分量.由于錨鏈頂端與水平面夾角為60.8°，可以確定錨鏈豎向拉力隨平臺垂蕩響應的變化如圖4.

圖4的計算結果表明，平臺錨泊系統(tǒng)的垂向剛度為非線性數值，其最大值為302 kN/m，與平臺的靜水垂向回復剛度比較，有

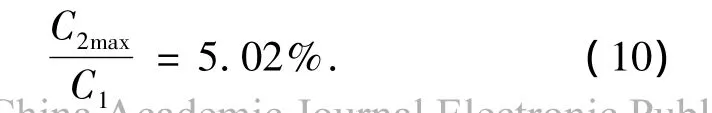
式(10)的計算結果表明:錨泊系統(tǒng)的垂向剛度最大值只有靜水垂向回復剛度的5.02%，遠小于平臺的靜水垂向回復剛度，因此，在平臺的垂蕩響應計算過程中，錨泊系統(tǒng)的垂向剛度將忽略不計.

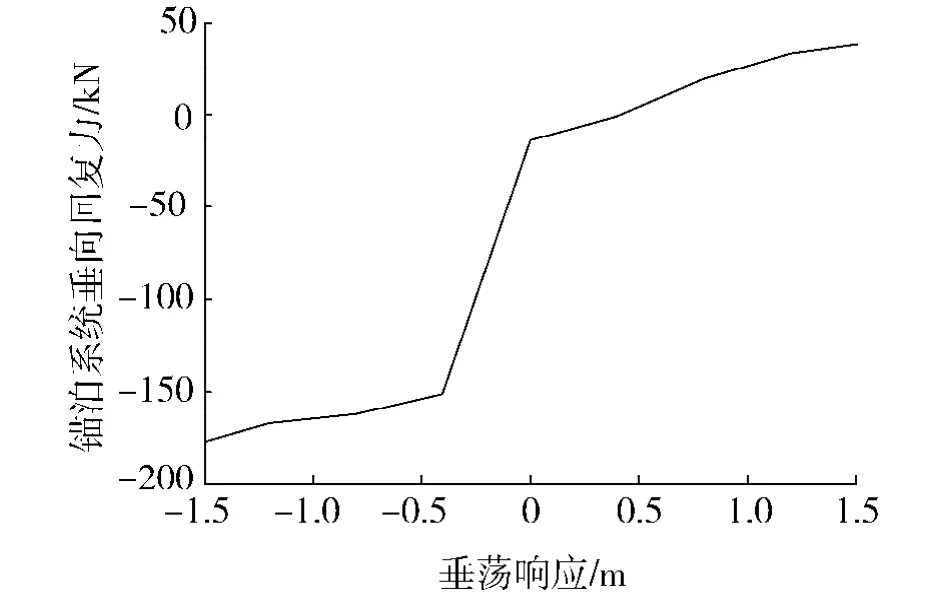
圖4 錨泊系統(tǒng)豎向拉力隨平臺垂蕩響應變化圖Fig.4 Influence of the platform heave motion on the vertical force of the mooring system

2.2 阻尼系數計算

平臺的阻尼可以分為粘滯阻尼與輻射阻尼2部分.粘滯阻尼可以用Bv||表示，Bv=ρSw［8］，Sw為平臺的水下部分在垂向的投影面積(投影重疊部分需疊加，此處不考慮遮蔽效應).而平臺的附加質量和輻射阻尼只與平臺的振動頻率ω相關.

2.3 平臺的垂蕩響應RAO求解

如假設式(1)中粘滯阻尼為0，則可簡化為

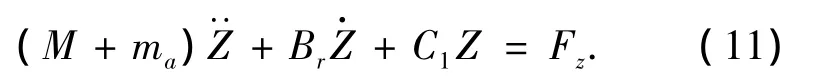
式(11)可以通過頻域邊界元理論［9］，求得平臺各振動頻率下的附加質量ma和輻射阻尼Br.

由于式(11)為簡諧激勵下的響應［10］，在振動頻率為ω時，其穩(wěn)態(tài)解的幅值可表示為

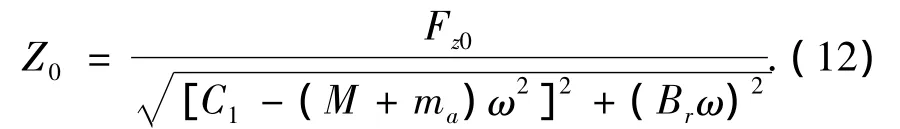
將與振動頻率ω對應的附加質量、輻射阻尼重新代入式(1)，忽略錨泊系統(tǒng)的垂向剛度對平臺垂蕩響應的影響，并假設垂向激振力Fz與垂向位移Z為

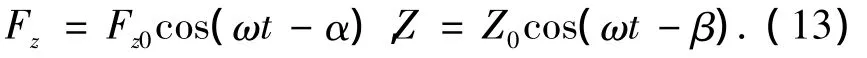
其中，Fz0和Z0分別為力和垂向位移的幅值.式(1)可變?yōu)?/p>

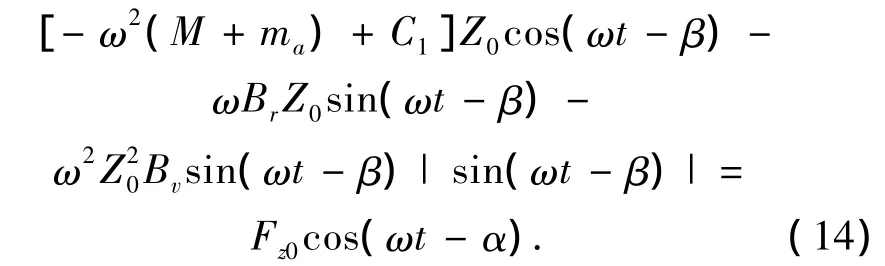
采用傅里葉級數展開，取第1項之后，sin(ωtβ)·|sin(ωt－β)|→8/3πsin(ωt－β)，式(14)可進一步變?yōu)?/p>

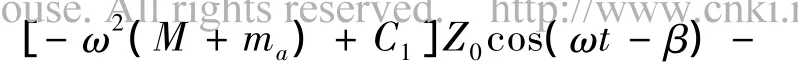
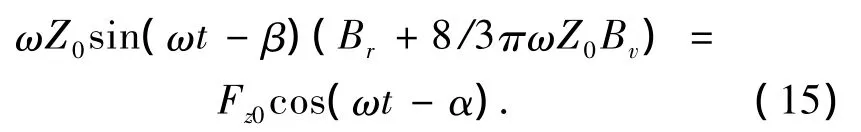
其中，(Br+8/3πωZ0Bv)即系統(tǒng)的等效阻尼，有

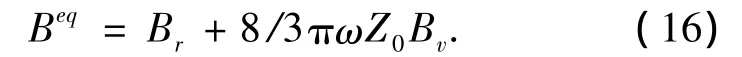
將式(16)代入式(1)，令M0=M+ma，有

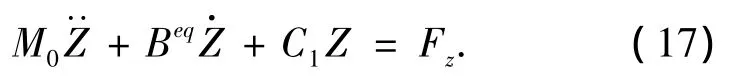
由于Fz與固定平臺上的波浪力相同，其值只與入射波浪與平臺外形相關.與式(11)對比，此處只有系統(tǒng)的阻尼發(fā)生了變化.由于式(17)同樣為簡諧激勵下的響應，在振動頻率同樣為ω時，式(17)穩(wěn)態(tài)解的幅值可表示為

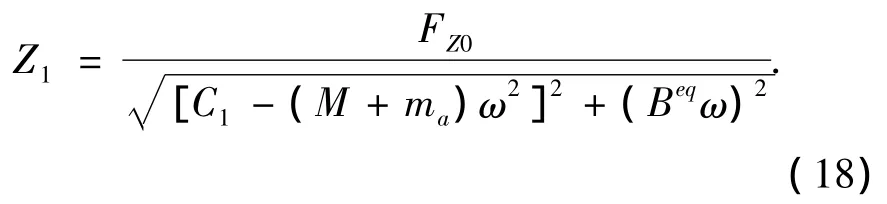
可見，式(16)與式(18)組成了迭代循環(huán)，重復式(16)和式(18)，直至平臺的振幅Zn與系統(tǒng)的等效阻尼滿足計算精度.

這樣，平臺的RAO計算公式可表示為

其中，A為入射波的波幅.

3 計算結果分析

3.1 不同波浪入射角下平臺的垂蕩響應RAO比較

圖5為各波浪入射角下平臺的垂蕩響應RAO結果，考慮平臺的對稱性，取波浪入射角為0°、15°、30°和45°進行分析.圖5的計算結果表明，各波浪入射角下DPS 2004-1平臺的垂蕩響應RAO基本相同.也就是說，波浪入射角對平臺的垂蕩響應RAO基本無影響.因此，下面僅針對0°入射角時平臺的垂蕩響應RAO進行分析.

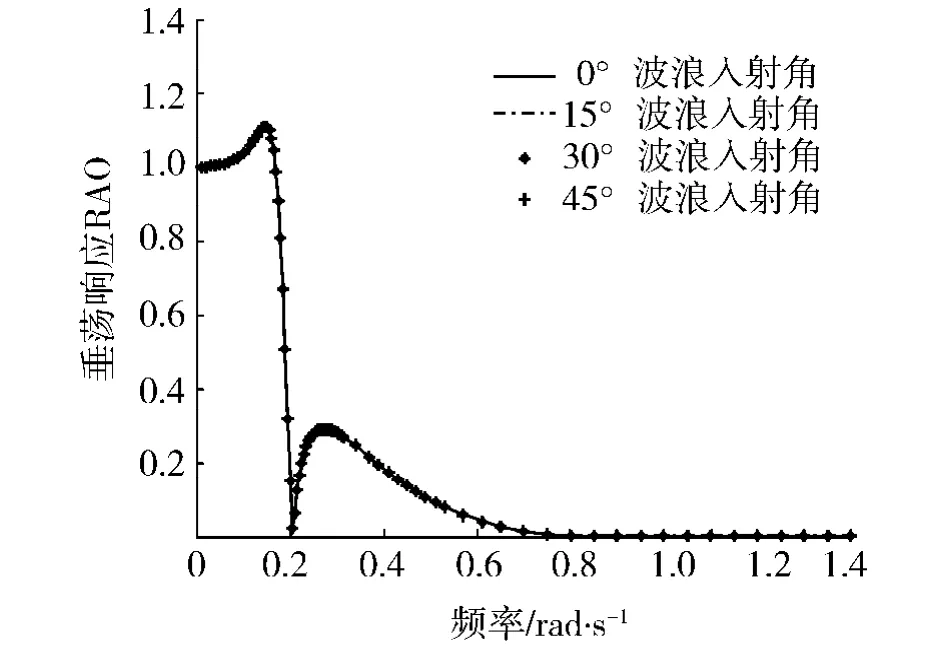
圖5 各波浪入射角下平臺的垂蕩響應RAOFig.5 Platform heave motion RAO in different wave directions

3.2 粘滯阻尼與輻射阻尼比較

下面對粘滯阻尼與輻射阻尼的大小進行比較.圖6為2種阻尼的比較結果.圖6的計算結果表明:在垂蕩響應RAO較大的頻率段，即垂蕩頻率在0～0.4 rad/s頻率范圍內，平臺的粘滯阻尼遠大于輻射阻尼.即使是在其余垂蕩響應RAO較小的振動頻率段，粘滯阻尼也不小于輻射阻尼，這說明，粘滯阻尼在總阻尼中占主要部分.

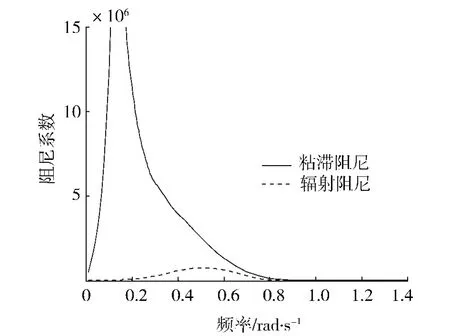
圖6 粘滯阻尼與輻射阻尼的比較Fig.6 Comparison of the viscous damping and radiation damping

3.3 垂蕩板對平臺垂蕩響應RAO的影響

為了研究垂蕩板對平臺垂蕩響應RAO的影響，圖7對比了DPS2001-4平臺與主體相同的常規(guī)深吃水半潛式平臺的垂蕩響應RAO.圖7的計算結果表明，與常規(guī)深吃水半潛式平臺相比，DPS 2001-4平臺的垂蕩響應RAO的自振頻率段進一步遠離了海洋波浪主頻段，達到了更好的垂蕩減振效果.這說明垂蕩板對平臺的垂蕩響應有著很好的抑制作用.

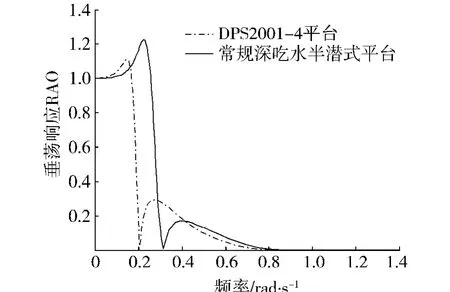
圖7 垂蕩板對平臺響應垂蕩RAO的影響Fig.7 Influence of the heave plate on platform heave motion RAO

3.4 垂蕩板放置深度對平臺垂蕩響應的影響

下面研究垂蕩板放置水深對平臺垂蕩響應的影響.圖8為平臺主體結構相同、垂蕩板水深位置不同時，平臺垂蕩響應RAO的比較.圖8的計算結果表明:隨著垂蕩板放置水深的增加，平臺的垂蕩響應RAO在低頻范圍幅值略有增加，而在波頻范圍幅值則略有下降.總的來說，垂蕩板放置水深對平臺垂蕩響應RAO略有影響，但是影響較小.

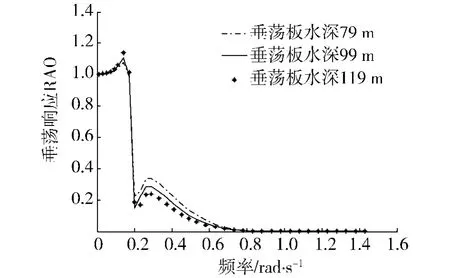
圖8 垂蕩板放置深度對平臺垂蕩響應RAO的影響Fig.8 Influence of the heave plate draft on platform heave motion RAO

為了進一步說明垂蕩板放置深度對平臺垂蕩響應的影響，下面比較各海域百年一遇海況下不同垂蕩板深度時平臺的垂蕩響應極值［11］，海況的選擇如表2.

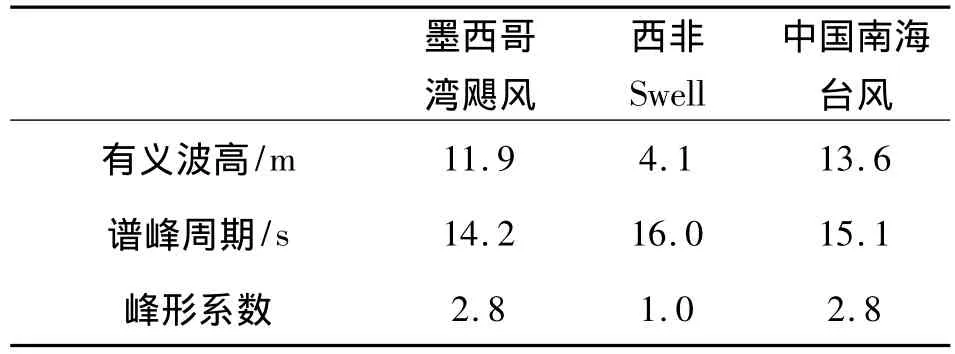
表2 極端海況Table 2 Extreme sea environment

平臺在各海況下的垂蕩響應極值計算方法如下.

首先計算平臺各海況下的垂蕩響應譜.在響應譜分析中，波浪譜選擇為五參數的JONSWAP波能譜，其表達式為［12］

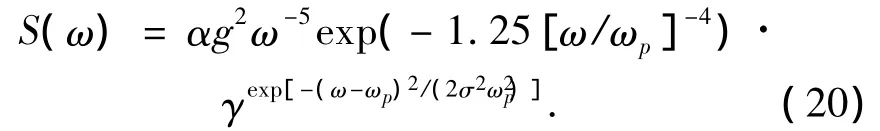
式中:α=5.058［Hs/(Tp)2］2(1－0.287lnγ)為廣義菲利普常數;σ為譜寬常數，當ω＜ωp時，σ=0.07，而當ω＞ωp時，σ=0.09.

平臺的垂蕩響應譜為

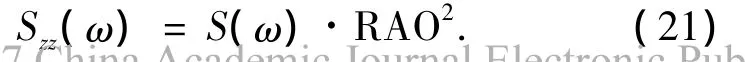
隨機波浪條件下的平臺垂蕩響應極值Xmax的計算公式為［13］

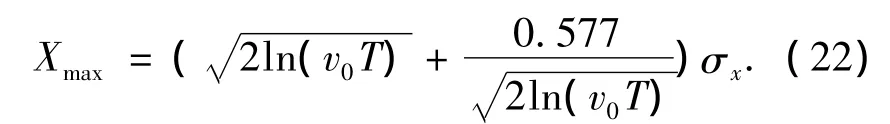
其中，σx和v0分別為平臺垂蕩響應譜Xzz(ω)的標準差和過零率.二者的計算公式分別為

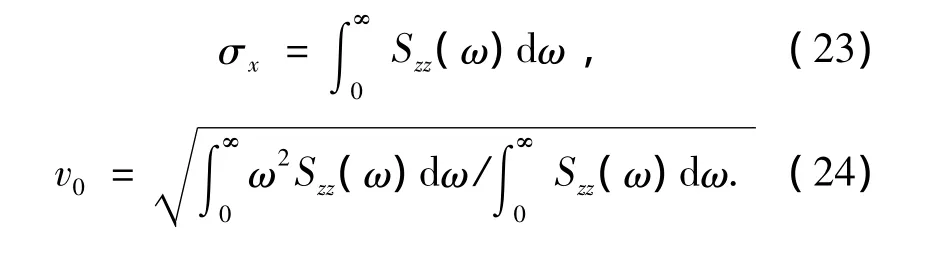
圖9為各海域百年一遇海況下平臺垂蕩響應極值，圖9的計算結果表明:隨著垂蕩板放置水深的增加，平臺在各海況下的垂蕩響應極值逐漸變小，但是這個減小的趨勢逐漸變緩.當垂蕩板吃水深度超過100 m后，下降的趨勢變得更加緩慢，以至于此時中國南海臺風海況和西非Swell海況時平臺的垂蕩響應極值趨于恒定值.這也表明DPS 2001-4平臺的垂蕩板水深位置是合理的.按照DPS 2001-4平臺的垂蕩板吃水水深99 m考慮，平臺在三種海域百年重現期海況下，垂蕩響應極值均不超過2 m，這表示干樹采油系統(tǒng)可以在平臺上使用，這將極大的提高平臺的經濟性.

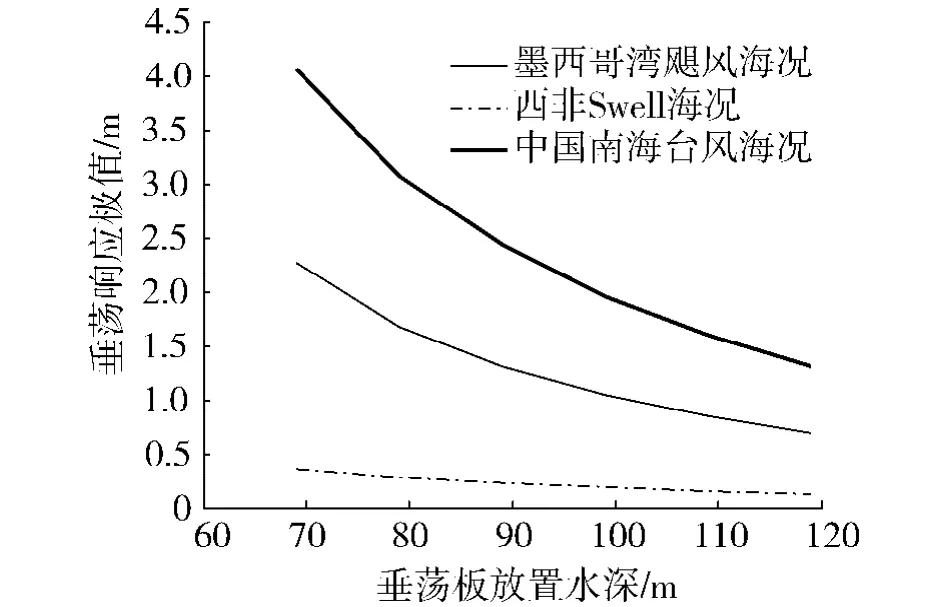
圖9 垂蕩板放置深度對平臺垂蕩極值的影響Fig.9 Influence of the heave plate draft on the platform heave motion extremes

4 結論

將平臺的粘滯阻尼線性化處理，通過數值迭代的方法得到了平臺的垂蕩響應幅值算子(RAO)，并根據得到的幅值算子(RAO)求得了平臺在3種海域下的垂蕩響應極值，得到結論如下:

1)在DPS 2001-4平臺的垂蕩響應計算中，其垂向剛度以平臺的靜水垂向回復剛度為主，而阻尼則以粘滯阻尼為主.

2)垂蕩板對于減小平臺的垂蕩響應有著重要的作用，當垂蕩板下放到指定水深后，與主體相同的常規(guī)深吃水半潛式平臺相比，DPS 2001-4平臺的垂蕩響應自振頻率段進一步遠離了海洋波浪的主要頻率段，達到了更好的垂蕩減振效果.

3)平臺的垂蕩響應極值隨著垂蕩板的放置水深的增加而減小，但是這個減小的趨勢逐漸變緩.垂蕩板的放置水深應根據平臺的性價比而進行合適的選擇.

［1］劉海霞.深海半潛式鉆井平臺的發(fā)展［J］.船舶，2007，6 (3):6-10.

LIU Haixia.Development of deep-sea semi-submersible drilling unit［J］.Ship and Boat，2007，6(3):6-10.

［2］楊立軍，肖龍飛，楊建民.半潛式平臺水動力性能研究［J］.中國海洋平臺，2009，24(1):1-9.

YANG Lijun，XIAO Longfei，YANG Jianmin.Review on the study of hydrodynamics of semi-submersible platforms［J］.China Offshore Platform，2009，24(1):1-9.

［3］CERMELLI C A，RODDIER D G，BUSSO C C.Minifloat:a novel concept of minimal floating platform for marginal field development［C］//Proceedings of the 14th International Offshore and Polar Engineering Conference. Toulon，France，2004:538-545.

［4］BINDINGSBO A U.Deep draft semi-submersible［C］// Proceedings of the 21st International Conference on Offshore Mechanics and Artic Engineering.Oslo，Norway，2002: 651-659.

［5］YONGPYO H，YONGHO C.Vortex-induced motion of a deep-draft semi-submersible in current and waves［C］// Proceedings of the 18th International Offshore and Polar Engineering Conference. Vancouver， Canada， 2008，453-459.

［6］HALKYARD J，CHAO J，ABBOTT P.A deep draft semisubmersible with a retractable heave plate［C］//Offshore Technology Conference Proceedings.Houston，USA，2002.

［7］滕斌，郝春玲.Chebyshew多項式在錨鏈分析中的應用［J］.中國工程科學，2005，7(1):21-26.

TENG Bin，HAO Chunling.Numerical simulation of static behavior of the single anchor cable［J］.Engineering Science，2005，7(1):21-26.

［8］李彬彬，歐進萍.Truss Spar平臺垂蕩響應頻域分析［J］。洋工程，2009，27(1):8-16.

LI Binbin，OU Jinping.Heave response analysis of Truss Spar in frequency domain［J］.The Ocean Engineering，2009，27(1):8-16.

［9］李玉成，滕斌.波浪對海上建筑物的作用［M］.2版.北京:海洋出版社，2002:63-75.

LI Yucheng，TENG Bin.Wave action on maritime structures［M］.2nd ed.Beijing:China Oean Pess，2002:63-75.

［10］胡宗武.工程振動分析基礎［M］.上海:上海交通大學出版社，1999:44-50.

HU Zongwu.Fundamentals of engineering vibration analysis［M］.Shanghai:Shanghai Jiaotong University Press，1999:44-50.

［11］李彬彬，歐進萍.新型深吃水立柱平臺在極端海況下的動力性能分析［C］//第六屆全國土木工程研究生學術論壇，北京，2008:186-191.

［12］SUBRATA C.Handbook of offshore engineering［M］.Amsterdam:Elsevier，2005:427-437.

［13］DAVENPORT A G.Note on the distribution of the largest value of a random function with application to gust loading［J］.ICE Proceedings，196l，28(2):187-196.