關于一類含有線性算子的亞純多葉函數

徐能

（常熟理工學院數學與統計學院，江蘇常熟 215500）

關于一類含有線性算子的亞純多葉函數

徐能

（常熟理工學院數學與統計學院，江蘇常熟 215500）

引進和研究了一類含有線性算子的新的多葉亞純函數，得到了這一函數類中的一些有趣性質，如包含關系、卷積性質等.這些結果改進和拓展了早期的一些工作，同時也得到了其他一些新的結果.

亞純函數；多葉函數；凸單葉函數；Hadamard乘積（或卷積）；從屬；線性算子

1 預備與引理

設Σp表示由形如

組成的在去心單位圓盤U0={z:0＜|z|＜1}內解析的函數類.一個函數f(z)∈Σp被稱為是在類Σ*p(α)中，如果對某些α(α＜1)滿足條件

注意到對于0≤α＜1,Σ*p(α)是α階p葉亞純星型函數類.同時，我們寫Σ*1(α)=Σ*(α).

對于由（1.1）給出的f(z)∈Σp和g(z)∈Σp，這里

則f(z)和g(z)的Hadamard乘積（或卷積）定義為

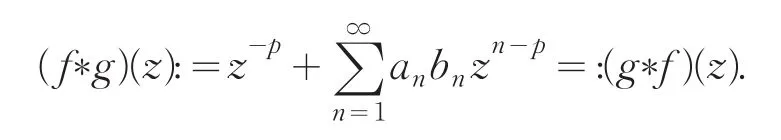
這里c?{0,-1,-2,…}，(x)0=1,(x)n=x(x+1)…(x+n-1)(n∈?).相應于函數φp(a,c;z)，廣義超幾何函數

現在我們定義函數φp(a,c;z)為

這里l≤m+1,l,m∈?0:=??{0},βj?{0,-1,-2,…}(j=1,2,…,m).現在我們定義

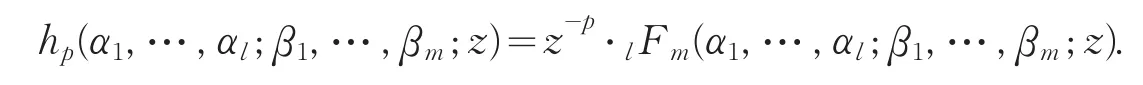
近來，Liu和Srivastava[1]通過下列Hadamard乘積

定義了一類新的線性算子

這里f(z)∈Σp,l≤m+1,l,m∈N0,βj?{0,-1,-2,…}(j=1,2,…,m).如果f(z)∈Σp由（1.1）給出，則從（1.3）和（1.4）我們有

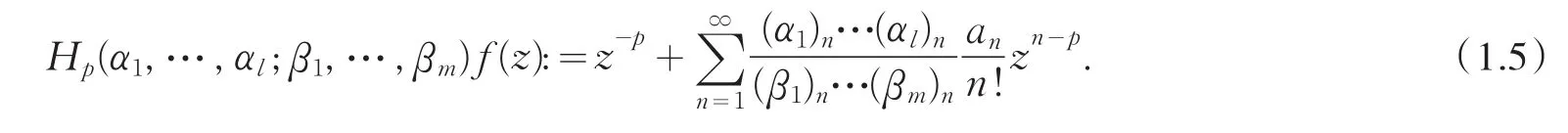
lFm(α1,…,αl;β1,…,βm;z)被定義為下列級數:

為了使記號簡便，我們引進

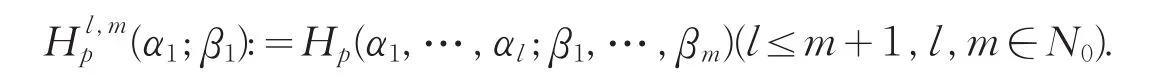
特別地，對于p=1,l=2,m=1和α1=a,α2=1,β1=c?{0,-1,-2,…},我們得到線性算子

這是由Liu和Srivastava[2]以及Yang[3]分別獨立引進和研究的.

令P是由在U內凸單葉并且滿足條件h(0)=1,Reh(z)＞0(z∈U)的解析函數所組成的函數類.

設f(z)和g(z)在U內解析.如果存在一個在U內的解析函數w(z)，使得

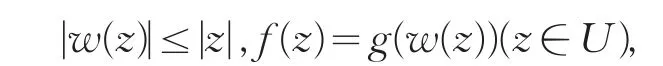
則稱函數f(z)是在U內從屬于g(z)，記為f(z)?g(z).進一步，如果g(z)在U內單葉，則

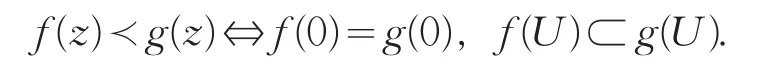
在整篇文章中，我們設

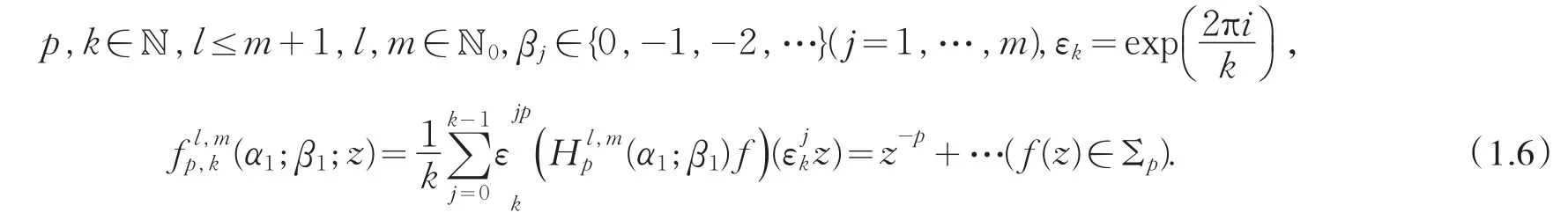
顯然，對于k=1,我們有

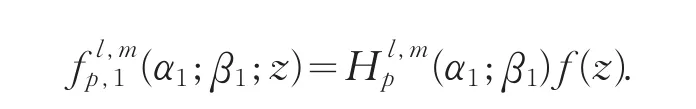
關于k-對稱點的亞純（或解析）函數類已經被許多學者所研究（見文獻[4-9]）.

在本文中，使用線性算子Hl,mp(α1;β1)和兩個解析函數間的從屬，我們引進和研究了下列Σp中的子類:

定義函數f(z)∈Σp如果滿足條件

導致函數類Σp,k(a,c;h)，這是最早由Srivastava，Yang和Xu（見文獻[5]）引進和研究的.有關亞純函數的研究

還可參見文獻[1-3，10-19]等.

為了導出我們的結果，需要下列引理.

在本文中，我們的目標是給出函數類Σl,mp,k(α1;β1;h)中的包含關系，卷積性質及其他一些新的結果.我們的結果改進和擴展了一些早期的結論.

2 卷積性質

定理1設h(z)∈P,α＜1且滿足

[1]Liu Jinlin，Srivastava H M.Classes of meromorphically multivalent functions associated with the generalized hypergeometric function [J].Math Comput Modelling，2004，39:21-34.

[2]Liu Jinlin，Srivastava H M.A linear operator and associated families of meromorphically multivalent functions[J].J Math Anal Appl，2000，259:566-581.

[3]Yang Dinggong.Certain convolution operators for meromorphic Functions[J].Southeast Asian Bull Math，2001，25:175-186.

[4]Sakaguchi K.On a certain univalent mapping[J].J Math Soc Japan，1959，11:72-75.

[5]Srivastava H M，Yang Dinggong，Xu Neng.Some subclasses of meromorphically multivalent functions associated with a linear operator[J].Appl Math Comput，2008，195:11-23.

[6]Sudharsan T V.On functions starlike with respect to symmetric and conjugate points[J].Taiwan J Math，1998（2）:57-68.

[7]Wang Z G，Gao C Y，Yuan S M.On certain subclasses of close-to-convex and quasi-convex functions with respect to k-symmetric points[J].J Math Anal Appl，2006，332:97-106.

[8]Yang Dinggong，Liu Jinlin.On Sakaguchi functions[J].Internat J Math Math Sci，2003，30:1923-1931.

[9]Yuan S M，Liu Z M.Some properties of α-convex and α-quasiconvex functions with respect ton-symmetric points[J].Appl Math Comput，2007，188:1142-1150.

[10]Aouf M K.Certain subclasses of meromorphically multivalent functions associated with generalized hypergeometric function[J]. Comput Math Appl，2008，55:494-509.

[11]Aouf M K.Argument estimates of certain meromorphically multivalent functions associated with generalized hypergeometric function[J].Appl Math Comput，2008，206:772-780.

[12]Cho N E，Kim I H.Inclusion properties of certain classes of meromorphic functions associated with the generalized hypergeometric function[J].Appl Math Comput，2007，187:115-121.

[13]Cho N E，Kwon O S，Srivastava H M.Inclusion and argument properties for certain subclasses of meromorphic functions associated with a family of multiplier transformations[J].J Math Anal Appl，2004，300:505-520.

[14]El-Ashwah R M.Some properties of certain subclasses of meromorphically multivalent functions[J].Appl Math Comput，2008，204:824-832.

[15]Liu Jinlin.Some properties of certain meromorphically multivalent Functions[J].Appl Math Comput，2009，210:136-140.

[16]Liu Jinlin，Srivastava H M.Subclasses of meromorphically multivalent functions associated with a certain linear operator[J].Math Comput Modelling，2004，39:35-44.

[17]Raina R K，Srivastava H M.A new class of meromorphically multivalent functions with applications to generalized hypergeometric functions[J].Math Comput Modelling，2006，43:350-356.

[18]Srivastava H M，Patel J.Applications of differential subordination to certain subclasses of meromorphically multivalent functions [J].J Inequal Pure Appl Math，2005，6（3）:1-13.

[19]Wang Z G，Jiang Y P，Srivastava H M.Some subclasses of meromorphically multivalent functions associated with the generalized hypergeometric function[J].Comput Math Appl，2009，57:571-586.

[20]Ruscheweyh S.Convolutions in Geometric Function Theory[M].Montreal:Les Presses de Universite de Montreal，1982.

[21]Ruscheweyh S.New criteria for univalent functions[J].Proc Amer Math Soc，1975，49:109-115.

[22]Xu Neng，Yang Dinggong.An application of differential subordinations and some criteria for starlikenedd[J].Indian J Pure Appl Math，2005，36:541-556.

[23]Suffridge T J.Some remarks on convex maps of the unit disk[J].Duke Math J，1970，37:775-777.

A Class of Meromorphically Multivalent Functions Involving a Linear Operator

XU Neng
(School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

meromorphic functions;multivalent functions;convex univalent functions;linear operator;convolu?tion;k-symmetric points;subordination

O174.5

A

1008-2794（2011）08-0001-09

2011-05-19

國家自然科學基金（10871094）資助項目.

徐能（1961—），男，江蘇常熟人，常熟理工學院數學與統計學院教授，研究方向：函數論.