一類與Virasoro代數有關的李代數的中心擴張

呂彥瑋，朱林生

（1.蘇州科技學院數理學院，江蘇蘇州 215011；2.常熟理工學院數學與統計學院，江蘇常熟 215500）

一類與Virasoro代數有關的李代數的中心擴張

呂彥瑋1，朱林生2

（1.蘇州科技學院數理學院，江蘇蘇州 215011；2.常熟理工學院數學與統計學院，江蘇常熟 215500）

通過計算生成元確定了一類Virasoro型李代數的二上同調群及其維數，進而給出了這類李代數的中心擴張李代數．

李代數；2-上循環；2-上邊緣；第二上同調群；普遍中心擴張

0 引言

Virasoro型李代數在數學和物理領域有廣泛的應用，已被廣泛研究，例如文獻[1]中的結果．本文我們考慮如下類型的李代數N有一組基{Lm,Mm,YP|m∈Z,p∈Z}并且滿足下列關系式：

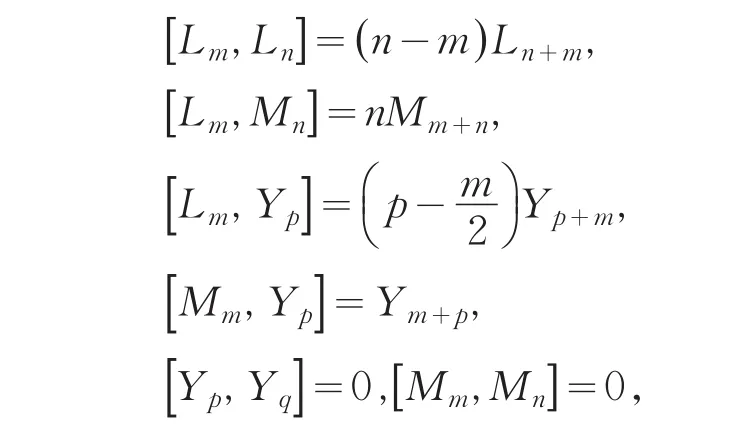
其中m，n，p，q∈Z.

在文獻[2]中，我們研究了該李代數的導子代數，證明了該李代數是完備李代數．本文我們研究李代數N的中心擴張．

1 主要結果

設g是一個李代數．雙線性函數ψ：g×g→C是g上的2-上循環，如果對所有的x,y,z∈g,下面兩個條件滿足：

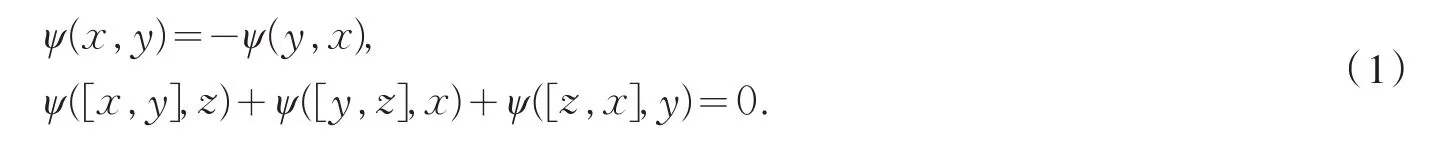
對任意線性函數f:g→C,我們可以定義一個2-上循環ψf：ψf(x,y)=f([x,y]),?x,y∈g.這樣的2-上循環稱為g上的2-上邊緣．

C2(g,C),B2(g,C)分別代表2-上循環和2-上邊緣的向量空間．則商空間H2(g,C)=C2(g,C)/B2(g,C)稱為g的第二上同調群．

下面是我們的主要定理.

定理1.1dim H2(N,C)=3.

證明設φ:N×N→C是N上的2-上循環，令f:N→C是一個線性映射定義如下：

即dim H2(N,C)=3.

下面討論中心擴張．首先回憶一些概念和已知結果．

設g是一個完滿李代數，即[g，g]=g.(g,π)稱為g的一個中心擴張，如果π:g→g是一個核在李代數g的中心的滿同態．若g也是完滿的李代數，則稱(g,π)是g的一個覆蓋．在文獻[3]中已經證明每一個完滿李代數都有一個普遍中心擴張．對于我們研究的完滿李代數N，令N=N⊕CCL⊕CCLM⊕CCM是一個復數域C上的向量空間，其基為{Ln,Mn,Yn,CL,CLM,CM|n∈Z}，滿足下面的關系式

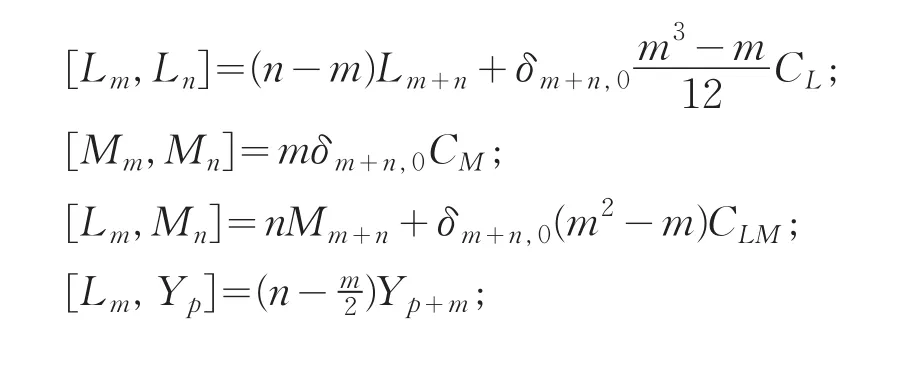
[4]，我們有下面的引理：

引理1.3李代數N的每個導子可提升為N的一個導子，并且這個提升是唯一的，且Der(N)?Der(N)．

證明因為N是N的普遍中心擴張，且由文獻[2]中推論2.10，C（N）=0，且N是一個完滿李代數．由推論1.2、引理1.3，我們有D(CL)=D(CLM)=D(CM),對所有的D∈Der(N)．因此結合文獻[2]中定理2.4，我們有Der(N)=Inn(N)．

參考文獻：

[1]Gao S,Jiang C,Pei Y.Structure of the extended Schr?dinger-Virasoro Lie algebra[J].Alg Colluq,2009,16:549-566.

[2]呂彥瑋，朱林生.一類李代數的導子代數[J].常熟理工學院學報，2011，25（2）：6-10．

[3]Garland H.The arithmetic theory of loop groups[J].Publ Math IHES,1980,52:5-136.

[4]Benkart G M,Moody R V.Derivations,central extensions and affine Lie algebras[J].Algebras Groups Geom,1986（4）:456-492.

Central Extensions of a Class of Lie Algebra Related to Virasoro Algebra

LV Yan-wei1,ZHU Lin-sheng2
(1.School of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,China；2.School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

Through the calculation of generators,we determine second cohomology group and dimension of a class of Lie algebra related to Virasoro algebra.Then its central extensions are given out in this paper.

Lie algebra;2-cocycle;2-coboundary;second cohomology group;universal central extensions

O152.5

A

1008-2794（2011）08-0010-05

2011-05-19

蘇州科技學院2010年度研究生科研創新計劃項目（SKCX10S_027）．

呂彥瑋（1985—），女，河北石家莊人，蘇州科技學院數理學院基礎數學專業2008級研究生．

朱林生（1962—），男，江蘇吳江人，常熟理工學院數學與統計學院教授，博士，研究方向：李代數，E-mail: lszhu@cslg.edu.cn．