一類新超混沌系統(tǒng)及其自同步

高智中

（安徽科技學院理學院，安徽鳳陽 233100）

一類新超混沌系統(tǒng)及其自同步

高智中

（安徽科技學院理學院，安徽鳳陽 233100）

基于一個三維混沌系統(tǒng)構(gòu)造了一個新的四維超混沌系統(tǒng)，利用系統(tǒng)的分岔圖、Lyapunov指數(shù)譜圖和相圖分析方法研究了該系統(tǒng)的運動規(guī)律.根據(jù)線性系統(tǒng)穩(wěn)定性定理，設計了一種非線性反饋控制器，實現(xiàn)了該超混沌系統(tǒng)的自同步，數(shù)值模擬結(jié)果驗證了理論分析的正確性.

新超混沌系統(tǒng)；分岔圖；Lyapunov指數(shù)譜；相圖；穩(wěn)定性定理；自同步

由于超混沌系統(tǒng)有兩個或兩個以上正的Lyapunov指數(shù)，系統(tǒng)的動力學行為比一般混沌系統(tǒng)具有更強的隨機性和更高的不可預測性，在混沌保密通信及信息安全等領(lǐng)域中具有更高的實用價值.因此，構(gòu)建高維超混沌系統(tǒng)并實現(xiàn)高維系統(tǒng)的同步是當前非線性科學領(lǐng)域研究的熱點課題，近年來取得了豐碩的成果[1-5].

本文在文獻[6]提出的新三維自治混沌系統(tǒng)的基礎(chǔ)上構(gòu)造了一個新的超混沌系統(tǒng)，利用系統(tǒng)的分岔圖、Lyapunov指數(shù)譜圖和相圖分析方法研究了該系統(tǒng)的運動規(guī)律.然后利用非線性反饋控制法實現(xiàn)了該超混沌系統(tǒng)的自同步.由于其控制結(jié)構(gòu)簡單，易于操作，不僅可以應用于混沌控制，而且還可以應用于混沌同步.數(shù)值模擬結(jié)果驗證了理論分析的正確性.

1 新超混沌系統(tǒng)的設計

文獻[6]提出的新三維自治混沌系統(tǒng)，其狀態(tài)方程可表示為：

當a=5,b=90時，系統(tǒng)處于混沌狀態(tài).

根據(jù)超混沌產(chǎn)生的必要條件[7]，在這個三維系統(tǒng)上增加一個非線性狀態(tài)反饋控制器x4，并增加一個一階微分方程，可得到如下的四維超混沌系統(tǒng)：

式中，m為新引入的參數(shù).Lyapunov指數(shù)是在混沌系統(tǒng)中定量地描述狀態(tài)空間吸引子的相鄰軌線收縮和擴張的量，是吸引子類型的有效判據(jù).當選取參數(shù)a=5,b=90,m=3.4時，利用Wolf方法[8]數(shù)值計算系統(tǒng)的四個Lyapunov為λ1=0.7204,λ2=0.0579,λ3=-0.017,λ4=-5.7608，其中有兩個正的Lyapunov指數(shù)，并且所有Lyapunov指數(shù)之和小于零，說明系統(tǒng)在這組參數(shù)下處于超混沌狀態(tài)，此時系統(tǒng)的Lyapunov維數(shù)為3.1347，由于該系統(tǒng)的Lyapunov維數(shù)是分數(shù)維數(shù)，從而從另一方面驗證了系統(tǒng)在這組參數(shù)下處于超混沌狀態(tài).因此所設計的四維系統(tǒng)的確是一個超混沌系統(tǒng).

2 超混沌系統(tǒng)的簡單動力學分析

非線性混沌動力系統(tǒng)的主要動力學特性可通過分岔分析和計算Lyapunov指數(shù)譜來分析.

當固定參數(shù)a=5，b=90，系統(tǒng)變量x隨m在[0,10]變化時的分岔圖和Lyapunov指數(shù)譜圖（為了將系統(tǒng)的第二根Lyapunov指數(shù)大于零的部分更加明顯，這里略去了第四根Lyapunov指數(shù)曲線）如圖1（a）和（b）所示.從圖1可以觀察到，系統(tǒng)一開始處于混沌態(tài)，隨著m的增大，系統(tǒng)進入超混沌態(tài)，然后進入較窄的周期態(tài)，接著又進入擬周期態(tài)，最后進入穩(wěn)定的周期一狀態(tài).圖2（a-f）給出了x1-x3平面的六種典型的吸引子.

3 超混沌系統(tǒng)的自同步

將所構(gòu)造的四維超混沌系統(tǒng)（1）作為驅(qū)動系統(tǒng)，再取如下的系統(tǒng)（2）為響應系統(tǒng).

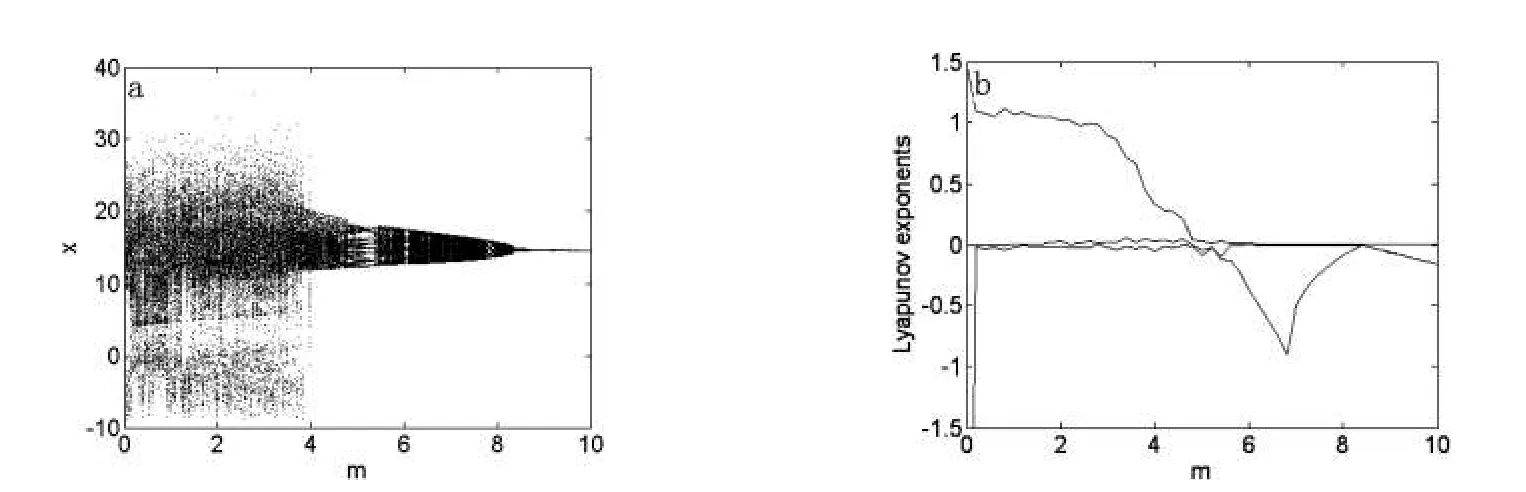
圖1 系統(tǒng)的分岔圖（a）和Lyapunov指數(shù)譜圖（b）

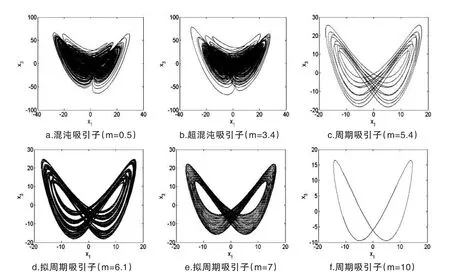
圖2 超混沌系統(tǒng)的典型平面吸引子

為了獲得能夠?qū)崿F(xiàn)驅(qū)動系統(tǒng)與響應系統(tǒng)同步的非線性反饋控制器，令兩系統(tǒng)的誤差變量，則可得到誤差系統(tǒng)為

設計了如下一個簡單的非線性控制器

線性系統(tǒng)穩(wěn)定性定理[9]：對于線性系統(tǒng)，其唯一平衡點漸近穩(wěn)定的充要條件是A的所有特征值均具有負實部.

顯然誤差系統(tǒng)的4個特征值為-5,-1,-1,-1，根據(jù)線性系統(tǒng)穩(wěn)定性定理知誤差系統(tǒng)可在式（4）的控制下，其零解是漸近穩(wěn)定的，從而可使驅(qū)動系統(tǒng)（1）和響應系統(tǒng)（2）同步.下面利用四階龍格-庫塔法對誤差系統(tǒng)進行數(shù)值模擬，選取相同的參數(shù)a=5，選取驅(qū)動系統(tǒng)初值為(1,1,1,1)，響應系統(tǒng)初值為(10,10,10,10)，時間t的步長為0.001.在非線性控制器（4）式作用下系統(tǒng)（1）和（2）的同步誤差曲線模擬結(jié)果如圖3所示，由圖3可以看出，數(shù)秒后誤差變量e1,e2,e3,e4全部趨向于零，這表明驅(qū)動系統(tǒng)與響應系統(tǒng)已達到了同步.數(shù)值模擬結(jié)果證明了所設計的非線性控制器的正確性和有效性.

圖3 誤差系統(tǒng)的時序圖

4 結(jié)論

本文構(gòu)造了一個新的四維超混沌系統(tǒng)，利用系統(tǒng)的分岔圖、Lyapunov指數(shù)譜圖和相圖分析方法研究了新引入?yún)?shù)m取不同值時超混沌系統(tǒng)的運動情況.根據(jù)線性系統(tǒng)穩(wěn)定性定理，設計了一種簡單的非線性反饋控制器實現(xiàn)了該超混沌系統(tǒng)的自同步，且其同步是全局漸近穩(wěn)定的.所得結(jié)果為該超混沌系統(tǒng)在混沌保密通信中的應用提供了理論參考.

[1]高智中.超混沌Liu系統(tǒng)的自同步研究[J].湖南文理學院學報，2011，23（2）：28-30．

[2]劉揚正，林長圣，姜長生.新的四維超混沌Liu系統(tǒng)及其混沌同步[J].電子科技大學學報，2008，37（2）：235-237，296．

[3]李瑞紅，陳為勝，李爽.超混沌Lorenz系統(tǒng)的投影同步及其在保密通信中的應用[J].電路與系統(tǒng)學報，2011，16（2）：41-45．

[4]方潔，姜長生.錯位修正混沌函數(shù)投影同步及在保密通信中的應用[J].四川大學學報，2011，43（2）：136-141．

[5]孫寧，張化光，王智良.基于分數(shù)階滑模面控制的分數(shù)階超混沌系統(tǒng)的投影同步[J].物理學報，2011，60（5）：1-7．

[6]Buncha M，Banlue S.A new five-term simple chaotic attrators[J].Physics Letters A，2009，373（1）：4038-4043．

[7]Rossler O E.An equation for hyperchaos[J].Physics Letters A，1979，71（2-3）:155-157．

[8]Wolf A，Swift J B，Swinney H L，et al.Determining Lyapunov exponents from a time series[J].Physica D：Nonlinear Phenomena，1985，16（3）：285-317．

[9]鄭大中.線性系統(tǒng)理論[M].北京：清華大學出版社，1992．

A Novel Hyperchaotic System and Its Anti-synchronization

GAO Zhi-zhong
（College of Science,Anhui Science and Technology University，F(xiàn)engyang 233100,China）

A new four-dimensional hyperchaotic system based on a three-dimensional chaotic system is built in the paper.The hyperchaotic system is analyzed by bifurcation diagram Lyapunov exponents spectrum diagram and phase diagram.According to the linear system stability theorem,we design a nonlinear feedback controller to achieve anti-synchronization of the hyperchaotic systems.Numerical simulation results verify that the theoreti?cal analysis is correct.

new hyperchaotic system;bifurcation diagram;Lyapunov exponents spectrum

O545

A

1008-2794（2011）08-0031-04

2011-06-23

安徽科技學院校自然科學項目（ZRC2010260）.

高智中（1979—），男，山西神池人，安徽科技學院理學院助教，碩士，研究方向：混沌反控制.