平穩小波濾波算法在泳池報警系統中的應用

雷 飛，宮君樂，趙曉霞

LEI Fei,GONG Jun-le,ZHAO Xiao-xia

（北京工業大學 電子信息與控制工程學院，北京 100022）

0 引言

對于泳池報警系統來講，主要分為視頻采集部分與事件推理兩部分[1]。在視頻采集部分中，由于光照，游泳所產生池水晃動和氣泡，以及水中各種倒影的影響，水下攝像頭得到的圖像會受到各種干擾，圖片質量特別差，因此圖像去干擾便成了處理中最為關鍵的環節之一。小波算法具有時頻局部化和多尺度分析能力[2]，有效改進了傅里葉變換和Gobor變換存在的不足，被稱之為分析信號的顯微鏡，所以基于小波的圖像處理方法在圖像各個領域具有很好的發展前景。

通過傳統離散正交小波變換軟閾值處理時[3,4]，得到的圖像往往邊緣比較模糊，而采用硬閾值算法進行處理，當閾值選取過小時，干擾濾除效果不明顯，若采用較大的閾值時，一些邊緣信息往往會被濾除。因此文中采用平穩小波變換進行圖像濾波平滑處理，實驗結果顯示經處理后的圖像不僅干擾去除明顯，而且邊緣保存良好。

文中第一部分給出傳統小波變換以及平穩小波變換的算法原理，第二部分詳細論述了閾值的選取和算法實現步驟。第三部分給出實驗結果，并進行對比。最后對文章進行了總結。

1 算法原理

首先，我們假設所采集到的圖片為f(x,y)，其中x、y分別為圖像橫軸與縱軸坐標，f(x,y)為得到的離散的值為灰度值[5]。

1.1 傳統小波變換算法原理

假設ALL,0(x,y)=f(x,y)，其中ALL,0(x,y)為未進行小波變換之前的圖像系數，然后對其分解運算[6,7]：

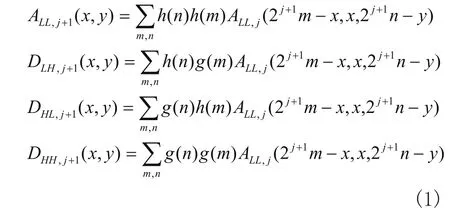
其中h(.)g(.)分別為低通和高通濾波器，ALL,0(x,y)=f(x,y)為近似圖像，DLH,j+1(x,y)DHH,j+1(x,y)L分別為小波變換后水平垂直和對角分量。

小波分解示意圖如圖1所示。

圖1 小波分解示意圖

對圖像進行消噪后必須對其進行小波系數重構，從而得到重構后的圖像，小波重構算法如下：

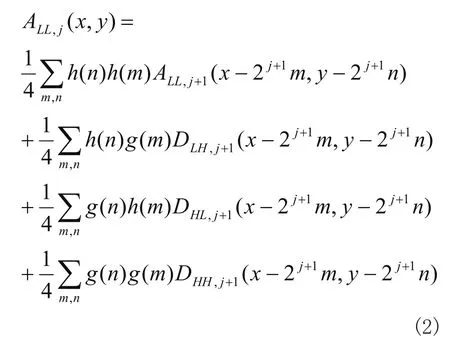
其中 為重構后的圖像。

小波重構示意圖如下所示：

圖2 小波重構示意圖

1.2 平穩小波變換算法原理

平穩小波變換是對傳統小波變換的改進算法，它是一種非正交的小波變換，具有冗余性和平移不變性[8]。它們之間最大區別是：濾波后不會對所產生的數據進行采樣。因此，對圖像進行平穩小波變換后所得到的低頻系數和高頻系數與原圖像像素數相等，另外，為了保持變換后能量的統一性，對于濾波器的系數進行了修改，即對濾波器進行補零插值處理。

假設傳統小波濾波器低通和高通濾波系數分別為h0(k)、g0(k)，則尺度j上的平穩小波濾波器hj、gj的系數分別改為

關系圖如圖3所示。

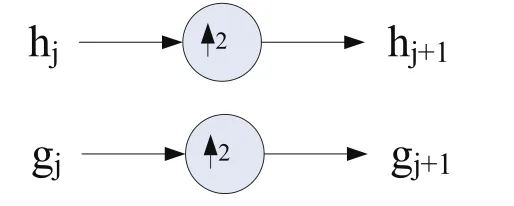
圖3 濾波器插值示意圖

2 算法實現

2.1 閾值選取

圖像經小波變換后通常要進行閾值處理以去除干擾，為保證圖像的基本信息不變，必須首先保留小波變換后所有低頻小波系數，然后采用閾值法對高頻系數進行處理。閾值的選取主要分為兩種：硬閾值和軟閾值。

閾值選取：

式中Tj表示小波分解第j層的閾值。

σj表示第j層高頻系數的標準方差，一般工程應用情況下σj=Median(|X|)/0.6745。

N表示所對應尺度方向上的小波系數個數。

硬閾值處理：

假設Wj,k表示第j層小波系數值。

硬閾值處理：

將原始圖像的小波系數與所計算的閾值進行比較，當Wj,k大于等于閾值Tj時保留原值，否則將其置零。

軟閾值處理：

將原始圖像的小波系數與所計算的閾值進行比較，將Wj,k大于閾值的像素點收縮為該點值與閾值的差，小于閾值相反數的像素點收縮為該點值與閾值的和，幅值小于閾值的像素點置零。

硬閾值法和軟閾值法雖然在實際工程中得到了廣泛的應用，但是兩種方法本身都存在一些缺陷，如硬閾值法在閾值處不連續，因此重構可能產生一些震蕩；雖然軟閾值法連續，但是由于收縮處理使得估計出的小波系數和分解前的小波系數存在一定的偏差，這就直接影響了重構信號與真實信號的準確性。因此采用一種改進的半軟閾值函數對變換后的小波系數進行處理：

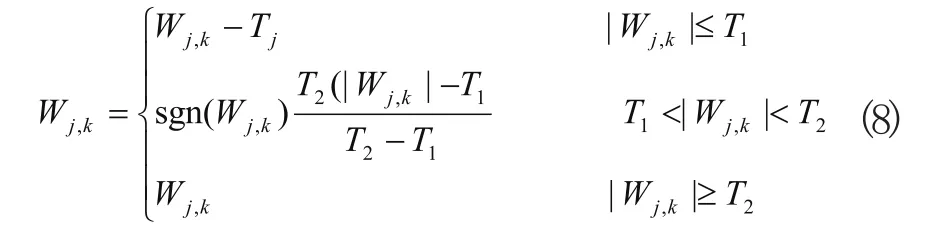
式中sgn()為符號函數，由上式可以看出，當T1=T2時，上式就轉化為硬閾值法，當T2趨于無窮大時上式就變為軟閾值法。通過合理的選取T1和T2的值，可以在硬閾值和軟閾值的方法之中達到很好的效果。

2.2 算法步驟

平穩小波濾波算法具體流程如下：

1）獲取原圖像。

2）對所得圖像用二維平穩小波變換進行多尺度分解。

3）計算各高頻系數標準方差σj，并確定閾值 。

4）采用改進的閾值法對平穩小波變換后的高頻系數進行閾值處理。

5）對閾值處理后的系數進行平穩小波反變換，從而得到平滑后的圖像。

3 實驗結果分析

實驗工具采用 MATLAB 7.8.0進行仿真，圖片大小為（288×352）。實驗中我們選取db2小波對其進行仿真，傳統小波變換分解3層，平穩小波變換分解5層，采用改進閾值函數進行處理，圖4為對采集圖片進行三種方法濾波仿真后對比結果。圖5為采用canny算子提取濾波后的圖像邊緣的對比結果。

圖4 濾波平滑后結果對比圖

從仿真結果圖4可以看出軟閾值正交小波濾波后人體邊緣變的模糊，出現偽Gibbs和振鈴現象，經實驗，若是分解層數過多，這種現象會變的非常嚴重。采用硬閾值正交小波濾波后，圖像質量相對于原圖像視覺效果上有了一些提高，但效果相對不是特別明顯。采用平穩小波濾波算法經改進的閾值函數進行處理，由結果可以看出，不但平滑效果良好，而且目標邊緣部分得到很好保持。最后用canny算子進行邊緣檢測，由圖5結果可以看出，采用平穩小波變換后圖像干擾去除明顯，并且目標的邊緣保持依然良好。

圖5 canny邊緣檢測結果對比圖

4 結論

本文利用平穩小波濾波算法對圖像進行多層分解，由于平穩小波變換濾波后不進行下采樣處理，變換后得到的水平、垂直、對角分量與原圖像的像素個數相等，從而有效保留了圖像必要的邊緣信息，并且經改進的閾值處理后大量去除了不必要干擾因素，滿足了泳池報警系統的要求。經大量實驗結果表明，本方法相對于傳統小波變換，不僅平滑效果良好，而且有效保留了目標的邊緣信息，為整個泳池系統目標提取、溺水判斷等后續工作的開展奠定了基礎。

[1] How-Lung Eng,Kar-Ann Toh and Junxian Wang"A live visual surveillance system for early drowning detection at pool,"IEEE transactions on circutts and system for widbo technology,2008,18.

[2] Chaoying Liu,Huibin Wang and Yixin Wang."Image denoising based on wavelet edge detection by scale multiplication,"Proceeding of the 2007 IEEE international congerence on integration technology March 20-24,2007,Shenzhen,China.

[3] Qinwu Zhou,Lizhuang Liu,Zhengzhong Bian."Denoise and contrast enhancement of ultrasound speckle image based on wavelet," ICSP02 Proceeding.

[4] Xingmei Li,Guoping Yan,and Liang Chen."Image denoise based on soft threshold and edge enhancement,"Second workshop on digital media and its application in museum and heritage.May 3,2007,Wuhan,China.

[5] Rafael C.Gonzalez,and Richard E. Woods."Digital image processing". December,2007.

[6] Quan Pan,Lei Zhang,Guanzhong Dai,and Hongcai Zhang."Two denoising methods by wavelet transform,"IEEE transactions on signal processing,1999,47,12.

[7] Zhenxian Lin,Guoxiang Song,and Xue Wen."Two improved method on wavelet image denoising.," Proceedings of the second international conference on machine leaning and cybernetics,Xi'an,2-5 November 2003.

[8] 劉成云,陳振學,常發亮.基于平穩小波的自適應閾值MR圖像去噪法[J].山東大學學報,2009,10：222-226.