消防出警路線選擇算法的研究

2011-04-23 12:11:04瞿詩高長江大學工程技術學院湖北荊州434020

長江大學學報(自科版) 2011年7期

瞿詩高 (長江大學工程技術學院,湖北荊州434020)

我國每年有大量的火災發生,對人民生命財產安全造成了嚴重的威脅。如果能夠提高消防戰士的出警速度,減少消防官兵到達火災現場所需要的時間,將會極大地減少火災帶來的損害。我國現有的消防系統在出警道路的選擇上采用人工方式,即由調度人員根據火警現場、道路等情況為出警戰士選擇和指示出警道路。當可選道路較多、人流等復雜情況下,調度人員就無法確保選出最優出警路線。為此,筆者基于遺傳算法研究了一種消防出警道路選擇算法,利用該算法可選擇最佳消防出警路線,從而保證消防戰士利用最短出警時間到達火警現場。

1 數學模型

1.1 主要定義

使用有向圖G(V,E)表示當前的道路交通圖(見圖1)。其中,V={v0,v1,…,vn},是道路的拐點的集合,v0是消防隊的位置;E為道路的集合,其元素eij用于描述從道路節點vi到vj的道路,該元素使用三元組(lij,wij,dij)進行描述,其中lij表示道路的長度,wij表示道路的寬度,dij表示道路當前的人流密度。

Psd表示從節點vs到節點vd之間的通路表達式:

圖1 有向圖G(V,E)

1.2 相關計算

消防車通過道路eij的時間為tij,即:

式中,v表示當前消防車的行駛速度,m/s。

消防車通過通路Psd的時間Ts d為消防車通過道路eij的時間之和:

通路Ps d的長度L(Psd)表示該通路上所有道路的長度之和:

1.3 優化目標的設定

由于消防出警的目標是以最快的速度到達火警現場,因此,將消防出警道路選擇問題描述為:已知道路交通情況,包括每條道路的寬度、長度、人流密度等的情況下,將車輛出警時間最小化,同時將出警通路長度最小化,即在有向圖上尋找2個目標節點之間的一條可行路徑 (見圖2)。

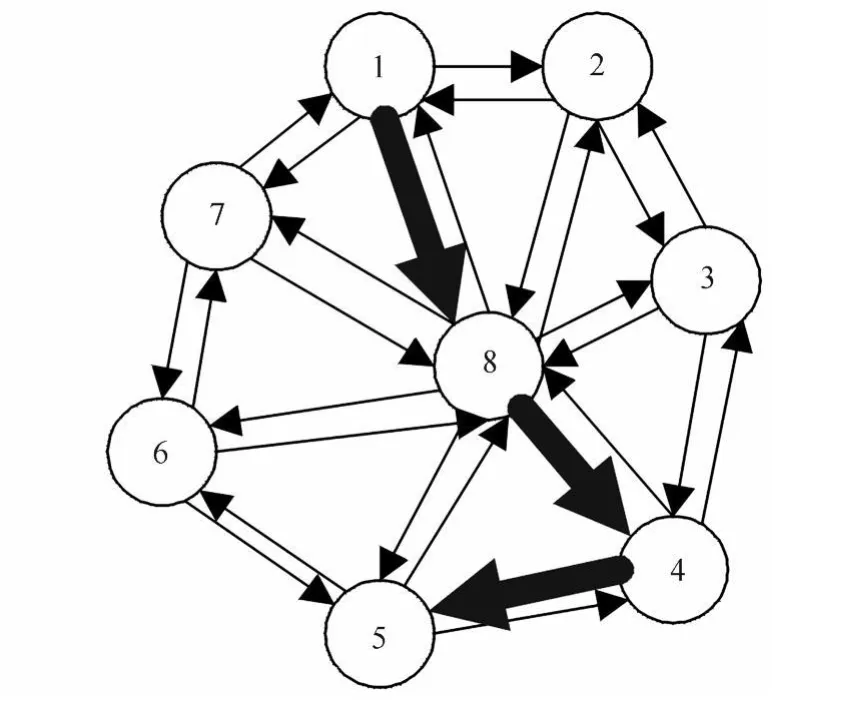
圖2 節點1-節點5之間的一條可行路徑

2 消防出警路線選擇算法

路徑選擇算法是NP難問題[1],當消防出警路線較多時,可選擇遺傳算法[2]求解。下面對該算法進行具體描述。

2.1 解的編碼

采用數值編碼方式,遺傳算法中的每個染色體對應一個解,染色體的長度等于n(n代表道路交通路中的節點數量);基因值為0,表示對應的道路拐點在通路上,否則不在。由此,染色體是以1開頭的一組基因。種群中的染色體是隨機生成的,種群規模為P。染色體中的基因組可能無法構成一條通路,否則為不合法染色體,應由新生成的染色體替換。

2.2 適應度函數設計

將Tsd和L(Psd)的加權和作為算法的適應度函數:

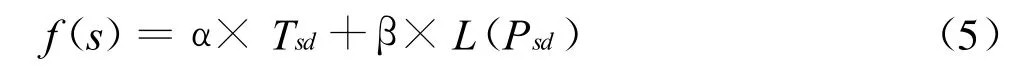
式中,s是問題的解;α和β代表權重系數,α+β=1,由于減少時間是最重要的優化目標,因而α需要占更大比例。

2.3 遺傳算子及算法中止條件

1)遺傳算子遺傳算子分為如下3種:①交叉算子。在交叉操作中采用單點平行交叉策略,隨機選擇某個基因位執行交叉。②變異算子。在變異操作中也采用單點變異策略,根據交叉概率用隨機生成的新數值替換隨機選取的基因位al的值。為保證新的染色體合法,新基因位的取值范圍要滿足解的編碼規范。在進化過程中,每代的最優染色體不參與變異操作。③選擇算子。選擇操作中應用精英保留策略,即最優染色體直接進入下一代種群中,其余染色體通過賭輪法進行選擇[3]。

2)終止條件使用最大不進化代數作為算法終止條件,若安全閥中的精英染色體經過最大進化次數后仍沒有更新,即種群沒有進化,則算法結束。

2.4 算法流程

使用遺傳算法的基本步驟如下:①根據結點編碼和種群規模P,隨機生成P個染色體,作為初種群。②根據式 (5)計算每個染色體的適應度函數值即適應值。③根據交叉和變異算子對種群執行交叉和變異操作,則種群中規模會增加。④根據選擇算子執行選擇操作,使新種群的規模恢復到P。⑤根據終止條件,判斷是否滿足終止條件,如果不滿足終止條件,則轉步驟②。⑥算法結束。