一種基于EMD的系統誤差分離方法

李世平，付 宇，張 進

（第二炮兵工程學院，陜西 西安 710025）

0 引 言

對儀器的測量誤差進行修正，提高測量準確度，其關鍵技術是如何分離測量數據中的系統誤差與隨機誤差。測量誤差分離程度的好壞直接關系到修正的效果。

測量誤差的分離方法現在使用較多的主要有最小二乘回歸法、中值濾波法、傅里葉級數逼近法、小波和小波包分解法等。最小二乘回歸法在誤差分離中存在模型階數確定困難；中值濾波法誤差分離準確度難以提高；Fourier級數逼近、小波和小波包分解法，都屬于基于基函數的分離方法，Fourier級數逼近法采用三角基函數逼近，選用不同的基函數，會得到不同的分離結果，但基函數的選擇本身就是難點。針對上述問題，提出了基于經驗模態分解（EMD）誤差分離的一種新方法，EMD分解的基函數是不確定的，它在分解過程中依賴于誤差信號本身，是自適應的。對于不同的誤差信號，基函數的選擇是不同的，也可以說這種分離方法采用的是一種自適應廣義基。盡管無法給出基函數的確切表達式，但由于依賴于誤差信號本身是自適應的，所以能夠通過這樣的廣義基得到非常好的分離效果。由于EMD分解是自適應性分解，這種自適應性表現為在不同的局部時間內其時間尺度是可以不同的，上一級基本模式分量的所有時間尺度不一定需要全部小于下一級的時間尺度，各個基本模式分量內時間尺度的變化完全是由誤差信號本身的特性決定的[1]。

1 誤差特征分析

根據誤差理論可知，誤差按照其性質和特點可以分為系統誤差、隨機誤差和粗大誤差3種。

1.1 系統誤差

系統誤差是指在重復性條件下，同一被測量無窮多次測量結果的均值與該被測量真值之差，其主要特征是具有規律性[2]。由于儀器自身的測量原理、組成結構、存放與使用環境因素的影響和操作的直接作用，使得系統誤差具有一定的變化規律。存在有不變的系統誤差、線性變化的系統誤差、指數變化的系統誤差、周期函數變化的系統誤差和復雜規律變化的系統誤差5種形式。

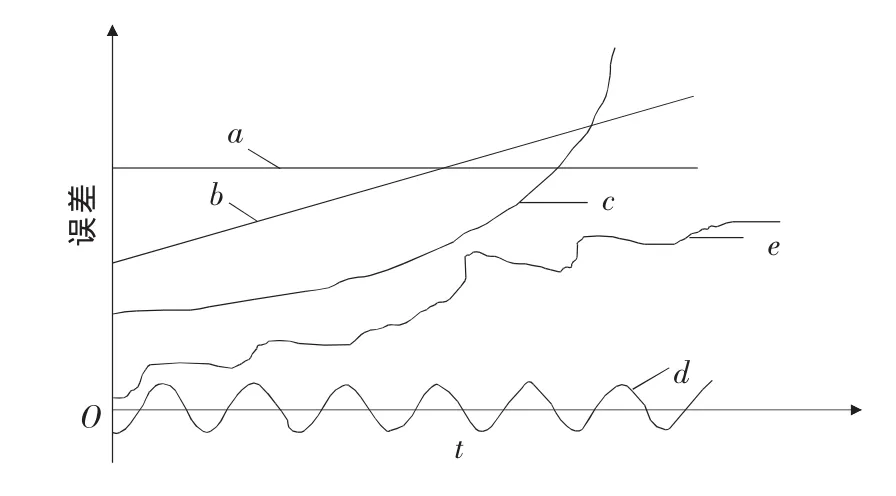
圖1 系統誤差的特征

圖1所示為各種系統誤差隨時間變化而表現出不同的特征。曲線a為不變的系統誤差；b為線性變化的系統誤差；c為指數函數系統誤差；d為周期函數系統誤差；e為復雜規律便變化的系統誤差[2]。

1.2 隨機誤差

隨機誤差是指相同測量條件下，誤差的大小和符號的變化均沒有固定規律。因此，隨機誤差的特征是沒有規律性、不可預見性和不可控制性。然而就其的總體而言，隨機誤差具備有界性、對稱性和抵償性，具有統計規律性。隨機誤差用概率統計的方法進行處理。

1.3 粗大誤差

超出在規定條件下預期的誤差，此誤差較大，明顯歪曲測量結果，通常不包含在合理的測量數據中。

2 經驗模態分離原理

2.1 EMD方法原理[3]

美國宇航局的Huang等于1998年提出了固有模態函數（IMF）的概念以及將任意信號分解為固有模態函數的方法，即經驗模態分解（EMD）。由EMD分解產生的IMF是根據信號本身的特點自適應得到的，分解出來的固有模態函數滿足以下2個條件：

（1）在整個數據序列中，極值點和過零點的數目相等或最多相差1個。

（2）在任意時間點上，信號極大值確定的上包絡線和極小值確定的下包絡線的均值為零。

EMD分解就是將信號分解成一系列表征信號特征時間尺度的IMF，其結果是將信號中不同尺度的波動或趨勢逐級分解，產生一系列具有不同特征尺度的數據序列，每一序列就是IMF。

信號數據x（t）進行EMD分解的步驟如下：

（1）首先找出x（t）上所有極值點，將所有極大值點和所有極小值點分別用三次樣條插值函數擬合出x（t）上、下包絡線，上、下包絡線間應包含所有的信號數據。將2條包絡線的平均值記為m1，x（t）與m1的差記作h1，即

在理想情況下，h1應為一個IMF分量。但事實上，由于包絡擬合中過沖和欠沖現象的存在，會產生新的極值點。因此，分解必須進行多次。

在第2次分解中，把h1看作待處理數據，其包絡均值為m11，則有

該過程重復k次，得到

直到h1k滿足IMF的條件為止，于是得到第1個IMF分量，記作

它表示信號數據序列中最高頻率的分量。

為了保證IMF分量有意義，必須確定一個停止準則。為此，Huang等人提出限制標準差SD的值來停止分解。SD的表達式如下：

當SD小于預先設定的值時，分解就停止。SD的值常取0.2～0.3之間。

（2）用x（t）減去c1（t），得到去掉高頻成分的新數據序列r1（t）為

將r1（t）視為新的x（t），重復以上過程，依次得到第2個IMFc2（t），…，cn（t）或rn（t）滿足終止條件分解終止。由此可得x（t）的分解式為

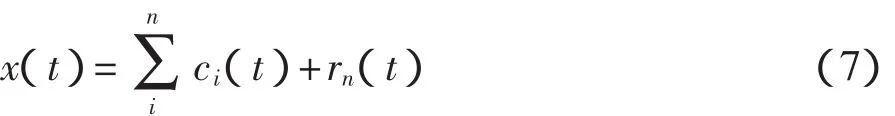
式中：rn（t）——殘余函數，代表信號的趨勢項；

c1（t），c1（t），…，cn（t）——信號從高到低不同頻率的分量。

通常，EMD分解出來的前幾個IMF分量集中了原信號中最顯著、最重要的信息[3]。

2.2 系統誤差的分離

按照系統誤差的特點，雖然存在有各種不同形式，但其變化是有規律的。根據該文前面介紹的內容可知，通過EMD分解得到的IMF分量和趨勢項來確定、提取系統誤差。

從IMF分量和趨勢項函數中判定系統誤差，應該按照系統誤差的形式進行確定，根據系統誤差的諸多形式，趨勢項函數一定屬于某種形式的系統誤差[2，4]。如何提取按周期規律變化的系統誤差，應當按照系統誤差的性質和其確定的規律性特點來判定，當存在不同頻率IMF分量函數時，低頻IMF分量函數應屬于周期性系統誤差，高頻IMF分量函數是否屬于周期性系統誤差是不能直接確定的。該文采用自相關分析的方法對高頻IMF分量函數進行提取周期性系統誤差。

自相關分析的目的是確定信號在不同時間的依賴關系或相似程度[1]，是提取信號周期的常用方法，可提取混有噪聲的周期信號，但前提條件是信噪比較高[5]。對于高頻IMF分量函數的系統誤差分離方法，實際上是小周期性系統誤差的分離。首先采用經驗模態分解法將誤差分解到各個IMF分量函數，達到降低噪聲誤差的作用；然后采用自相關分析法，判別每個IMF分量中是否含有淹沒于噪聲誤差中的周期信號，進而利用頻譜圖，提取該系統誤差的頻率；最后對含有的小周期性系統誤差進行擬合。

2.3 隨機誤差的分離

對于合理測量誤差數據，它是由系統誤差和隨機誤差兩部分組成的，在一定條件下，當已知其中某一誤差分量，另一部分誤差分量可求出。在使用EMD誤差分離方法分離出測量誤差的系統誤差分量后，如若系統與隨機誤差是代數和組合形式，隨機誤差分量通過測量誤差數據減去系統誤差即可得到。否則，使用單獨的分離隨機誤差的方法分離。

3 系統誤差的分離與仿真

按照系統誤差的變化特征，分別對系統誤差為線性變化、指數變化、冪函數變化和周期變化的4種情況進行仿真實驗，說明EMD分解提取系統誤差的有效性。

設仿真誤差x（t）由兩部分組成，一部分是干擾誤差函數 s（t），另一部分是系統誤差函數 d（t），即

為了仿真方便，這里假設干擾誤差函數s（t）的表達式為

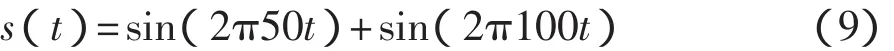
當然干擾函數也可以取任何其他函數或白噪聲函數。

3.1 系統誤差為線性變化

系統誤差 d（t）的表達式為

對誤差x（t）進行EMD分解，其結果如圖2所示。

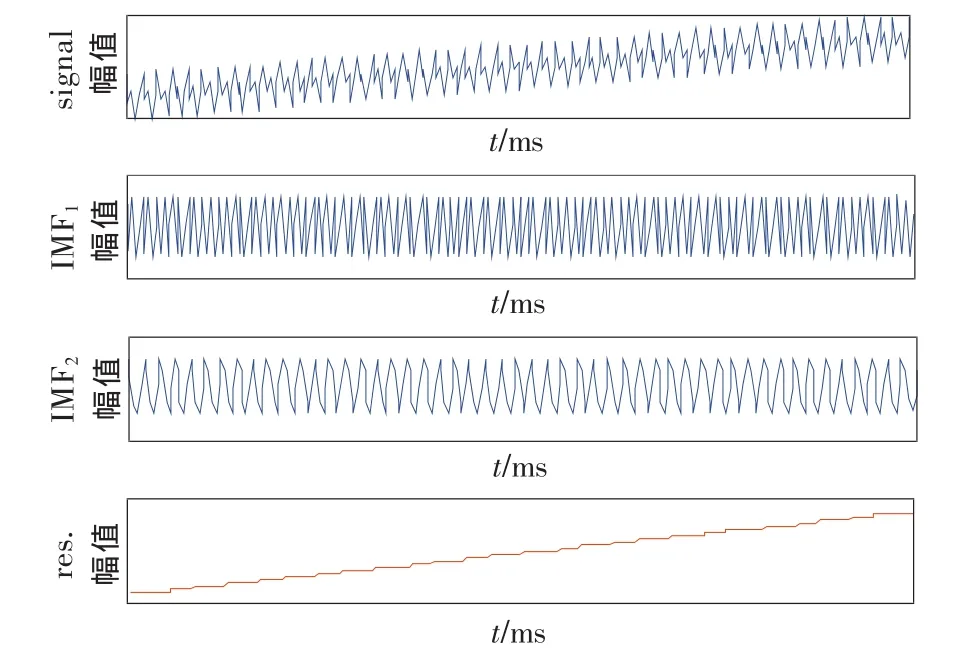
圖2 EMD分解結果

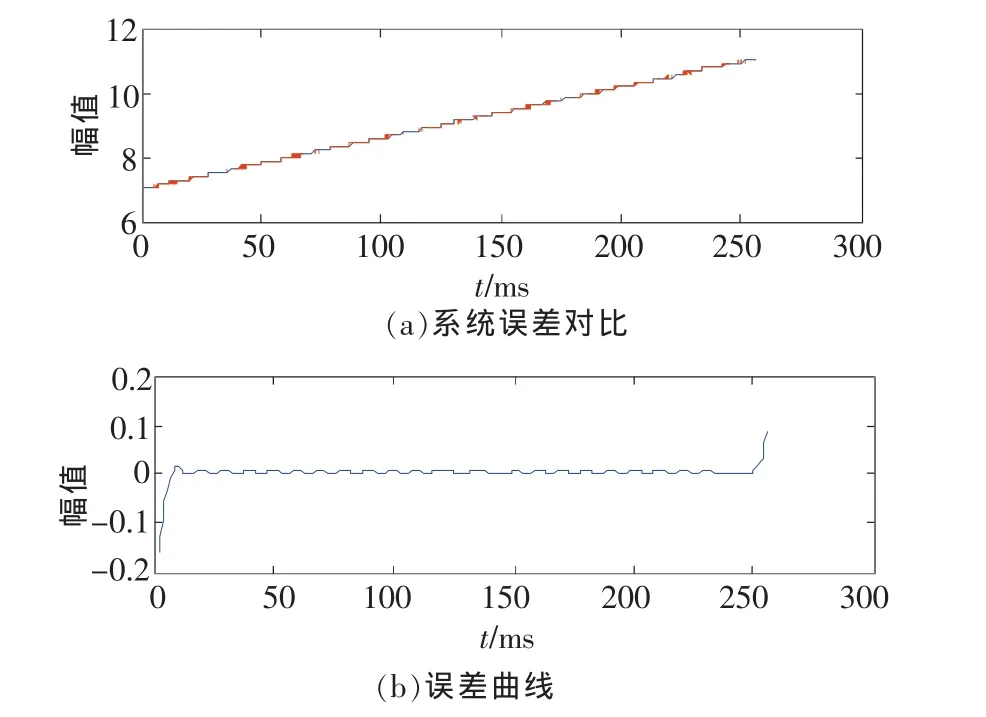
圖3 提取的系統誤差與實際系統誤差比較

圖2中，第1行為誤差x（t），第2行為100Hz的正弦分量，第3行為50Hz的正弦分量，第4行為余項，即線性變化的系統誤差。圖3給出了提取的系統誤差曲線與實際系統誤差曲線的比較及誤差曲線，圖3（a）給出了提取的系統誤差與實際系統誤差的對比，其中實際系統誤差用實線繪制，提取的系統誤差用虛線繪制。可以看到，2條曲線吻合度較高，利用EMD可以有效地提取線性變化的系統誤差。圖3（b）給出了它們的誤差曲線圖，可以看到，由于EMD算法中的端點效應[6-7]，使得數據的兩端誤差較大。

3.2 系統誤差為指數變化

系統誤差 d（t）的表達式為

對誤差x（t）進行EMD分解，其結果如圖4所示。圖5給出了提取的系統誤差曲線與實際系統誤差曲線的比較及誤差曲線。

圖4 EMD分解結果

圖5 提取的系統誤差與實際系統誤差比較

3.3 系統誤差為冪函數變化

系統誤差 d（t）的表達式為

對誤差x（t）進行EMD分解，其結果如圖6所示。圖7給出了提取的系統誤差曲線與實際系統誤差曲線比較及它們的誤差曲線。

3.4 系統誤差為大周期的周期變化

設系統誤差d（t）的表達式為

以均值為零、方差為1的正態分布白噪聲作為干擾誤差函數，對誤差x（t）進行EMD分解，其結果如圖8所示。圖9給出了提取的系統誤差曲線與實際系統誤差曲線的比較以及它們的誤差曲線。分離結果表明EMD能夠有效分離出大周期的周期性系統誤差。

3.5 系統誤差為小周期的周期變化

當周期性系統誤差比白噪聲干擾誤差函數的周期大得多時，分離效果同線性函數、指數函數、冪函數的效果相當，達到了分離要求；如若周期性系統誤差d（t）的周期與干擾誤差的周期相接近時，EMD的分離效果較差。

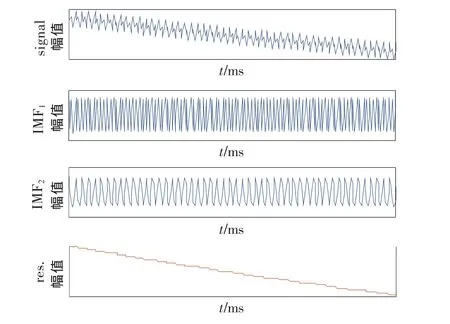
圖6 EMD分解結果

圖7 提取的系統誤差與實際系統誤差比較

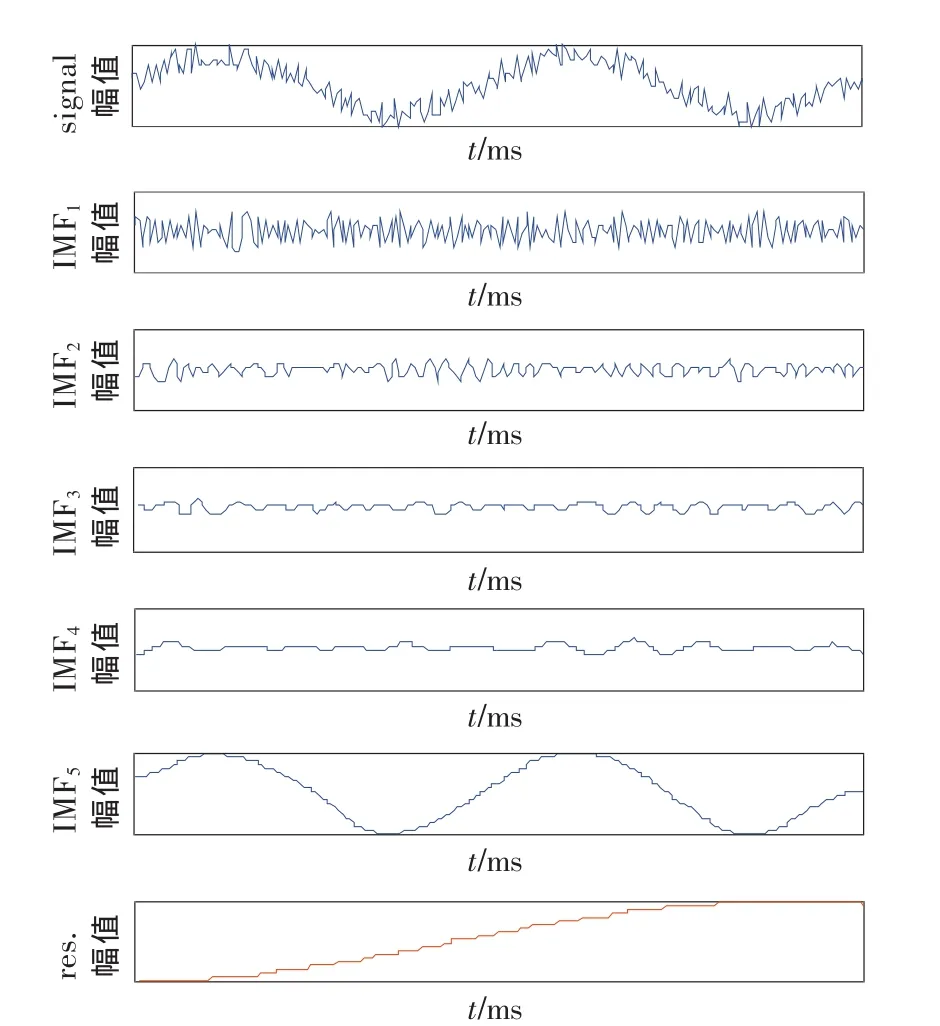
圖8 EMD分解結果

設系統誤差d（t）的表達式為

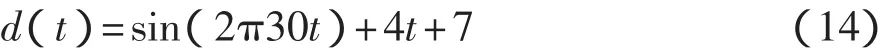
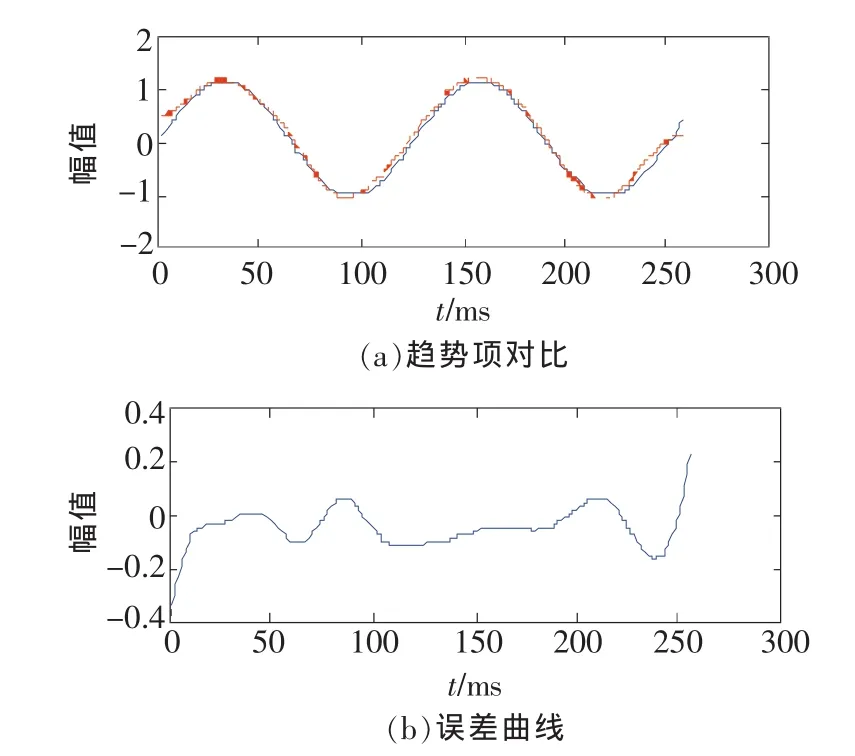
圖9 提取的系統誤差與實際系統誤差比較

圖10 誤差時域圖

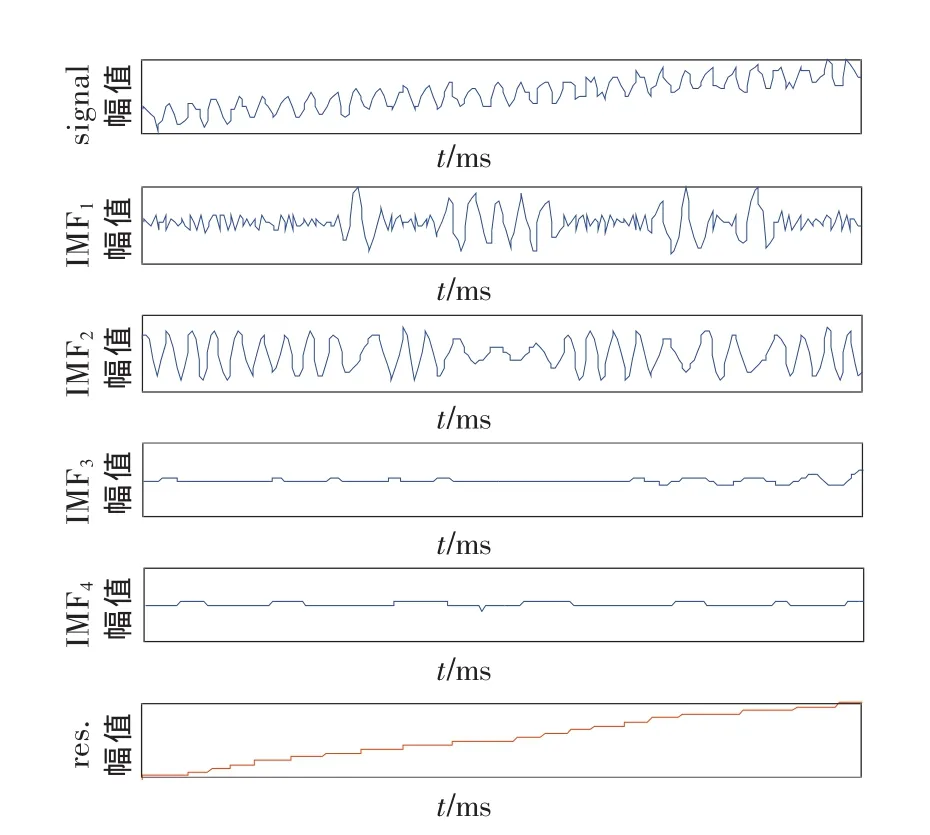
圖11 EMD分解結果

以均值為零、方差為1的正態分布白噪聲作為干擾誤差，如圖10所示。對其進行EMD分解，其結果如圖11。

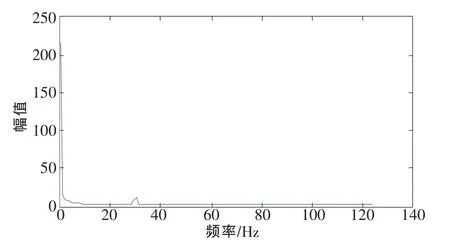
圖12 誤差頻譜

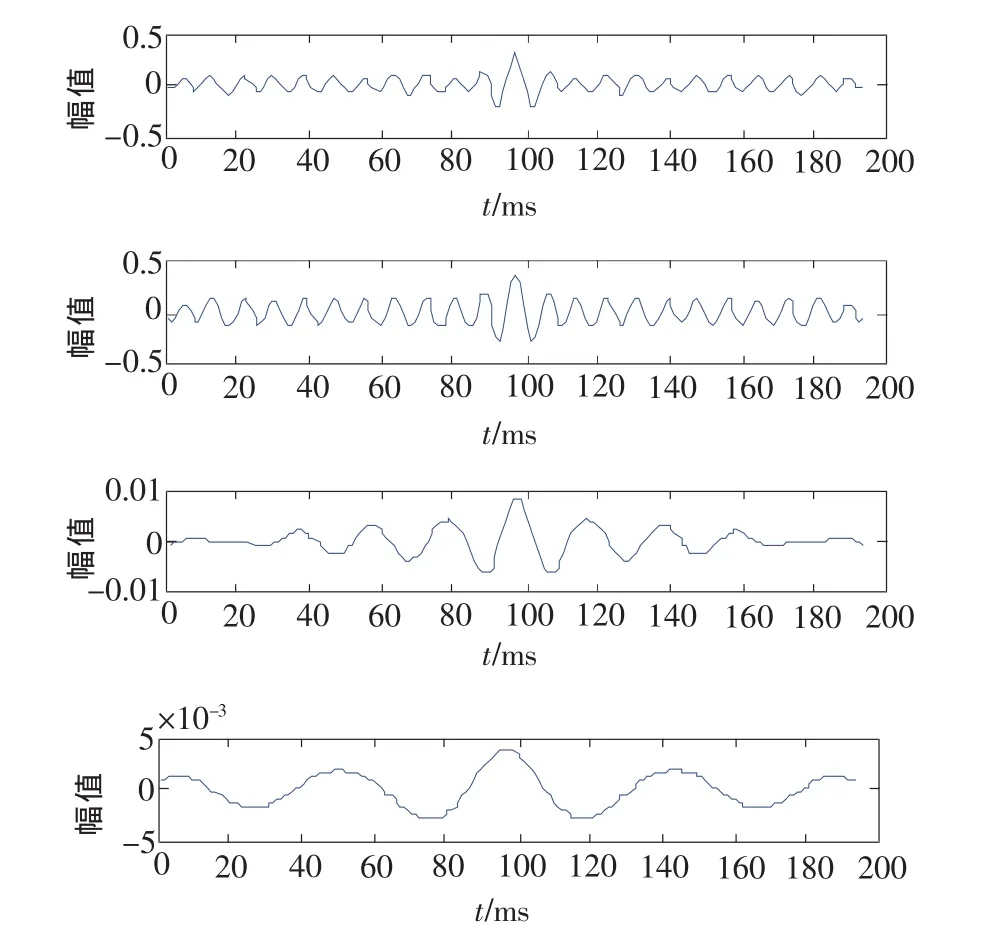
圖13 IMF的自相關函數圖

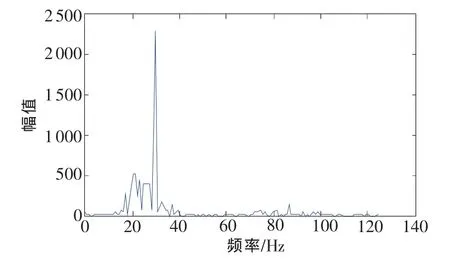
圖14 IMF1頻譜圖

圖15 IMF2頻譜圖

從圖11中可以看出，線性變化的系統誤差很容易就被分離出來，而小周期的周期性系統誤差卻很難與干擾誤差分離，且EMD的分解含有很多虛假趨勢項。由于經驗模態分解方法是依據信號時域波形極值的自適應性分解，當系統誤差的周期遠大于隨機誤差時效果顯著，如3.1～3.4；當系統誤差周期接近于干擾誤差周期時，分離效果不理想，如 3.5。

從圖11中發現，在IMF1-IMF4的時域圖中，幾乎分辨不出哪層含有周期性的系統誤差。圖12為該誤差的自相關頻域圖，能判斷出含有頻率為30 Hz的周期分量。

圖13為EMD分解后各層IMF的自相關函數圖，由上至下分別為 r1，r2，r3，r4。經過對 r1，r2，r3，r4分別作出各自的頻譜圖，可以明顯發現IMF1、IMF2兩分量中含有頻率為30Hz的周期性系統誤差，如圖14、圖15所示。

4 結束語

經驗模態分解法作為既適于線性、平穩信號，又適于非線性、非平穩信號的一種新的信號處理方法，已在許多領域得到應用。該文將經驗模態分解法運用于測量誤差數據的系統誤差分離，通過仿真驗證，該分解方法能夠有效地應用于測量誤差數據的分離，并成功地將具有不同變化特征的系統誤差進行有效提取，尤其是與自相關分析結合的經驗模態分解方法在分離周期變化的系統誤差上取得了較好的效果，為系統誤差分離提供了一種新的方法。

[1]沈國際.振動信號處理技術在直升機齒輪箱故障診斷中的應用[D].長沙：國防科學技術大學，2005.

[2] 費業泰.誤差理論與數據處理[M].北京：機械工業出版社，2004.

[3] 何正嘉，訾艷陽，張西寧.現代信號處理及工程應用[M].西安：西安交通大學出版社，2007.

[4] 陳雋，徐幼麟.經驗模分解在信號趨勢項提取中的應用[J].振動、測試與診斷，2005，25（2）：101-104.

[5] 趙海峰.基于HHT的非平穩信號故障特征提取研究[D].大慶：大慶石油學院，2007.

[6] 程軍圣，于德介，楊宇.Hilbert-Huang變換端點效應問題的探討[J].振動與沖擊，2005，24（6）：41-42，47.

[7] 胡勁松，楊世錫.EMD方法基于AR模型預測的數據延拓與應用[J].振動、測試與診斷，2007，27（2）：116-120.