基于加速度計余度配置的MEMS捷聯慣導初始對準方法

錢偉行，朱欣華，蘇 巖

（南京理工大學 MEMS慣性技術研究中心，南京 210094）

隨著MEMS慣性技術的逐步成熟，采用余度技術來提高系統精度可靠性已成為導航技術發展的一個熱點。與常規的慣性測量元件(IMU)相比，MEMS IMU具有體積小、重量輕、功耗小、成本低、動態范圍寬、響應速度快等諸多特點，而且易于安裝調試，可通過余度配置、數據融合、故障診斷與重構等方式來提高系統的性能與可靠性[1-2]。

本文針對大俯仰角條件下彈載 MEMS慣導系統初始對準中橫滾角精度低下的問題，進行了其影響因素的機理分析，提出了一種基于加速度計余度配置的捷聯慣性導航系統結構及其初始對準改進方法，并將實際系統置于高精度轉臺上，驗證了該系統結構以及初始對準方法的有效性與實際性能。

1 初始對準中橫滾角精度影響因素的力學機理分析

慣性導航系統的初始對準一般分為粗對準與精對準兩個階段。常規的粗對準方法是通過慣性傳感器敏感地球重力加速度與自轉角速度來求解慣導系統初步的水平姿態與航向信息。常規的計算公式如下：

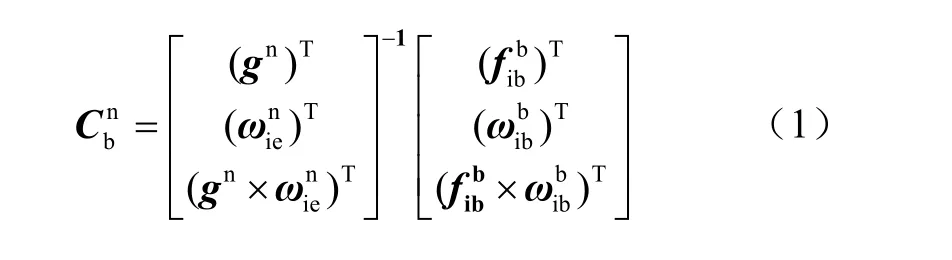
式中，gn=[0 0 -g]T為重力加速度在導航坐標系，地球自轉角速度在導航坐標系上的投影，L為當地的緯度，0ω為地球自轉角速率。近年來國內外的學者也提出過粗對準的改進方法[3]，其計算公式為：

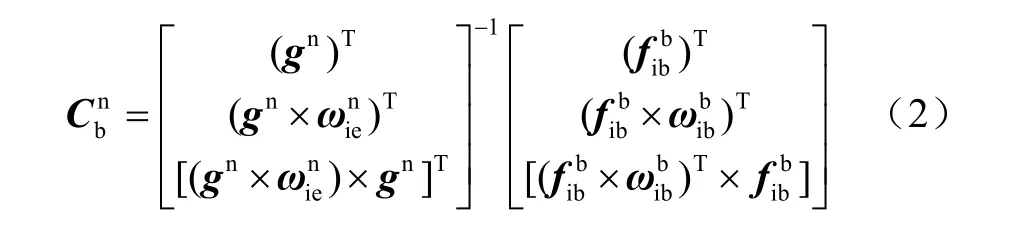
該改進方法的姿態精度相對于公式(1)有所提高，但其計算方法的物理本質是相同的。

精對準過程是采用最優估計理論方法對慣導系統的平臺誤差角以及慣性器件誤差進行實時估計與補償，從而進一步提高慣導系統的姿態精度與器件精度，航向角的對準通常采用多位置或轉動基座的方式實現[4]。

上述初始對準方法中，慣性系統通常處于水平或者接近水平的條件下進行的，而在某些特定的條件下，慣導系統必須在大俯仰角的條件下進行初始對準（如某些智能彈藥的發射環境），此時對準的橫滾角精度將一定程度上受到俯仰角的影響。

通過轉臺實驗描述該問題：將經過多位置法標定的MEMS IMU放置在某型高精度轉臺上，其精度如表1所示。控制轉臺使IMU處于不同俯仰角下，進行慣性系統的初始對準，粗對準采用公式(2)計算，精對準采用慣導線性誤差模型與卡爾曼濾波器。以轉臺作為姿態基準，不同俯仰角條件下的載體橫滾角精度如表2所示。

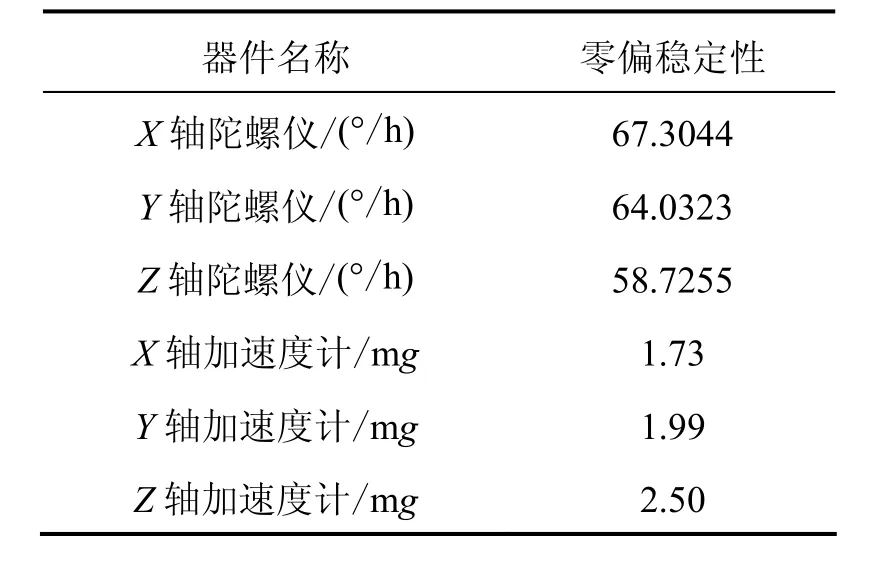
表1 MEMS慣性器件精度Tab.1 Precision of MEMS inertial instruments

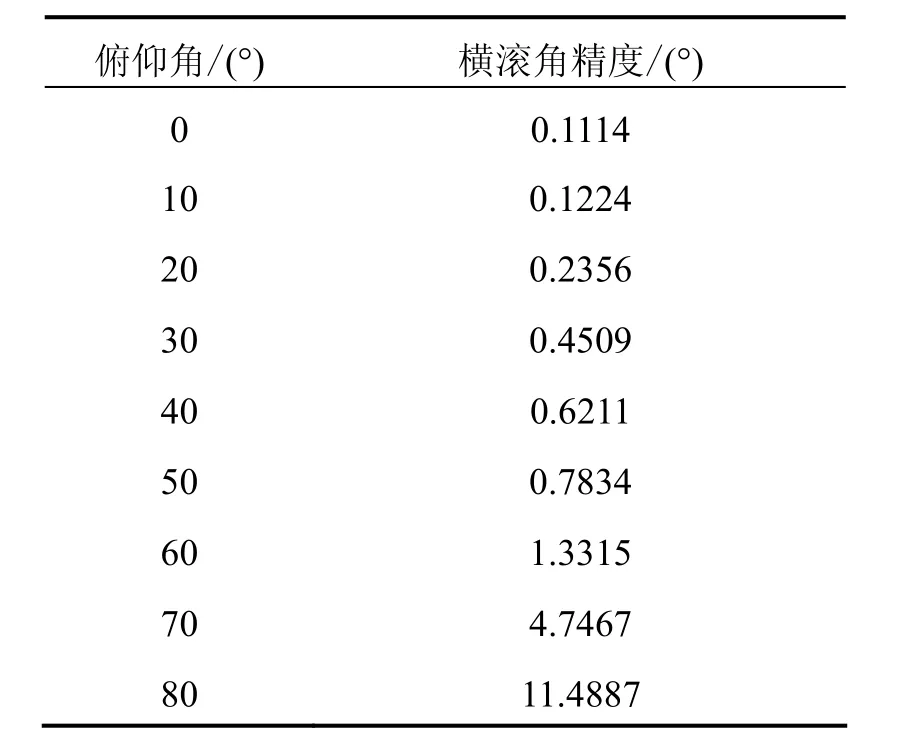
表2 初始對準中橫滾角精度與俯仰角的關系Tab.2 Relationship between precision of roll angle and pitch angle in initial alignment

由表2的實驗結果可知，隨著IMU俯仰角（即載體俯仰角）的增大，其橫滾角精度逐步下降。解決MEMS加速度計的輸出受其誤差的影響是提高對準中橫滾角精度的關鍵問題。

對初始對準中橫滾角精度受俯仰角影響的原因進行力學原理分析：在靜止載體的任意姿態條件下，重力矢量在慣導系統的載體坐標系（本文采用X、Y、Z軸分別表示右、前、上的載體坐標系）中可分解為g· s in(θ)與g· c os(θ)，其中g· s in(θ)即為載體坐標系Y軸上的加速度計所測量的重力加速度分量，如圖 1所示。

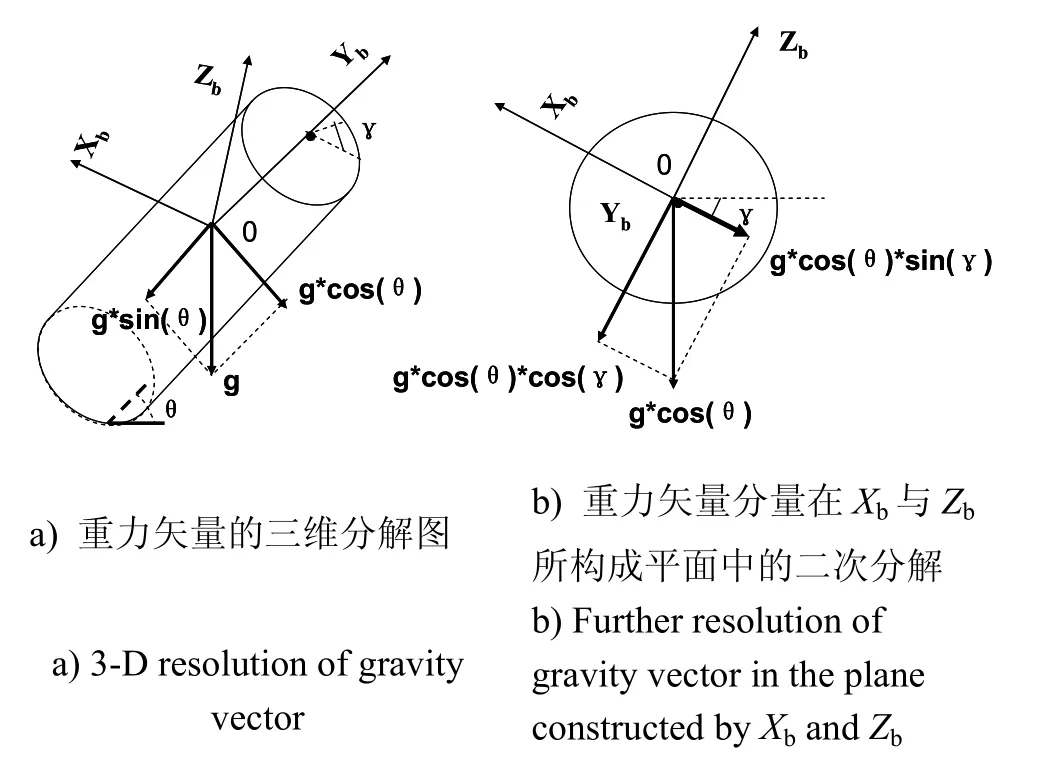
圖1 靜基座初始對準中重力矢量的分解圖Fig.1 Resolution of gravity vector in static initial alignment

將g· cos(θ)再次投影到載體坐標系X軸與Z軸上，即可分別得到該兩軸上加速度計的測量值g·co s (θ)·sin(γ)與g·co s (θ)·co s (γ)，初始對準即通過這兩個重力矢量的分量來的敏感載體的橫滾角。由于這兩個分量的絕對值將隨著俯仰角的增大而減小，因而在大俯仰角的條件下受到加速度計噪聲的影響較大。

對于MEMS慣導系統，其加速度傳感器目前的精度一般處于毫g級別，在大俯仰角的條件下g·cos(θ)·sin(γ)與g·co s (θ)·co s (γ)受到器件誤差的影響較石英撓性等類型的加速度計更為明顯，即表 2中所示的情況。

2 基于加速度計余度配置MEMS捷聯慣導系統結構設計

針對上述問題，可對慣導系統的結構采用余度配置方案。文獻[3][4]提出了基于6個單軸MEMS陀螺儀與6個單軸MEMS加速度計的正十二面體余度配置方案，該方案對于慣性器件安裝面的加工有特殊的要求，并且系統須完成特定的標定過程。

本文提出了一種在常規捷聯慣導系統結構上進行3軸加速度計斜裝余度配置的系統結構改進方法，即在常規的MEMS IMU結構（包含3個相互正交的陀螺儀和3個相互正交的加速度計）的基礎上，增加3個斜裝且相互正交的加速度計，其三軸分別定義為X’b、Y’b與Z’b，如圖 2 所示，其中 MEMS IMU 與 3軸余度配置的加速度計已經過多位置法等方式進行標定，標定過程本文不再詳述。

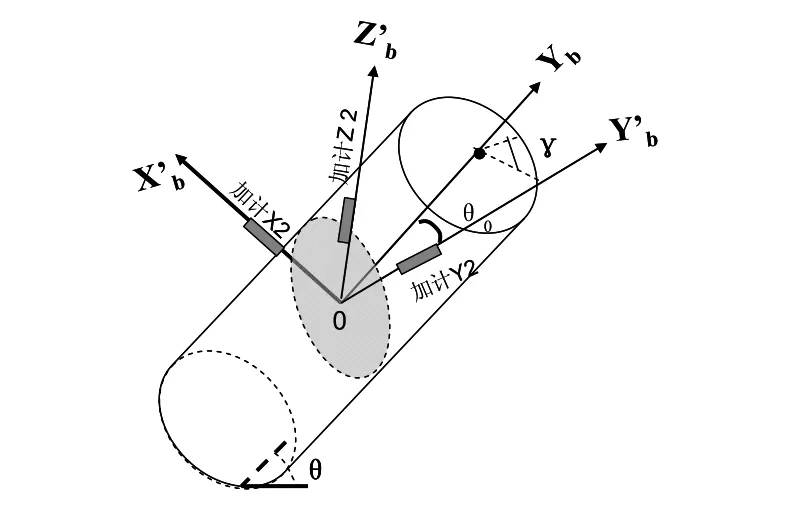
圖2 慣導系統的加速度計余度配置示意圖Fig.2 Accelerometer redundant configuration of inertial navigation system

該余度配置的結構中，斜裝的X’b、Z’b軸處于與原系統結構中X軸與Z軸所構成的平面成0θ夾角的平面內，即圖中以灰色表示的平面，Y’b軸垂直于該平面，因此Y’b與Yb之間的夾角為0θ。X’b、Y’b、Z’b之間構成右手直角坐標系。系統結構上的余度配置部分可視為3軸加速度計相對于常規IMU的整體斜裝。在載體靜止、橫滾角為γ、俯仰角為θ的狀態下，余度配置的三軸加速度計的理想輸出為：

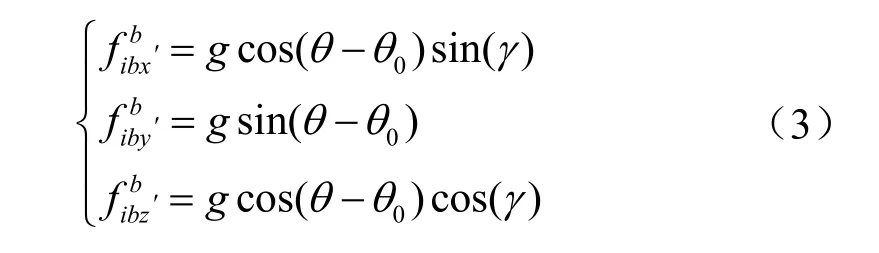
當系統在大俯仰角（如接近 90o）下啟動時，的位置啟動時，則 (θ-θ0)仍處于常規的俯仰角范圍（若取θ0為45o，則(θ-θ0)接近 45o），即便采用 MEMS加速度計，的值也將遠大于加速度計的噪聲數量級。通過公式（4）即可初步獲得載體的橫滾角，再將該橫滾角作為精對準的初始姿態角。

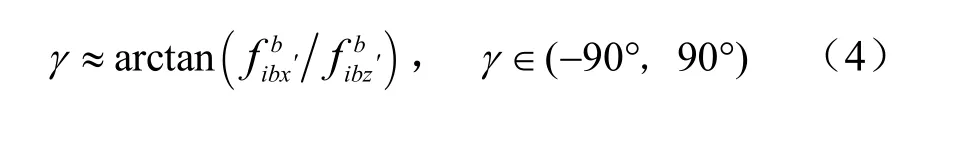
因此，利用該余度配置方案可有效提高慣導系統初始對準與導航定位的性能。

3 基于加速度計余度配置的初始對準改進方法

3.1 余度配置加速度計等效比力的計算

上節提出的基于加速度計余度配置的 MEMS捷聯慣導系統，可實現全俯仰角范圍（-90o～90o）內精確的初始對準，為了便于說明，本文中暫定義橫滾角范圍為-90o～90o，俯仰角與航向角的范圍與常規的捷聯慣導系統一致。根據圖1中表示的載體坐標系下3軸加速度計度計的輸出，以及公式（3）中余度配置的 3軸加速度計的輸出，可通過三角函數關系得到將余度配置的加速度計輸出投影到載體坐標系中的公式，如公式（5）所示：

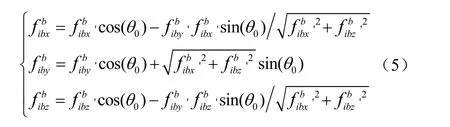
由此可將余度配置的加速度計輸出等效為載體坐標系下的加速度計輸出。

3.2 自適應加權最小二乘加速度計數據融合

相關研究表明，兩個互不相關的時間序列，其隨機噪聲滿足白噪聲特性，則兩個時間序列加權平均值的誤差均方根小于其中任意一個序列[5]。隨機信號的該特性已被運用于慣性傳感器的信號處理。本文通過自適應加權最小二乘算法，利用IMU中加速度計輸出與余度配置加速度計輸出進行數據融合，提高比力的零位偏置穩定性。自適應加權最小二乘基本原理及算法推導過程詳見文獻[5]，由于篇幅限制本文將不再贅述。

3.3 初始對準改進方案

基于上述分析，提出一種基于加速度計斜裝余度配置的MEMS慣導系統初始對準方案。對準流程如圖3所示。

該方案與常規對準方案的步驟類似，分為粗對準與精對準兩個步驟：

1）粗對準過程中通過常規IMU加速度計輸出初步判斷載體的俯仰角，若超過一定閾值（如 40o）則采用余度配置加速度計的輸出求解橫滾角，并根據IMU加速度計與余度加速度計輸出的偏置穩定性確定加權最小二乘算法的初步權值，同時通過陀螺儀靜態輸出求解其常值零偏；

2） 精對準過程中根據余度配置加速度計輸出計算其等效比力值，通過加權最小二乘算法進行數據融合，其權值根據實測比力的偏置穩定性在線調整，將融合后的比力與經常值零偏補償后陀螺儀數據進行捷聯慣性導航解算以及最優濾波估計，完成精對準；

在此特別說明，由于MEMS陀螺儀精度較低，且靜態初始對準無法精確估計航向誤差角，因此對準過程中的航向信息通過外觀測方式獲得。

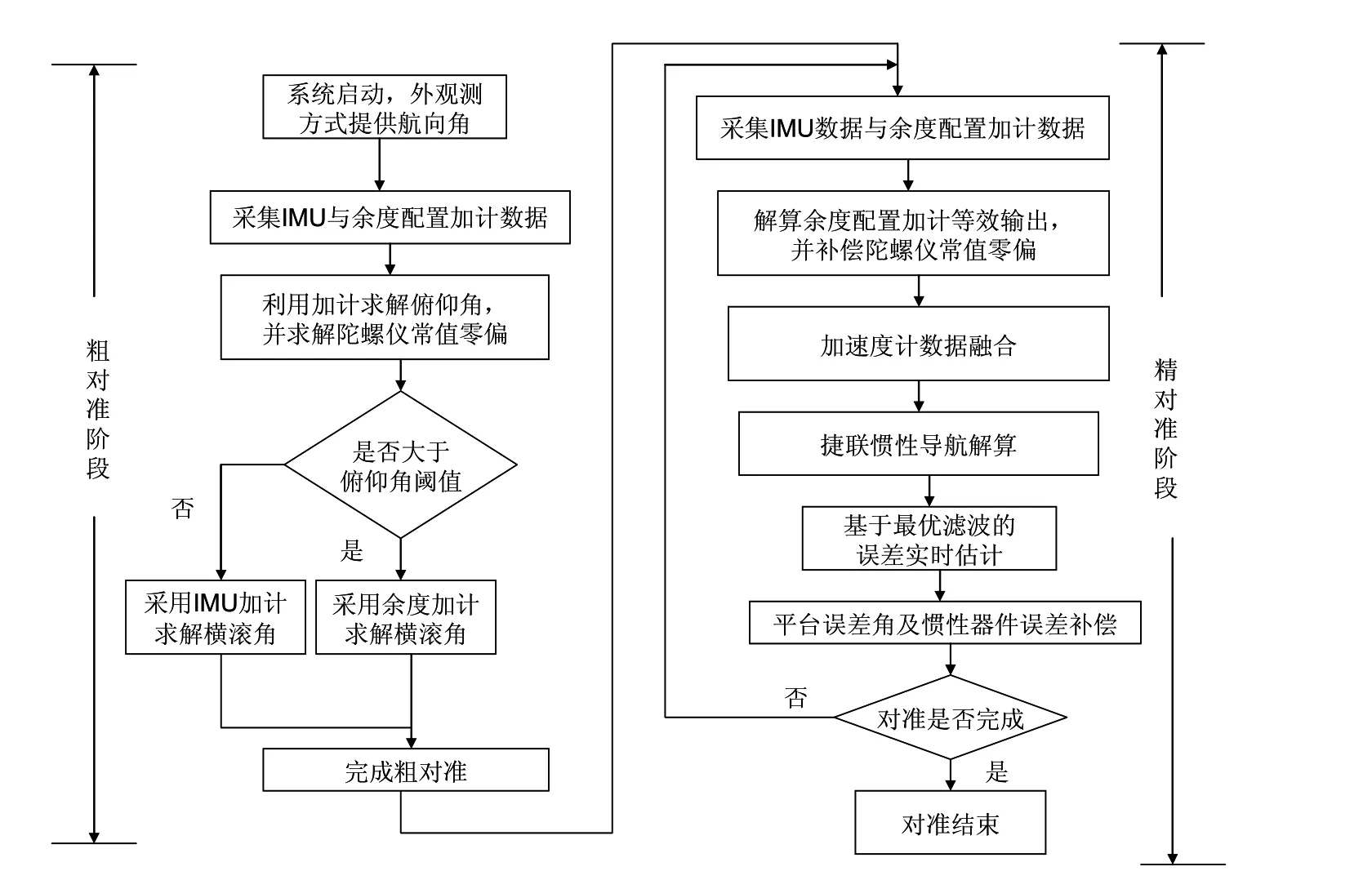
圖3 基于加速度計余度配置的初始對準改進方案Fig.3 Improved scheme of initial alignment based on accelerometer redundant configuration

4 實驗驗證與性能特點分析

4.1 余度配置MEMS慣導系統的對準性能驗證

按本文第2節所示方法構建基于加速度計余度配置的MEMS慣性傳感器結構，斜裝角度0θ取為40o（為保證系統在完整的俯仰角定義域內的對準精度，0θ宜設置在40o～50o），并研制了基于DSP5416的導航計算機，在某型高精度位置速率轉臺上進行上述初始對準改進方法的試驗驗證。試驗中載體俯仰角由轉臺控制由0o逐步增大到80o，間隔為10o。粗對準與精對準過程按如圖3的所述時序進行。

實驗中IMU的慣性傳感器配置如表1所示，余度配置加速度計與IMU加速度計采用相同的型號。圖4為載體俯仰角 80o條件下數據融合前后的比力值對比，其中深色曲線為經過融合的數據輸出，淺色曲線為IMU中加速度計的輸出。由于其他俯仰角條件下的數據融合結果類似，本文不再展開。

理論上，滿足加權最小二乘條件的兩個相同型號的傳感器，數據融合后的均方差為傳感器均方差的。由圖 4可知，采用自適應加權最小二乘算法后，載體坐標系X軸與Y軸加速度計的零位偏置穩定性由2.0 mg左右降低到1.5 mg左右，Z軸加速度計的零位偏置穩定性由2.5 mg左右降低到2.0 mg左右，略大于理論計算值，但基本相當。

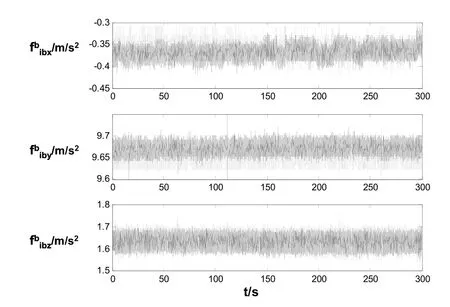
圖4 數據融合前后加速度計輸出對比Fig.4 Comparison of the output before and after data fusion

改進初始對準方法中俯仰角與橫滾角精度的關系如表3所示，表中分別列出了采用加速度計數據融合后的對準精度，以及直接采用IMU加速度計進行對準后的精度。

對比表1與表3可知，載體俯仰角在40o以下時，常規對準方法與余度配置改進方法的橫滾角精度相當，在俯仰角超過40o時，改進方法的橫滾角誤差較常規對準方法有顯著提高；對比表3中采用加速度計數據融合前后的對準結果可知，相同俯仰角條件下，加速度計數據融合后的橫滾角精度，相對于直接采用IMU加速度計有所提高，實驗證明了提高慣性傳感器的零偏穩定性可有效提高初始對準的精度。

表3 初始對準改進方法中橫滾角精度與俯仰角的關系Tab.3 Relationship between roll angle precision and pitch angle in improved initial alignment scheme

4.2 余度配置MEMS慣導系統性能特點分析

本文提出了一種基于 3軸加速度計斜裝余度配置的捷聯慣導系統，該系統具有如下性能特點：

1）相對于文獻[6]與[7]所提出的基于正十二面體結構的余度配置MEMS慣導系統，本文所提出的系統結構是基于常規捷聯慣導系統的改進結構，慣性傳感器組件的選型、裝配與標定過程也更接近常規的捷聯慣導系統，更適合于二維彈道修正彈藥、微型飛行器等應用環境；

2） 本文所提出系統結構在大俯仰角下的對準精度主要取決于以下幾個方面：①慣導系統誤差模型的準確性；②最優濾波器的選擇；③慣性器件誤差特性及其標定精度；④斜裝加速度計的安裝面加工精度。

3） 對于捷聯慣性導航系統結構，本文提出的改進方案可視為由兩組相互獨立的3軸正交加速度計組件，以及一組3軸正交陀螺儀組件構成，兩組加速度計組件可與陀螺儀組件分別構成兩套完整的IMU（其中一套可視為加速度計斜裝慣導系統[8]），可通過故障診斷與隔離功能算法提高系統的性能與可靠性。

5 結 論

本文以MEMS慣性導航系統為研究背景，研究了一種基于三軸加速度計斜裝余度配置的慣導系統結構，以及在載體大俯仰角條件下精確估計其橫滾角的初始對準方法。論文分析了常規對準方法在大俯仰角條件下無法精確估計橫滾角的物理本質，針對該問題提出了加速度計余度配置改進方案，并論證了改進方案在提高橫滾角估計精度上的有效性。高精度轉臺上的實驗驗證表明，對于大俯仰角下啟動的MEMS捷聯慣性導航系統，本文所提出的余度配置方案可有效提高橫滾角估計精度以及加速度計零偏穩定性，并使系統具有故障診斷與隔離的功能，對MEMS慣性導航系統在彈載環境中的工程應用具有較為重要的參考價值。

（References）：

[1] Seong Yun Cho, Chan Gook Park. Calibration of a redundant IMU[C]// AIAA Guidance, navigation, and Control Conference and Exhibit, 2004: 5114-5123.

[2] Park S, Tan C W, Park J. A scheme for improving the performance of a gyroscope-free inertial measurement unit[J]. Sensors and Actuators A: Physical, 2005, 121:410-420.

[3] Jamshaid A, Fang Jiancheng. In-flight Alignment of inertial navigation system by celestial observation technique[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2005, 22(2): 132-138.

[4] Ishibashi S, Tsukioka S, Yoshida H, et al. Accuracy improvement of an inertial navigation system brought about by the rotational motion[R]. Japan Agency for Marine- Earth Sci & Technol. (JAMSTEC), Yokosuka,2007: 1-5.

[5] 楊叔子，吳雅，軒建平，等. 時間序列分析的工程應用[M]. 武漢：華中科技大學，2007.YANG Shu-zi, WU Ya, XUAN Jian-ping, et al. The engineering application of time series analysis[M].Wuhan: Huazhong University of Science and Technology,2007.

[6] HUA Bing, LIU Jian-ye, LI Rong-bing, et al. A study on turning calibration technology of MEMS-SINS with redundant configurationp[J]. Journal of Astronautic, 2009,30(2): 468-473.

[7] 蘆佳振，張春熹，祝露峰. 余度捷聯慣導系統連續自動標定技術[J]. 北京航空航天大學學報，2009，35(3)：366-370.LU Jia-zhen, ZHANG Chun-xi, ZHU Lu-fen. Technique of continuous auto-calibration of redundant strapdown inertial system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(3): 366-370.

[8] 華冰，劉建業，孫永榮. 彈道導彈IMU斜裝余度配置設計的系統性能分析[J]. 兵工學報，2007，28(10)：1209-1213.HUA Bing, LIU Jian-ye, SUN Yong-rong, Performance analysis in a ballistic missile IMU system with skewed redundant configuration[J]. Acta Armamentarii, 2007,28(10): 1209-1213.