基于ANSYS對罐體垂向載荷施加方法研究*

楊亮亮,傅茂海,安 琪,邵朋朋

(西南交通大學 機械工程學院,四川成都610031)

罐車是一種車體主要結構呈罐形的車輛,用來裝運各種液體、液化氣體及粉末狀貨物等,其罐體屬于運動中的壓力容器。設計滿足壓力容器相關標準、結構強度和輕量化要求的罐車罐體是保證運輸安全和降低成本的前提。其中如何模擬罐體垂向載荷的施加方法對設計階段準確評估產品的性能有著至關重要的影響。由于罐車內的貨物和罐體之間存在接觸問題,所以有限元模型中載荷的施加變得比較復雜。為了能夠方便而準確的利用ANSYS對罐體進行有限元計算分析,一般在分析模型中采用如下幾種方法對罐體垂向載荷進行模擬:

(1)直接將貨物重力的影響等效為作用在罐體下半部分內壁面的垂向均布壓力,忽略罐體本身幾何形狀的影響。

(2)等效分割法。將罐體內的貨物沿縱向切分成若干部分,通過數值方法把每一部分質量換算為該處承載面的垂向載荷,即對罐體下半部分施加垂向非均布載荷。

(3)耦合自由度法。建立質量單元和接觸對,通過節點自由度耦合來模擬貨物和罐體內壁的接觸。

(4)考慮貨物和罐體接觸面相互作用的影響,以接觸單元為主,綜合線性彈簧—阻尼單元,建立結合面的有限元模型,若裝載貨物為流體,需采用合理的流體單元模擬[1]。

以上幾種方法中,第(1)種方法簡單,但模型簡化較粗糙,會造成局部應力分析的結果與實際差別很大;第(2)種方法相對第(1)種方法模型簡化有所改進,但其分析結果的精度與承載面分割的份數有直接關系;第(3)種方法有較高的精度,通過簡化的質量單元達到了將非線性問題的線性化,但是這(3)種方法都忽略了貨物和罐體的結合面效應;第(4)種方法就是包含結合面效應的方法[2],該方法理論上比較完善,但屬于非線性問題,計算復雜耗時,一些參數又需要試驗測定,并且測定比較難。

針對以上方法的特點,采用了等效分割和耦合自由度法兩種方法來對比驗證其合理性。分析結果證明,這兩種方法有較高的計算效率和計算精度,對模擬罐體垂向載荷可以提供一定參考價值。

1 罐體垂向載荷施加方法的研究

如上所述,采用等效分割與耦合自由度兩種方法能夠方便而比較準確的利用ANSYS軟件進行計算分析,下面就這兩種方法在ANSYS模型中的應用進行分析。

1.1 等效分割法

該方法是將罐體內的貨物沿縱向切分成若干部分,并把每一部分質量換算為該處承載面的垂向載荷,即對罐體下半部分施加垂向非均布載荷。具體方法如圖1所示的3組貨物分割模型,這里假設貨物頂部處于水平狀態。其中圖1(a)是將貨物按照罐體的幾何形狀沿著縱向等距切分成6份的簡化模型,圖1(b)和圖1(c)依次將貨物分割成12份和24份,倘若將貨物無限切分下去就成為了圖1(d)中的模型,這也是實際情況下的貨物裝載效果圖。

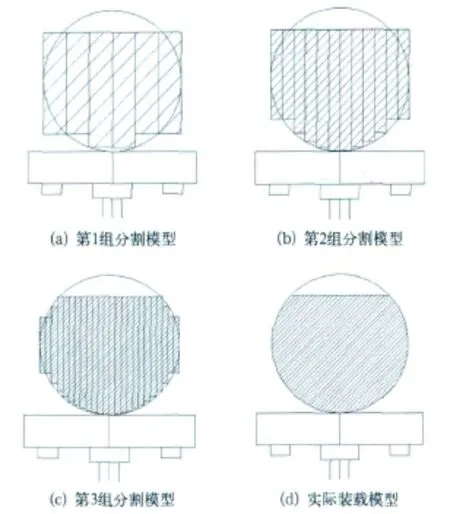
圖1

由于研究的工況基本都屬于靜態或準靜態載荷工況,而且罐體的幾何形狀是對稱的,此情況下切分后的貨物之間產生的相互影響可以忽略,這為建立的等效分割模型的合理性提供了一定的依據。通過計算得出每一份貨物質量作用于相應罐體承載面的垂向壓力。

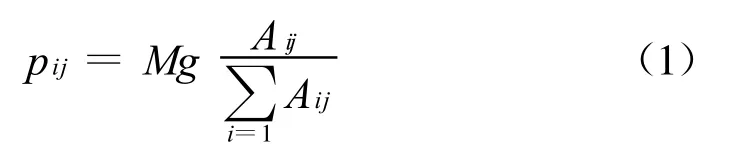
式中i表示份數;j表示組數;M表示貨物總質量;Aij表示第j組第i份貨物斷面面積;g表示重力加速度。i的值越大,罐體承載面所作用的等效垂向壓力的分布就越均勻。此外,還需要考慮罐車車體自身的重力以及罐內氣體壓強的影響。

1.2 耦合自由度法

由于罐體和罐裝貨物之間存在接觸問題,是一種高度非線性行為,盡管模擬出罐體和貨物之間結合面效應可以使模型的計算結果更精確,但是計算成本很大。在ANSYS模型中,如果不考慮摩擦,且物體之間總是保持接觸,則可以應用約束方程或自由度耦合來代替接觸。如果建立約束方程[3],則必須滿足:

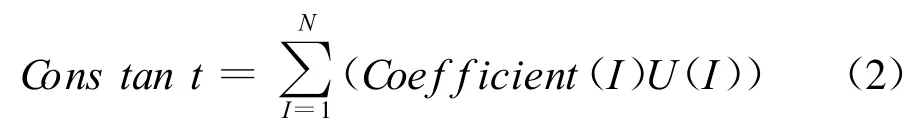
式中U(I)是自由度項,一般包括3個平動和3個轉動自由度;N是方程中項的編號。約束方程迫使這些自由度之間取得線性的關系。

而耦合自由度就是建立一個耦合設置,使其被約束在一起,并具有相同的自由度。但是耦合的應用必須具備下列4個條件[4]:

(1)表面保持接觸;(2)小變形分析;(3)忽略摩擦;(4)在兩個界面上,節點是一一對應的。

顯然,對于罐體垂向載荷的分析可以滿足以上4個條件,因此利用耦合自由度方法來模擬接觸面是合理可行的,并使分析簡化為線性問題,大大節約計算資源和時間。

假設貨物的密度是均勻分布,為了要確定貨物重心位置,只需要找到貨物形心位置,建立如圖2所示的罐體斷面模型。

圖2 罐體斷面計算模型

取對稱軸為y軸,則形心必位于該軸上,再在距z軸為任意高度y處取平行于z軸的微面積dA,則貨物斷面積相對于z軸的面距為:

式中R為罐體半徑;h為貨物裝載高度。設斷面形心C的坐標為yC,則:

然后將罐體內的貨物在其重心位置處用質量單元來代替,且賦給實際貨物的相關屬性,并將質量單元和罐體承載面進行耦合自由度,建立接觸對來模擬貨物對罐體的影響。

2 計算實例

2.1 有限元模型的建立

以某有底架罐車車體為對象,用ANSYS軟件建立其有限元分析模型。

罐車車體主要由罐體和底架等組成。罐體由筒體、封頭、鞍座、防波板等零部件組焊而成。筒體半徑1 104 mm,厚度8 mm;封頭為球形封頭,厚度10 mm。底架主要由中梁、枕梁、端梁及側梁等部分組成。罐體中部的上鞍與底架中部的下鞍用螺栓進行連接,同時罐體落于枕梁鞍座處。利用ANSYS有限元分析軟件建立模型并離散[5],整個罐車車體鋼結構共劃分為78 200個節點,65 880個板殼單元。在上心盤處施加邊界條件,邊界條件采用彈性體邊界元處理,其剛度參照轉向架的懸掛剛度,整車共有24個邊界元。車體的有限元模型如圖3所示。

圖3 罐車車體有限元模型

2.2 載荷工況的計算

按照有關標準和技術條件的要求,對該罐車車體鋼結構進行有限元靜強度分析計算時考慮以下幾種載荷情況:

工況Ⅰ:垂向靜載荷+自重+0.28 MPa罐內壓力;

工況Ⅱ:(垂向靜載荷+自重)×1.6+0.28 MPa罐內壓力+150 t縱向拉伸力;

工況Ⅲ:(垂向靜載荷+自重)×1.6+0.28 MPa罐內壓力+150 t縱向壓縮力;

工況Ⅳ:垂向靜載荷+自重+0.28 MPa罐內壓力(頂車工況)。

罐車車體鋼結構為板材拼組的焊接結構。板材或者型材材料采用Q345高強度低合金結構鋼。沖擊座的材質為C級鑄鋼。根據該罐車技術條件規定,罐車車體應在各個加載的載荷綜合作用下,當量應力應不大于材料的屈服極限(345 MPa)。當量應力按下列公式計算:

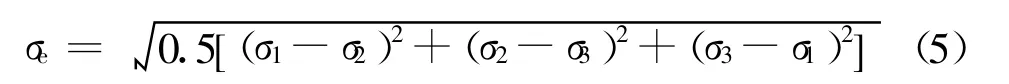
式中 σe為當量應力,MPa;σi為主應力(i=1,2,3),MPa。

2.3 計算結果對比與分析

采用不同的垂向載荷處理方法,4種載荷工況中罐體的最大應力分析結果見表1,在表1中,以耦合自由度法計算結果為基準值,計算其他方法計算結果的相對誤差。

從表1中可以看出,最大應力主要發生在罐體與防波板連接處和罐體與鞍座連接處,與實際是相吻合的。各組合工況下的最大應力均小于其許用應力,滿足標準要求。對于工況Ⅱ和Ⅲ中出現最大應力發生位置不一致的情況,是由于將貨物分割成圖2(a)和圖2(b)時,靠近罐體和防波板連接處的那部分貨物質量偏大,于是該處等效的承載面受力也偏大,從而導致了部分組合工況下局部應力的差異。

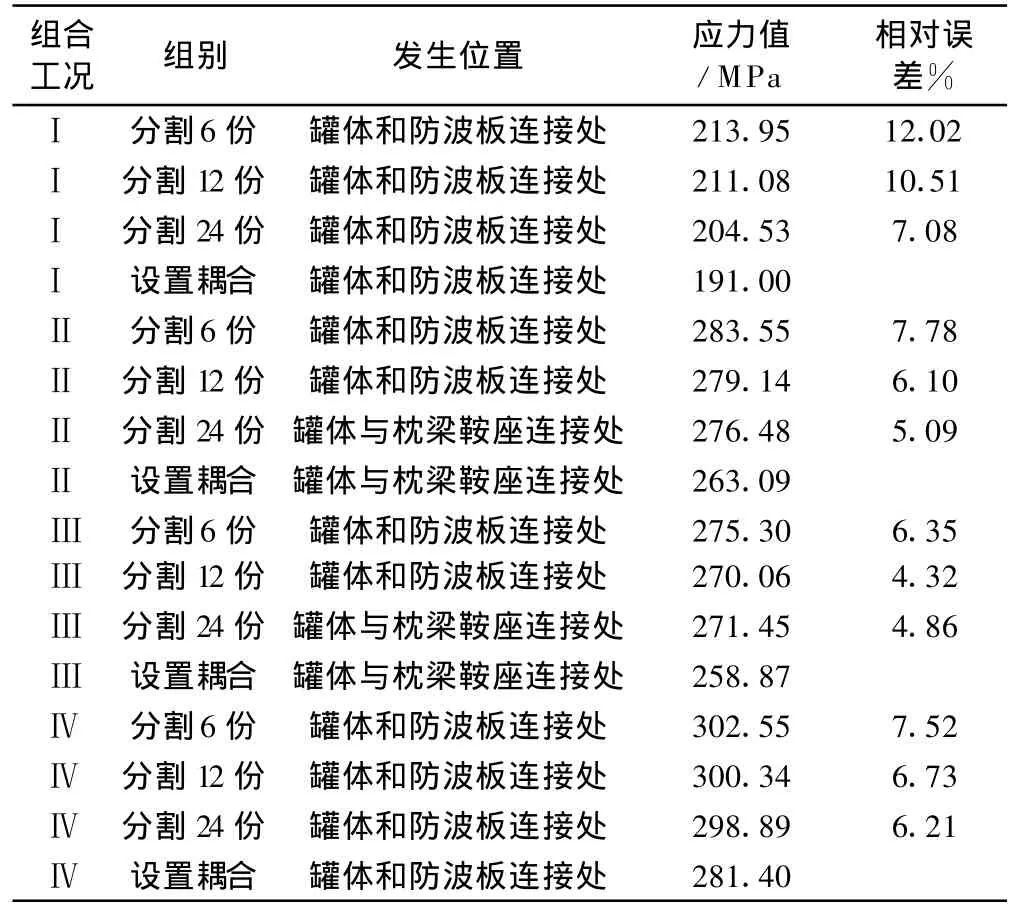
表1 最大等效von_Mises應力及其位置

圖4 垂向靜載荷工況下等效von_Mises應力云圖

為了更好的比較分析等效分割法與耦合自由度法兩種方法的準確性,下文分析了在垂向靜載荷工況下的計算結果,從而能更直觀的看到不同罐體垂向載荷施加方法對罐體結構的強度和剛度影響。

圖4為垂向靜載荷工況下的等效von_Mises應力云圖,其中圖4(a)、圖 4(b)、圖4(c)和圖4(d)分別代表分割6,12,24份和耦合設置4組情況,從圖中可以看出其最大應力區域的應力分布基本相同,并且整體應力分布呈現逐漸逼近的趨勢。

圖5為垂向靜載荷工況下部分區域最大節點應力統計曲線圖。其中第1組曲線為利用耦合自由度法得到的垂向靜載荷工況計算結果,提取了罐體結構中10個關鍵區域處的節點最大應力值,其中節點1～4在罐體和防波板連接處;5～8在罐體與枕梁鞍座連接處;9和10在罐體球形封頭過渡處。并利用等效分割法將這10個節點在分割6,12,24份情況下的應力值分別列出,即圖5中第2,3和4組所示。

從圖5可以看出,在罐體和防波板連接處以及球形封頭過渡處,用等效分割法計算的應力結果比耦合自由度法的計算結果大;而在罐體與枕梁鞍座連接處,用等效分割法計算的應力結果比耦合自由度法的計算結果小,但是4組結果的相對誤差不大。同時可以看出,分割的份數越多,計算結果就越接近耦合方法的計算結果,說明耦合自由度方法較等效分割法更準確。

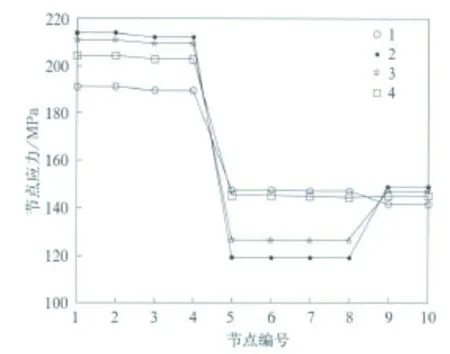
圖5 部分節點應力在各組情況下的應力值

圖6為垂向靜載荷工況下的罐體位移變形圖,其中圖6(a)、圖6(b)、圖6(c)和圖6(d)分別代表分割6,12,24份和耦合設置4組情況,從罐體中心斷面處觀察可以看出其位移變形基本一致,也呈現逼近趨勢。

3 結論

(1)用等效分割法模擬罐車貨物對罐體的影響,基本可以準確地得到罐體的整體位移和應力分布。隨著分割份數的增加,局部位移和應力的分布會更精確。

(2)用耦合自由度法來模擬貨物和罐體的接觸面,使接觸非線性問題變成線性問題,不僅大大節約計算資源,并且能準確的得到整體和局部的計算結果,更與實際相吻合,且載荷施加更加方便。

圖6 垂向靜載荷工況下的罐體位移變形圖

(3)通過對罐車罐體垂向載荷施加方法的探討和計算實例的對比驗證,兩種方法分析結果在罐體強度和剛度上都基本一致,均能滿足一般工程應用的要求,對鐵路罐車車體的結構分析有一定的參考價值。

(4)對于如黏油罐車等而言,貨物與罐體之間的摩擦力可能相對較大,如果貨物和罐體的結合面效應對研究對象的影響不能忽略,就需要利用有限元方法建立接觸單元進行非線性分析,并考慮試驗條件下的摩擦系數、黏性系數等貨物材料特性。

[1] 趙 勇,張若京,孫利民.G70B列車油罐液固耦合模態分析[J].計算機輔助工程,2007,16(3):119-122.

[2] 秦緒柏,陳 南,等.耦合結點子模型法在螺栓聯接結構分析中的應用[J].精密制造與自動化,2003,153(1):32-33.

[3] 黃明高,姚曙光.耦合與接觸非線性在鐵道罐車車體結構分析中的應用[J].鐵道機車車輛,2007,27(6):23-26.

[4] 傅茂海,安 琪,楊亮亮.出口孟加拉國罐車車體強度報告[R].重慶長征重工有限責任公司,2010.

[5] 嚴雋耄,傅茂海.車輛工程(第 3版)[M].北京:中國鐵道出版社,2008.

[6] 王勖成,有限單元法[M].北京:清華大學出版社,2003.