壓氣機葉片最大撓度相對位置對顫振影響的數值研究

陸慶飛

(中國燃氣渦輪研究院，四川 成都 610500)

1 引言

葉片顫振是流動誘發的自激振動，其觸發機制與葉片的結構參數和振動葉片的非定常流動狀況緊密相關。隨著航空發動機向高推重比方向發展，在級負荷增大、葉片相對厚度減小、部件剛性下降等因素的影響下，葉片顫振故障頻發，已成為高性能航空發動機研制過程中急需解決的挑戰性問題。葉片顫振故障常常造成災難性的后果，而解決故障要耗費大量的人力、財力。

目前，預測葉片顫振的方法一般有三類：經驗法、半經驗法和計算流體力學法(即能量法)。經驗法通過大量的試驗來建立葉片顫振數據庫；半經驗法從流體力學的基本方程組出發，同時又引入工程試驗數據。本文采用的是計算流體力學法，該方法能準確捕捉到葉片表面的壓力分布和激波振蕩，有助于了解葉片的顫振機理，逐步積累葉片顫振的數據，適合工程應用[1]。

2 計算方法簡介

以結構動力學方法(用ANSYS軟件)確定葉片振型、自振頻率和振幅分布后，假設葉片作簡諧振動，得出葉片結構運動方程(體現在網格的運動規律上)。然后將這種位移規律納入振動葉片的非定常流場數值模擬中，計算葉片上的非定常氣動力及氣動力所做的功，最后采用能量法來評估顫振發作的幾率。能量法采用能量的觀點來建立氣動彈性穩定性判別原則。當葉片由于某種原因產生振動時，會與周圍的氣體發生能量交換，如果葉片向氣流傳遞能量，即非定常氣動力對葉片做負功，則葉片振動將會衰減；反之，如果葉片從氣流中吸收能量，非定常氣動力對葉片做正功，則葉片振動會加劇。在忽略機械阻尼時，以一個振動周期內葉片與周圍氣體吸收能量的正負關系來判斷葉片是否顫振，此即本文使用的能量法判定準則[2]。

3 動葉振動分析

取某型壓氣機第一排轉子為研究對象，通過改變造型參數來調節葉片的最大撓度相對位置(分別標為 1，2，3，4，造型參數見圖 1)，其他參數基本不變。葉片由鈦合金制成，其材料特性為：彈性模量119 GPa，泊松比 0.33，密度 4480 kg/m3。

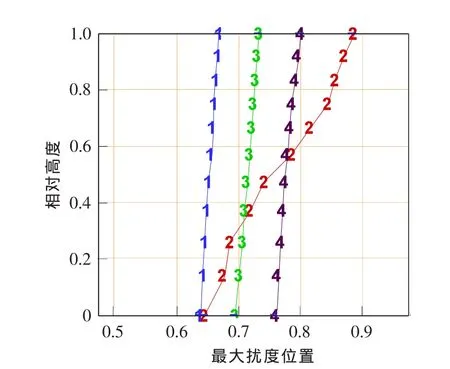
圖1 撓度分布Fig.1 Distribution of deflection

在相對換算轉速1.0下，由ANSYS分析得到的轉子葉片一階振動頻率如表1所示。由表中可以看出，葉片的一階振動頻率隨撓度位置的后移而增大。圖2給出了四種最大撓度相對位置轉子葉片一階振動位移分布，圖中位移量為由ANSYS有限元節點插值轉換到非定常繞流計算網格節點上的結果。從圖中看，四種最大撓度相對位置下的位移量比較接近。上述對應的數據文件將在顫振分析中使用。

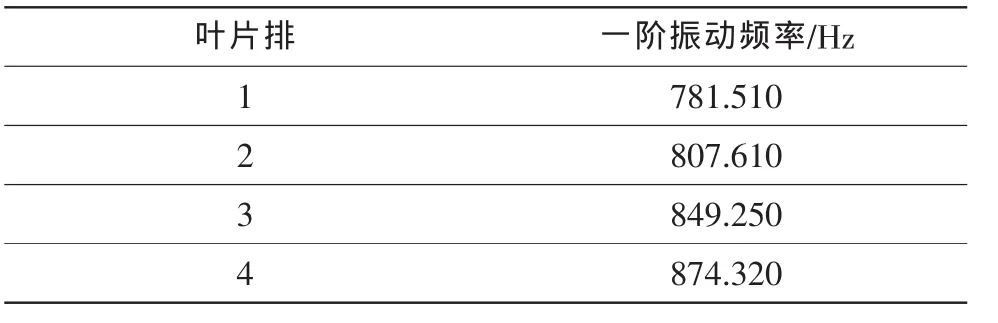
表1 轉子葉片一階振動頻率Table 1 The first order vibration frequency of rotor blade

4 顫振分析

對壓氣機葉片進行結構動力學分析、三維定常分析和顫振分析。根據結構動力學分析得到的葉片自振頻率和位移量分布，進行振動葉片三維非定常繞流計算，可獲得葉片上非定常平均積累總功率，并由此做出氣彈穩定性(顫振)判別[3]。

計算網格：網格數為 31×31×111(周向×徑向×軸向)。葉片網格示意圖如圖3所示。

初場：推進1000時間步，得到收斂的轉子全三維定常流場作為初場。

振動葉片非定常繞流分析：做6個振動周期的非定常計算。

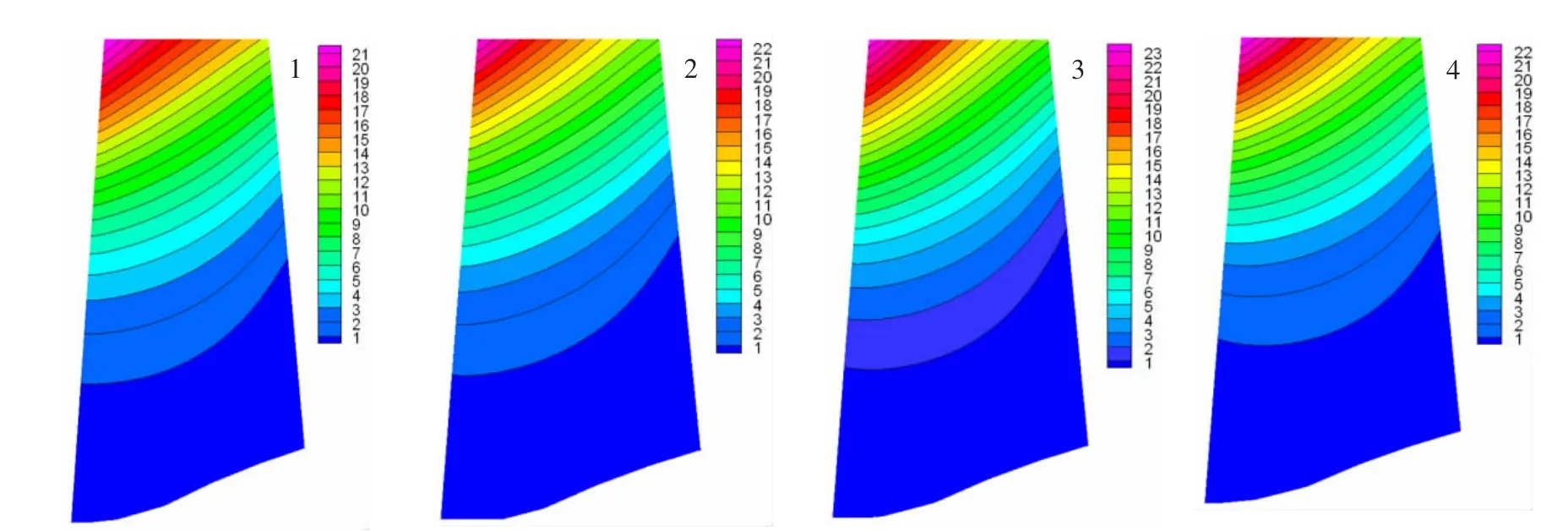
圖2 轉子葉片一階振動位移分布Fig.2 Displacement distribution of compressor rotor blade at first order vibration mode

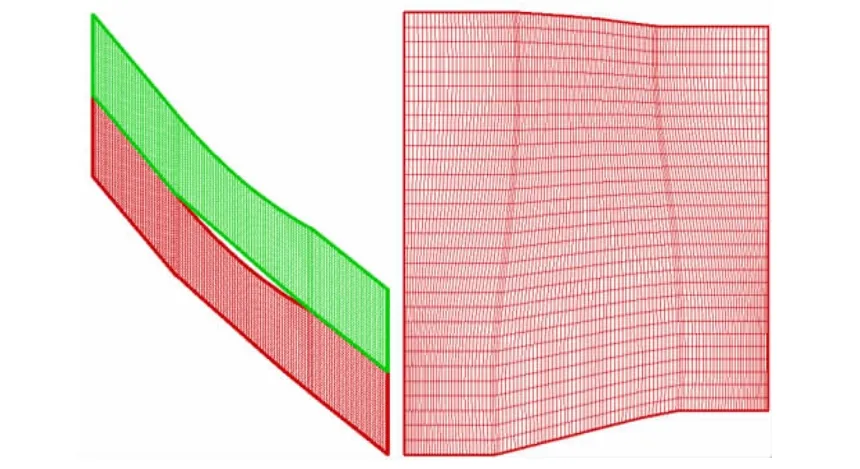
圖3 葉片網格示意圖Fig.3 Computation grid

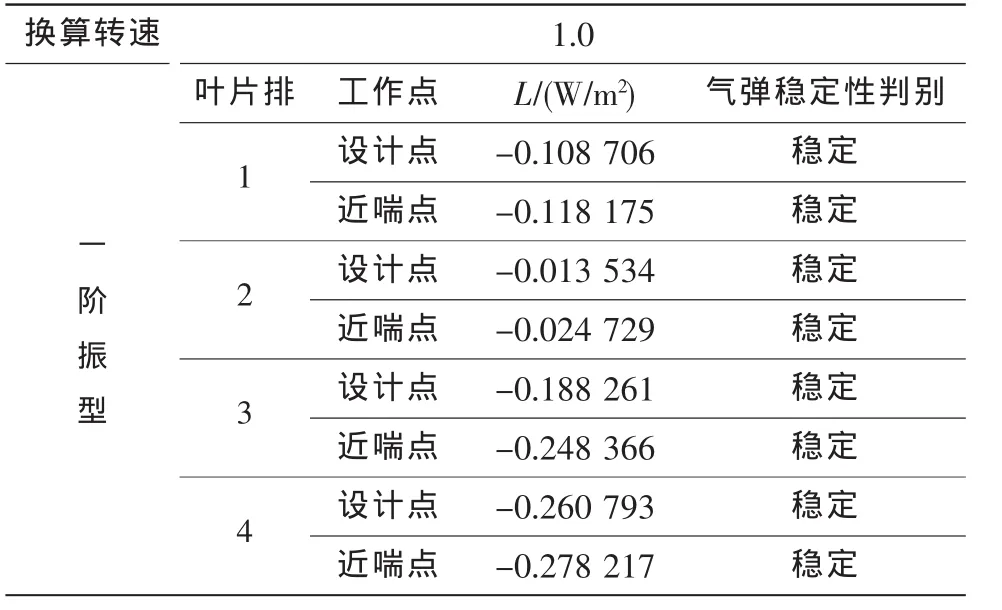
表2 相對換算轉速1.0下的平均積累功率Table 2 Average accumulated power in 1.0 relative corrected speed

根據三維氣動計算結果，計算得到該轉子在設計點和近喘點的壓比，再以此計算葉片的非定常平均積累總功率。表2列出了相對換算轉速1.0下沿特性線計算得到的最后一個周期內葉片的非定常平均積累總功率。由表中可以看出，對于一階振型的顫振，一階臨界點的非定常平均積累功率都為負值，由此判定顫振邊界在三維計算的喘振邊界以外。在撓度分布比較均勻的葉片排1、3、4中，平均積累功率隨撓度位置的后移而減小。由圖4、圖5可以看出，從葉中到葉尖部分，氣流與葉片能量交換比較劇烈；在葉片前緣附近，氣流做負功；在靠近尾緣處，氣流做正功。在葉根部分，氣流基本不做功，氣流與葉片能量交換較小。通過比較可以發現，四種情況下，氣流做正功的區域大致相當，做負功的區域略有差異。在正功區，氣流對葉片排2做功值相對較大；而在負功區，葉片排2葉中區域無明顯負功區。其他三種情況比較接近，葉片排3和葉片排4的葉中負功區最明顯。因此，在相同壓比下，葉片排2葉表的平均積累功率比其他三種葉片排的大，其氣彈穩定性比原始葉片差，更容易發生氣彈失穩。

5 結論

(1)在壓氣機氣動設計中，最大撓度相對位置會影響動葉的一階振動頻率，但對于風扇/壓氣機葉片，一階振動位移分布影響較小。

(2)最大撓度相對位置分布不均勻會大大提高顫振發生的幾率，最大撓度相對位置越大，發生顫振的可能性越小。以上結果為壓氣機葉片設計提供了有益的參考。

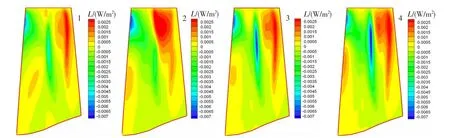
圖4 近設計點平均積累功率分布Fig.4 Average accumulated power distribution at near design points

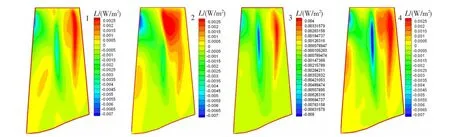
圖5 近喘點平均積累功率分布Fig.5 Average accumulated power distribution at near stall points

[1]張揚軍，陶德平，周 盛.某型風扇葉片顫振研究[J].燃氣渦輪試驗與研究，1996，9(2)：5—8.

[2]施永強，楊青真，周新海.風扇/壓氣機葉型厚度對顫振特性的影響[J].航空學報，2009，30(6)：979—984.

[3]施永強.三維葉片顫振與葉片設計關聯性研究[D].陜西西安：西北工業大學，2006.