基于BP人工神經網絡的基坑圍護結構變形預測方法研究

曾 暉，胡 俊，鮑俊安

(1.五邑大學 土木建筑學院，廣東 江門 529020;2.南京林業大學 土木工程學院，南京 210037)

深基坑工程不僅要保證基坑本身的安全和穩定，而且還要控制基坑周圍地層移動和保護周圍環境。特別是城市軟土地區，由于地層軟弱復雜，進行基坑開挖會產生比較大的變形，嚴重影響周圍建筑物的正常使用和結構安全。在城市基坑工程的設計中，基坑變形控制的要求越來越嚴格，以前以強度控制設計為主的方式逐漸被以變形控制設計為主的方式所取代，因此，基坑的變形分析成為基坑工程設計中的一個重要的組成部分。目前，國內外有多種預測深基坑穩定性的計算理論，但對基坑圍護結構變形的預測方法還不多。基坑變形預測的主要方法包括有限單元法、地層損失法、估算法，以及人工神經網絡預測法［1］。

人工神經網絡(Artificial Neural Network，簡稱ANN)是在研究生物神經系統的啟示下發展起來的一種信息處理方法。該法可以通過大量樣本的學習來抽取出隱含在樣本中的因果關系，具有自適應性、非線性和容錯性強等特點，特別適合于處理各種非線性問題，并且，在大多數情況下，應用效果大大優于傳統的數據處理方法［2］。因此，在巖土工程領域得到廣泛的應用［3］，也為解決基坑圍護結構變形預測問題提供了新的途徑。

1 工程概況

南京地鐵二號線逸仙橋車站建設場地屬古秦淮河漫灘地貌單元，地貌形態單一。車站范圍內地層主要有:雜填土、淤泥質填土、素填土、粉質黏土、粉土、淤泥質粉質黏土、粉質黏土、卵礫石混砂粉質黏土，下臥有強風化泥質粉砂巖、中風化泥質粉砂巖，以及中風化泥巖。地下水類型為孔隙潛水和孔隙微承壓水。孔隙潛水水位穩定埋深1.35～1.80 m，設計地下水埋深1.00 m。孔隙微承壓水水位與孔隙潛水水位一致。

車站總長161.6 m，標準段寬21 m，車站地底板埋深約22 m。基坑主體部分由三部分組成:西端頭井約為23.32 m×23.40 m的矩形基坑，開挖深度為24 m;標準段(分為七段)約為123.88 m×21.00 m的矩形基坑，開挖深度為22 m;東端頭井約為14.4 m×23.7 m的矩形基坑，開挖深度為23 m。圍護結構采用800 mm地下連續墻，嵌入深度約19.5 m。采用內支撐支護結構方式，選用直徑為 φ609 mm鋼管支撐，支撐壁厚t=12 mm(第一道支撐)和t=6 mm(其它幾道支撐)。第一道支撐水平間距6 m，其余支撐水平間距為3 m左右。基坑豎向設置六道鋼支撐加一道倒換支撐保持穩定。車站施工采用明挖順筑法施工［4-5］。

對本工程的監測從2007年1月28日開始，工程在開始監測的同時開始施工。深基坑開挖引起地下連續墻兩側的壓力差將會導致墻體發生變形［1］。現場在西端頭井、標準段和東端頭井均進行了圍護結構墻體變形測試，安裝了CX01～CX16測點共計16個監測點。CX15測點位于西端頭井北側，其在各施工階段水平位移如圖1所示。

圖1 CX15測點墻體在各施工階段的水平位移

2 建立ANN模型

2.1 BP神經網絡模型

為了準確建立基坑圍護結構變形預測模型，采用目前土木工程中應用最廣泛的BP神經網絡。它是一種前饋式多層神經網絡模型，誤差反向傳播。模型由輸入層、輸出層及隱層組成，每一個節點層都包括一定數量的神經元節點，同一節點層各節點之間互不連接，如圖2所示。

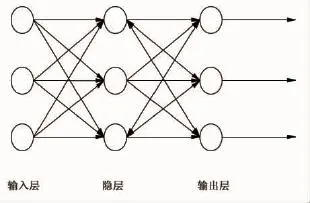
圖2 最基本BP網絡結構

2.2 影響基坑圍護結構變形的因素

影響圍護結構變形的主要因素包括:基坑的工程地質與水文地質條件;支護類型及結構設計參數;基坑平面尺寸及開挖深度;施工過程和場地周邊環境;施工工期的影響;地面超載和震動荷載;支撐條件;圍護結構的剛度;圍護結構在坑底以下的入土深度;土層強度(包括土體的黏聚力c、內摩擦角φ值等);地下水的影響等。

2.3 網絡結構的確定

基坑圍護結構的變形是各影響因素綜合作用的結果。結合實際情況，從各因素中選取施工工期(T)、開挖深度(D)、地下水位高度(W)、當天氣溫(C)共4個具有代表性的指標作為網絡的輸入。選用CX15測點某一高度處的變形量S為網絡的輸出。取一個隱含層，節點數取10個(為輸入層神經元數 n的(2n+2)個，見圖3)。在影響圍護結構變形的各個因素中，基坑的工程地質與水文地質條件、支護類型及結構設計參數、地面超載和震動荷載、土層強度(包括土體的c、φ值等)對各樣本變形觀測值的影響是均等的，故在影響因素的選取時不考慮其對變形結果的影響［6］。

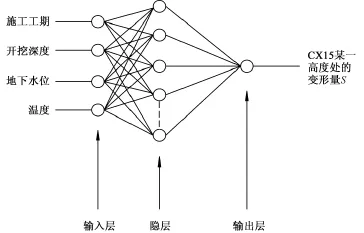
圖3 確定CX15某一高度處的變形量S的神經元模型

為確定CX15測點17.5 m高度處的變形量(S)是否與施工工期(T)、開挖深度(D)、地下水位高度(W)、當天氣溫(C)存在客觀的相關性，分別對它們進行了相關性分析，如圖4所示。相關系數 R2越大，說明兩組統計數據之間的相關性越大。可以看出，當天氣溫(C)對CX15測點17.5 m高度處的變形量(S)的影響較大，而施工工期(T)、開挖深度(D)、地下水位高度(W)對其影響很明顯。

2.4 網絡訓練和檢驗

以收集到的15個不同工況下CX15測點的墻體變形監測值為神經網絡的學習訓練樣本，采用Visual C++來開發的NNBP1.0程序進行學習和檢驗。當網絡迭代運算至10 000次或者目標函數 εAV小于預先給定的ε=1.0×10-6時，跳出循環，訓練結束。

從學習訓練樣本的實際輸出與希望輸出對比可知，最大誤差為0.93%，平均誤差為0.17%。從表1可看出，各值十分逼近，表明模型的擬合精度是較高的。BP網絡實現了從輸入的p維歐氏空間到輸出的q維歐氏空間的降維映射，因此，可用于非線性分類、預測等領域，并且作為一個函數計算器，能以任意精度逼近任何非線性函數。

圖4 施工工期、開挖深度、地下水位高度和當天氣溫與CX15測點17.5 m處變形量的關系

表1 學習訓練樣本的實際輸出與希望輸出對比

3 圍護結構變形預測分析

首先，從最簡單的預測開始，分析預測CX15測點17.5 m深處的水平位移。選取15組數據中的前12組數據為學習訓練樣本，后3組數據作為測試樣本。學習訓練樣本數據見表2。

使用 Visual C++來開發的 NNBP1.0程序，需將訓練樣本作歸一化處理。將需訓練的前12組數據輸入NNBP1.0程序后，便可進行訓練。學習訓練完畢后，就形成了一個對應于該學習訓練樣本的神經網絡。接著，讓訓練好的神經網絡來預測后3組數據，預測的圍護結構水平位移歸一化結果為0.788 279 884，0.863 980 662，0.968 068 530，再反歸一化得到最后結果:3月21日為20.4 mm;3月25日為22.0 mm;3月28日為24.2 mm。而實測值是:3月21日為20.4 mm;3月25日為22.3 mm;3月28日為24.9 mm。可見，預測值與實際值非常接近。

表2 學習訓練樣本數據

在預測分析上面數據的同時，分別以前10組、11組、12組、13組、14組為學習訓練樣本，對它們之后的數據進行預測，結果見表3。

表3 預測值取前 10、11、12、13、14組數據為訓練樣本的預測結果對比

由表3可知，利用上述建立的神經網絡方法對基坑圍護結構變形作短期預報是完全可行的，且十分有效。但相對而言，較長期的預報值誤差較大。同時也說明，雖然神經網絡方法能有效地進行變形預報，但現場監測工作仍需繼續進行。

以上工作完成了對CX15測點17.5 m深度處的變形量的預測，用同樣的方法，可以預測CX15測點不同深度處的變形量。以相同的方法訓練神經網絡，分別對3月21日和3月25日基坑圍護結構總的變形進行了預測，并同時與實測值進行對比，如圖5所示。結果表明，預測值與實測值都非常接近，曲線吻合很好，訓練所得的網絡具有較強的預測能力，可用于基坑圍護結構變形的短期預測。

圖5 變形實測值與預測值對比

4 結語

1)利用大量的基坑工程現場實測資料，采用神經網絡BP算法，可以較為準確地預測基坑圍護結構的變形量，預測值與實測值吻合較好。如果資料更全面，則預測會更準確。

2)影響基坑圍護結構變形的因素具有復雜性和多變性，采用人工神經網絡，以根據需要充分考慮各因素的影響，提高預測的準確度。本實例運用的樣本數偏少，主要目的是提出一種思路。

3)從學習訓練樣本的實際輸出與希望輸出對比可知，最大誤差為0.93%，平均誤差為0.17%。BP網絡實現了從輸入的p維歐氏空間到輸出的q維歐氏空間的降維映射，因此，可用于非線性分類、預測等領域，并且，作為一個函數計算器，能以任意精度逼近任何非線性函數。

4)現場實時監測仍是必要的，由表3可以看出，短期預報精度較高，但較長期的精度不高。同時，影響基坑圍護結構位移變化趨勢的某些因素，在施工前期沒有發揮作用。但隨著施工和監測的進行，新的變化數據不斷得到收集，這些數據又進一步反映了基坑圍護結構變形的趨勢。因此，必須堅持現場監測，并將最新監測信息及時反饋，將其添加到學習訓練樣本中，讓神經網絡重新學習，以提高基坑工程圍護結構變形的預報精度。

［1］劉建航，侯學淵，劉國彬，等.基坑工程手冊(第二版)［M］.北京:中國建筑工業出版社，2009.

［2］胡伍生.神經網絡理論及其工程應用［M］.北京:測繪出版社，2006.

［3］高浪，謝康和.人工神經網絡在巖土工程中的應用［J］.土木工程學報，2002，35(4):77-81.

［4］胡俊，潘悅，光輝.南京地鐵某車站深基坑開挖的監測與分析［J］.西部探礦工程，2008，20(10):222-225.

［5］胡俊，陳爭.南京某車站深基坑開挖圍護結構的變形分析［J］.山西建筑，2007，33(21):98-99.

［6］胡俊，楊平，董朝文，等.盾構始發端頭化學加固范圍及加固工藝研究［J］.鐵道建筑，2010(2):47-51.