基于廣域信號的區域間低頻振蕩監視

常勇，吳靖，王超

（1.國家電網公司 運行分公司,北京 100053，2.杭州市電力局，浙江 杭州 310009；3.浙江省電力公司，浙江 杭州 310027）

當聯絡線傳輸功率過重時，同步發電機阻尼轉矩不足而導致的低頻振蕩是限制跨區交換容量的瓶頸之一，它嚴重威脅到電力系統的安全穩定運行[1-3]。1996年北美大停電的初始階段，主要潮流斷面上均觀察到明顯的低頻振蕩現象，并最終導致大范圍的電網解裂，而整個事故發展時間跨度有幾十分鐘。2003年美加大停電事后,對事故發展過程的調查表明,這次大停電事故也是由區域性故障逐步發展而來[4]。可以想見，如果在系統振蕩發生的初始階段及時判斷發現動態不穩定現象，并經分析給出合理的控制策略，就能及時緩解故障對系統的沖擊，避免故障大范圍擴散。

傳統上研究大型系統低頻振蕩問題常采用特征值分析的方法，如QR算法等。但是當前實際電力系統規模較大、維數較高、實際計算有較大困難,而在線辨識的方法則可以避免維數災問題[5]。廣域測量系統(Wide Area Measurement System,WAMS)給電力系統的實時動態監測控制手段帶來了新的發展契機[6-8]。WAMS系統可以直接量測電力系統電壓電流等相量，并且利用GPS同步授時，各數據量被加上同步絕對時間時標，數據間的理論時間誤差只是GPS系統誤差。測量數據較之SCADA測量數據精度及時間準確性大大提高，借助高速的通訊手段，這些數據可以用作全網動態實時監測的寶貴數據源[9]。

本文首先提出了實時同步監測和實時控制的雙層低頻振蕩監控中心體系結構，然后比較了已有報道的若干種低頻振蕩實時監測算法，最后針對若干測試系統及一個實際系統小擾動后的時域響應曲線詳細比較了Prony方法和ESPRIT方法辨識低頻振蕩的技術特性，獲得了一些指導其在線應用的結論。

1 電力系統低頻振蕩監控系統結構

在全網同步相量監測的基礎上，在線電壓穩定控制、在線頻率穩定控制、實時網架拓撲連通性分析、以及實時事件記錄等高級功能都可以實現。構想中的全網實時低頻振蕩監控中心在概念上應該屬于全網動態監控系統（AEMS）中的一個功能模塊，在物理實現上,可以與其余高級功能共用PMU、數據集中器、網關、工作站等設備[10]。

特征值分析方法和模態辨識方法各有其優缺點：特征值分析可以獲得詳盡的系統信息，然而其耗時多，準確性取決于對電力系統模擬的精度。模態辨識的方法具有實時性好的優點，但是其分析結果受信號噪聲影響較大。低頻振蕩監控中心的信號流程如圖1所示。

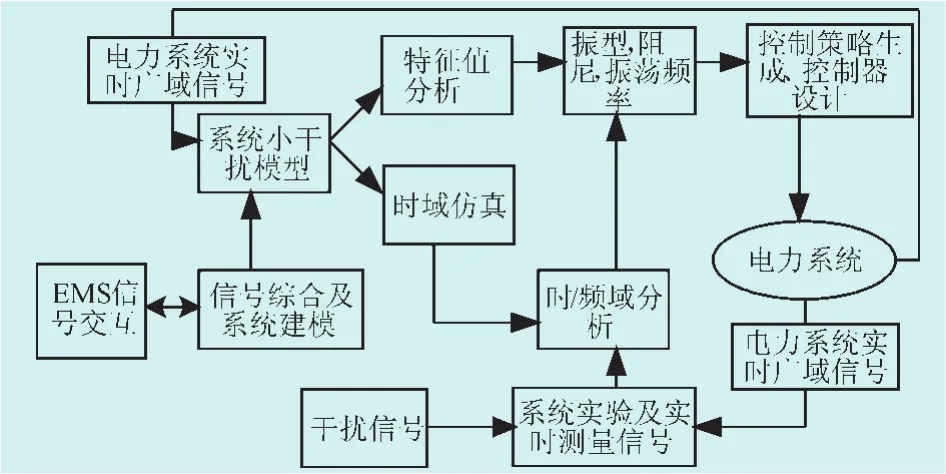
圖1 低頻振蕩監控系統信號流程圖

實時的電力系統運行工況信號與EMS系統信號相結合，在線更新電力系統小擾動模型。在此基礎上可以進行準實時的特征值分析以及時域仿真分析。特征值分析可以方便地得到整個系統的振型、阻尼、振蕩頻率等關鍵量，可以決定反饋信號、設計控制器結構以及控制施加地點。時域仿真結果同樣可用于時/頻域分析，其結果可以和實時反饋信號的時/頻域分析結果相互校核。電力系統實時信號經過頻域或時域分析后，結合在線準實時特征值分析的結果調整閉環控制器參數，然后系統將控制信號反饋回電力系統實現實時控制。直接對反饋信號進行時/頻域分析速度較快，其結果可以作為在線監視以及在線調整控制器參數的主要依據。

2 電力系統低頻振蕩在線辨識方法

實現低頻振蕩實時監控的基礎是振蕩模式等特征量的實時在線辨識，模態辨識方法層出不窮，但是從辨識方法上歸納，主要可以分為基于模型參數的辨識方法和非參數化辨識方法。前者主要包括基于模型參數的AR方法[11-12]、Prony方法[13]。另外，近年來發展起來的子空間方法 (Subspace)也有其可取的優點[14]，從本質上說,也屬于基于模型參數的模態辨識方法。非參數化的方法以傅里葉變換算法為主，在其基礎之上發展了滑動窗傅里葉變換(Sliding Window Fourier Transformer)等算法提高了算法的工程適用性[15]。

2.1 ESPRIT方法

ESPRIT方法(Estimation of Signal Parameters via Rotational Invariance Techniques，ESPRIT)即基于總體最小二乘法——旋轉不變技術的信號參數估計方法，是一種基于子空間的高分辨率的模式辨識算法，最初該算法多用于雷達信號處理[16]，在文獻[17]中將其應用到電力系統低頻振蕩特性辨識上。類似Prony算法，此方法可利用電力系統測量數據或者時域仿真數據分析電力系統的低頻振蕩問題，不受電網規模的限制，克服了傳統特征值分析法的局限性。但ESPRIT是一種基于子空間的辨識方法，直接以數據序列構成的Hankel數據矩陣為基礎，把信號空間分解為信號子空間和噪聲子空間，理論上可以高精度地辨識電力系統中任意組合的衰減/非衰減正弦信號的頻率、相位和幅值等參數信息，具有較強的抗噪聲能力。它避免了求取信號的自相關矩陣(correlation matrix)，簡化了計算。另外ESPRIT方法采用奇異值分解(Singular value decomposition，SVD)等計算方法，數值計算穩定性和魯棒性更好,能夠在較短的信號長度內準確辨識出系統低頻振蕩的主導模式（dominant mode）。TLS-ESPRIT是ESPRIT的改進算法，作為諧波恢復，振蕩衰減正弦信號參數估計的有效工具，目前已被廣泛地應用于雷達陣列信號，語音信號，生物信號處理等場合[18]。TLS-ESPRIT算法近年來也被引入到電力系統中，應用于諧波和間諧波高精度檢測，暫態信號分解[19]等場合。該算法的原理框圖如圖2所示。

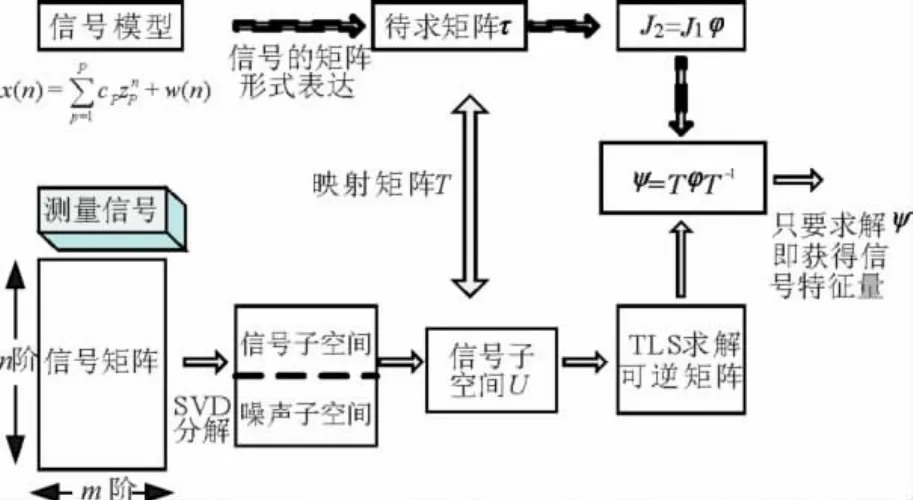
圖2 ESPRIT算法的原理框圖

2.2 Prony方法

Prony方法是用指數函數的線性組合來擬合等間隔采樣數據的方法，可以從中分析出信號的頻率、衰減因子、幅值和相位。和特征值分析方法相比，Prony方法是模態參數辨識的時域方法，不用求解大規模系統的特征值，其系統模型的階數可以根據辨識的目的和需要等確定。Prony方法對實時測量的系統數據進行分析，最大的問題是如何避免噪聲信號的影響[20-21]。

2.3 FFT方法

傅里葉變換算法是譜分析非參數化方法中常用的一種，它的優點很多，例如：對信號噪聲不敏感；可利用FFT快速傅里葉算法，計算速度快，有利于在線使用；另外不易出現模型失配的情況。考慮到算法的柵欄效應，為了避免頻譜泄漏，文獻[22]利用滑動窗FFT算法提高了在線模態辨識的精度。

2.4 子空間方法

近年來子空間方法被廣泛地應用于隨機信號模型辨識，文獻[14]給出了子空間模型辨識方法的主要原理及步驟。與傳統方法相比，子空間方法具有數值穩定性好（采用QR算法、最小二乘法、以及奇異值分解等算法）、無須優化過程計算速度快、可以方便地進行多輸入多輸出(MIMO)系統辨識等優點。子空間方法的核心思想是首先基于輸入輸出數據構建系統狀態相量，然后在此基礎上求解最小二乘問題，得到系統的傳遞函數矩陣，最后求解此傳遞函數矩陣即可以獲得表征系統動態特性的各量。子空間辨識基本算法主要有3種，即：MOESP(multivariable output error state space)、N4SID(numerical algorithm for subspace state space system identification)以及CVA(canonical variable analysis)。

3 在線辨識算法綜合分析

3.1 在線辨識算法的普適要求

實際應用于電力系統辨識的算法則需要滿足以下幾個性能要求。

1）準確性。實際電力系統采樣信號往往被噪聲污染，通過上一節的分析，考慮到計算效率以及在線實現的方便性，Prony方法和ESPRIT方法更加適合于低頻振蕩的在線實時分析。筆者將以若干參考系統和一個實際系統為例，檢驗比較這兩種算法的計算精度和實際效率。

從工程實際出發，不同辨識算法的比較主要從辨識精度和算法耗時兩個角度評價。衡量分析結果有兩個指標：信噪比和百分比誤差。假設真實數據為x（k），算法模型輸出為x（k）,k=0,1,…,N-1。

一是信噪比(Signal/Noise Ratio,SNR)，它是最常用的指標，其定義為

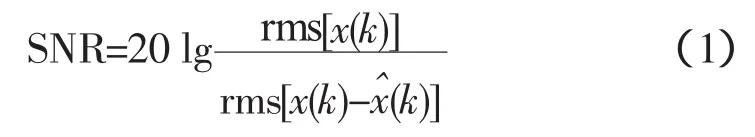
式中，rms表示均方根(root mean square)，單位為dB。有些程序中的SNR表達式略有不同。

二是百分比誤差Dp，其定義為

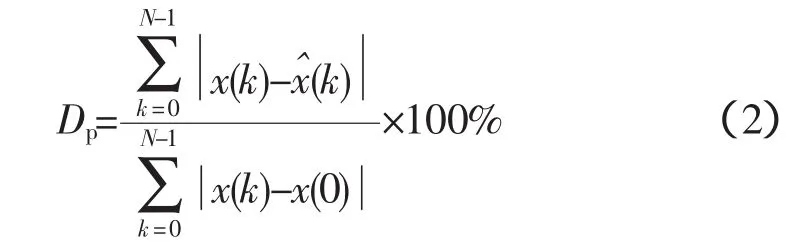
一般認為，百分比誤差小于10%以及SNR達到20dB以上時，算法分析得到可以接受的結果，接近40 dB，則更加理想。另外，通過比較真實數據曲線和擬合數據曲線，也可以作為一種輔助手段直觀地判斷擬合的效果。

當各模態參數都已獲得時，即可以重構所辨識信號，與真實采樣值進行比較。在同一幅圖形中分別描繪出它們的波形，以查看擬合的效果。

2）抗噪聲。實際電力系統信號在采樣和傳輸過程中不可避免地受到噪聲干擾，故障后系統的響應中更是會有許多雜散的頻率分量。因此算法對噪聲的敏感性應該比較低，算法本身最好具有一定的濾波效果。

3）快速性。為了達到在線實時或者準實時辨識的目的，對算法的耗時有較高的要求。實際工程中，采用哪種算法，很大程度上受算法時間性限制。

4）分辨率。辨識算法多種多樣，辨識結果往往是一系列的頻率分量。實際采用的算法應能夠在這一系列頻率分量中準確地找到所關心的系統主導振蕩模式。

5）穩定性。辨識算法應具有算法穩定性，實際應用中是循環辨識過程，算法可能需要復用歷史數據，這時要求算法在做長時間計算過程中不會受到誤差積累等因素的影響。

3.2 辨識模型定階

模型階數P的確定是辨識算法的重要問題，但實際大型互聯電力系統動態過程中，系統階數是未知的，并且是高維的，用于擬合的模型都只能是一個降階的近似模型。但是需要指出的是，通常我們最關心的是系統低頻振蕩的主導模式，并不要求獲得所有的振蕩模式。

本文提出一種辨識自適應定階方法，首先取定一個初始定階分辨率，然后進行信號辨識，最后通過判斷Dp、SNR等指標是否滿足預設要求，滿足則輸出結果，否則調整定階分辨率，繼續求解，整個計算流程如圖3所示。

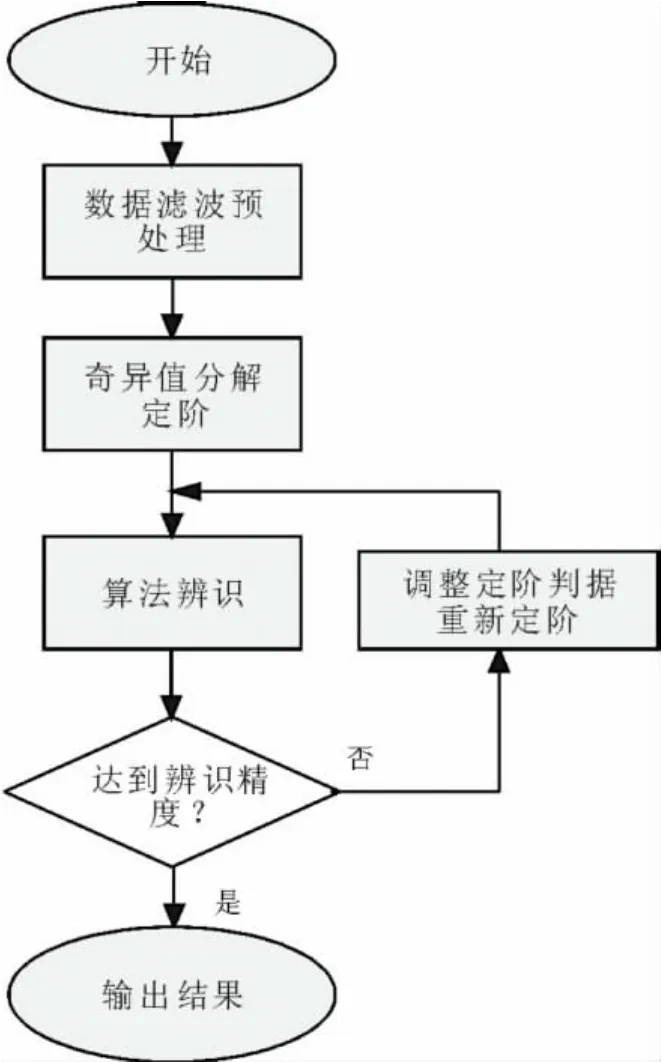
圖3 自適應定階算法的原理框圖

4 算例分析

文獻[5]中的四機兩區域系統是一個典型的包含區域間振蕩模式和區域內振蕩模式的測試系統。其潮流分布見圖4。

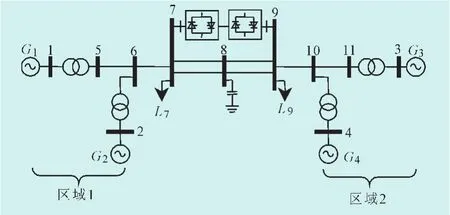
圖4 四機兩區域交直流系統

首先利用PSS/E自帶的小信號分析工具LSYSAN，對該系統進行小擾動分析，結果見表1。

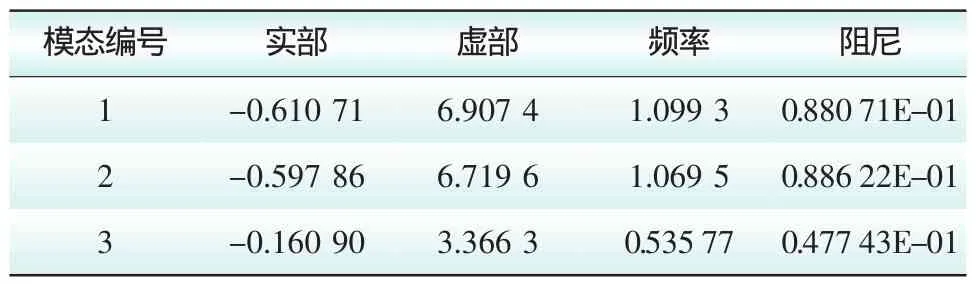
表1 四機兩區域系統的特征值分析結果

由分析結果可見，該系統存在3個振蕩模式，其中1、2兩個模式振蕩頻率在1 Hz左右，是區域內振蕩模式，模式3振蕩頻率是0.536 Hz，為典型的區域間振蕩模式。同時，3個振蕩模式的阻尼都小于10%，系統阻尼不足。

其次，利用PSS/E的時域仿真功能獲取系統小擾動下的動態響應曲線。需要特別注意施加的擾動必須足夠小，其標準是系統仍然在初始平衡點附近工作。否則在大擾動下系統已經偏離初始穩定運行點，那么以線性化的方法套用到非線性系統，勢必得不到準確的結果。因此在這里采用微調系統負荷的方法獲得系統的線性化響應，具體為調整母線7上的負荷5 MW[23-25],仿真結果見圖5。

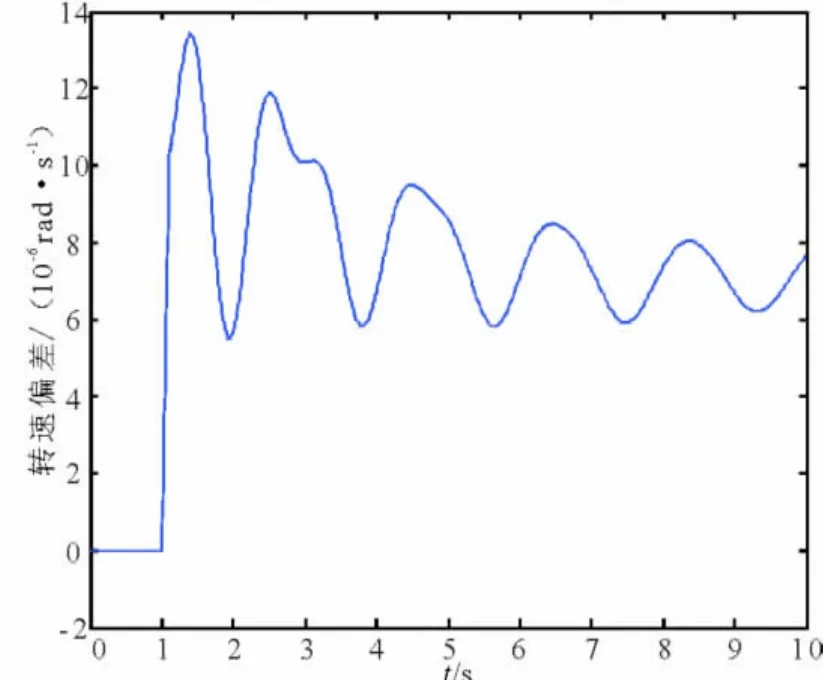
圖5 發電機1的轉速偏差

觀察圖5后，截取擾動后的振蕩線性化部分，即6.5 ～10 s之間的部分進行辨識，模態辨識的結果以及相關的辨識評價指標如表2所示，重構分析結果見圖6、圖7。注意這里僅列出了區域間振蕩模式的辨識結果（以下的討論中也相同）。

表2 四機兩區域系統的小信號分析結果

接著對7 ～8支路上傳輸的有功功率分別利用兩種方法進行辨識，所得的結果如圖8所示。

模態辨識的結果以及相關的辨識評價指標如表3所示，重構分析結果見圖9、圖10。

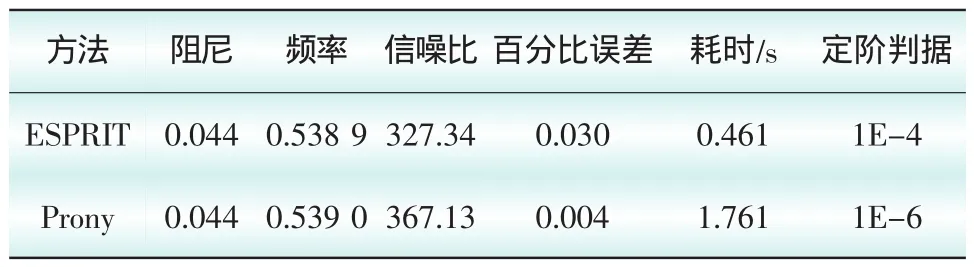
表3 四機兩區域系統的小信號分析結果

接下來取1號和3號發電機之間功角差為辨識對象，其形如圖11所示。

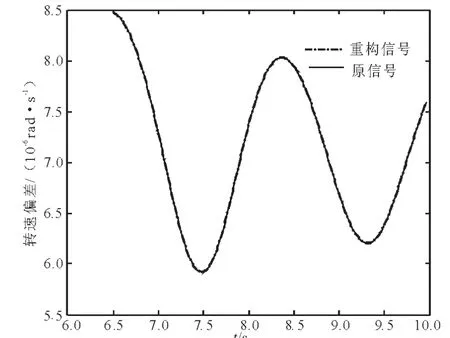
圖6 ESPRIT方法的重構圖形比較

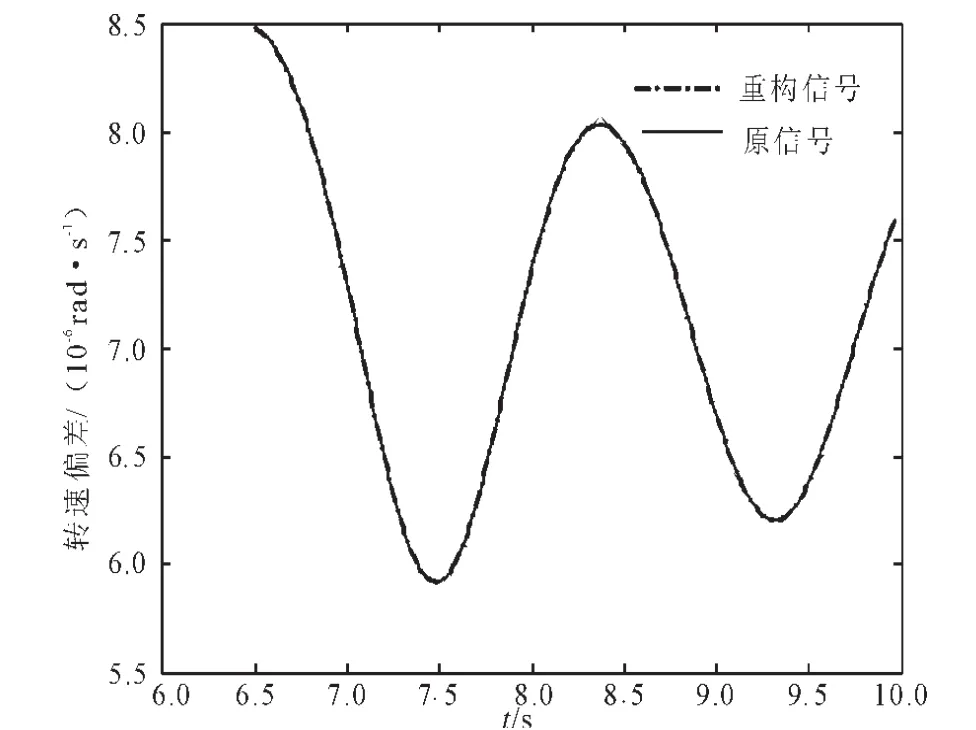
圖7 Prony方法的重構圖形比較

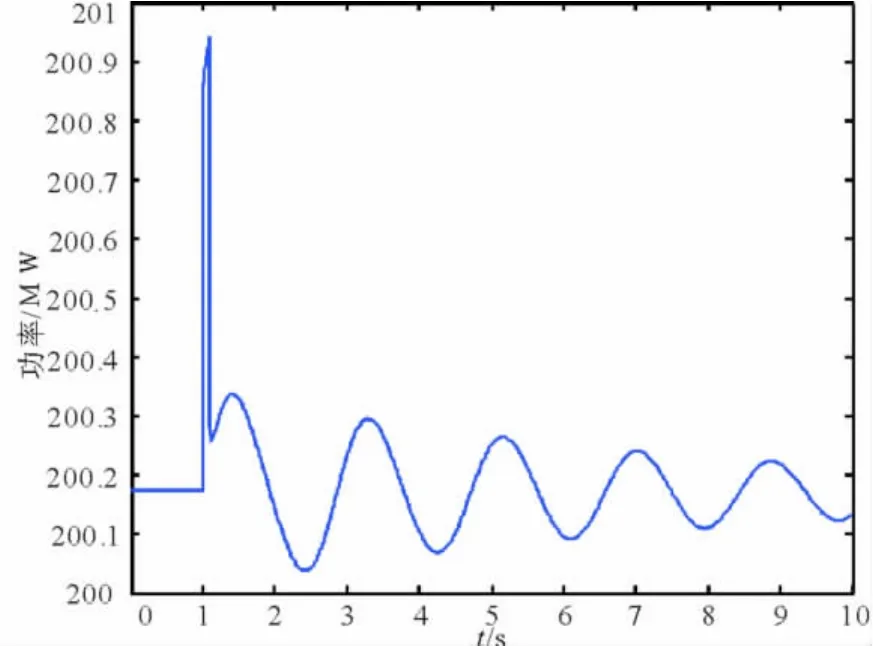
圖8 7 ～8支路功率

模態辨識的結果以及相關的辨識評價指標如表4所示，重構和結果見圖12、圖13。

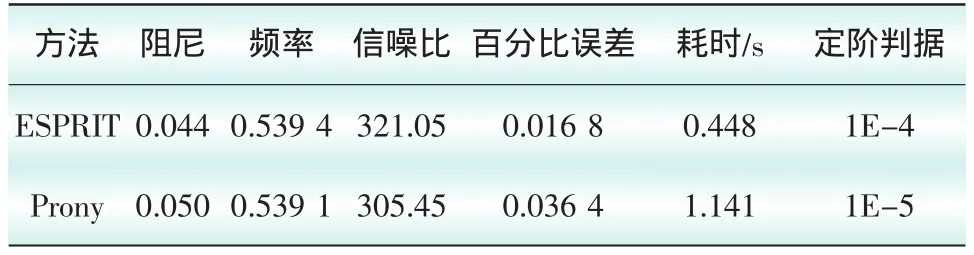
表4 四機兩區域系統的小信號分析結果

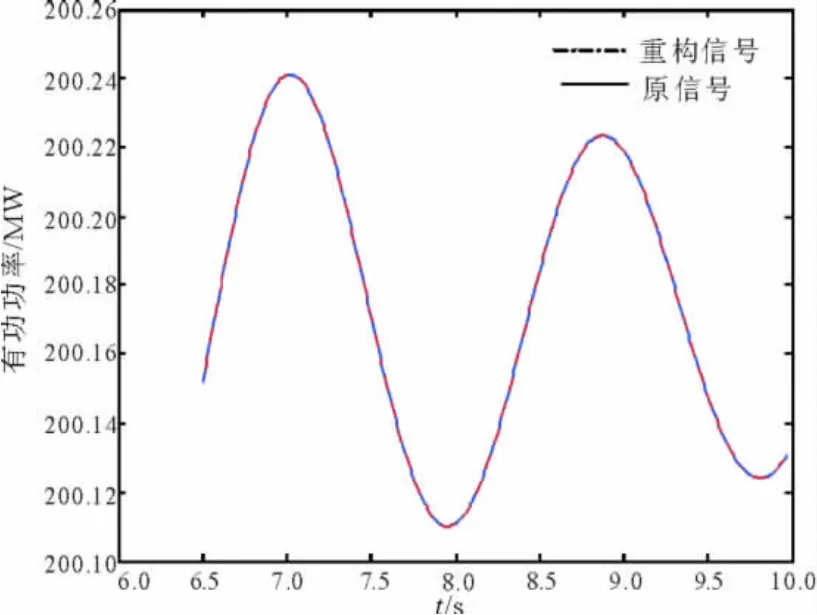
圖9 ESPRIT方法的重構圖形比較

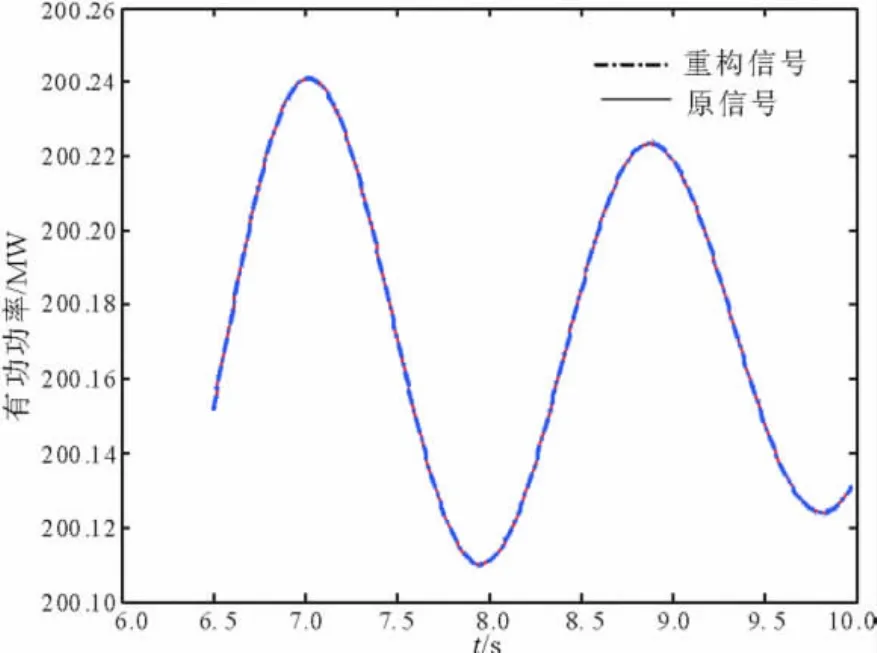
圖10 Prony方法的重構圖形比較

圖11 發電機1，3的功角差

圖12 ESPRIT方法的重構圖形比較

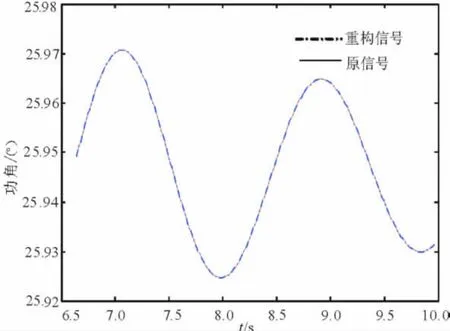
圖13 Prony方法的重構圖形比較

經上述算例驗證，可見Prony方法和ESPRIT方法均能很好地實現辨識，在選擇適當的定階判據后，百分比誤差均小于5%。同時兩種方法進行在線辨識的耗時均不超過2 s，這對于在線發現和判定動態失穩有重要的意義，有利于后續補救控制的實施。

5 結論

本文圍繞電力系統低頻振蕩監控系統的組成結構展開研究。第一個核心內容是提出了從監測到控制的雙層體系結構。其次針對監測時需要用到的模式辨識方法做了研討，分析比較了不同辨識方法的優劣，重點比較了Prony和ESPRIT兩種方法。從在線辨識算法的工程要求出發討論了辨識窗長度、噪聲影響等關鍵問題，在分析重構定階標準對重構精度的基礎上提出一種適用于Prony以及ESPRIT方法的電力系統低頻振蕩實時監測定階算法。得出的主要結論如下：

1）在線辨識算法應用時，取不同長度的數據段計算復雜度顯然不同，耗時也有明顯的區別。過長的辨識窗可能引入更多的噪聲，給辨識算法定階帶來困難。

2）通過對不同信號的算例檢驗發現，相對功角信號作為辨識對象往往可以大大縮減定階數，定性地看，功角信號和轉速信號更直接地反映了發電機的動態過程，信號本身受噪聲影響較小。

[1] 劉振亞.加快建設堅強國家電網促進中國能源可持續發展[J].中國電力，2006,39(9):1-3.

[2] 李丹,蘇為民,張晶,等.“9.1”內蒙古西部電網振蕩的仿真研究[J].電網技術,2006,30(6):41-47.

[3] 余貽鑫,李鵬.大區電網弱互聯對互聯系統阻尼和動態穩定性的影響[J].中國電機工程學報，2005，25(1):6-11.

[4] 蔡洋.電網調度管理須與電網發展俱進—北美東北電網事故淺析[J].電網技術,2004,28(8):6-10.

[5] K UND UR P.Power System Stability and Control[M].New York:McGraw-Hill Inc,1994.

[6] 王克英,穆鋼,陳學允.計及PMU的狀態估計精度分析及配置研究[J].中國電機工程學報,2001,21(8):29-33.

[7] 李丹,韓福坤,肖晉宇,等.華北電網廣域實時監測系統[J].電網技術，2004，28(23):52-56.

[8] 胡志祥,謝小榮,肖晉宇,等.廣域測量系統的延遲分析及測試[J].電力系統自動化,2004,28(15):39-43.

[9] GRIGSBY L L.The Electric Power Engineering Handbook[M].Cleveland:CRC Press,2000.

[10] 盧強.南方電網的災變防治體系——南方電網的Super EMS[J].電力系統自動化,2005,29(24):1-2.

[11] KORBA P,LARSSON M,REHTANZ C.Detection of Oscillations in Power Systems Using Kalman Filtering Techniques[C].IEEE Conference on Control Applications,2003.CCA 2003.Turkey:Istanbul,CCA 2003（1）：183-188.

[12] ZHANG Xiaoping,CHRISTIAN Rehtanz,BIKASH Pal.Flexible ACTransmission SystemsModelingand Control[M].New York:Springer,2006.

[13] HAUER J F，DEMEURE C J,Scharf L L.Initial result in Prony Analysis of Power System Response Signals[J].IEEE Transactions on power system,1990,5(1):80-89.

[14] OVERSCHEE P,MOOR B D.Subspace Identification for Linear Systems:Theory,Implementation,Applicalions[M].Boston:Kluwer AcademicPublishers,1996.

[15] TAKASHIHiyama,NAOTOSuzuki,TAKAHIKOFunakoshi.Online Identification of Power System Oscillation Modes by Using Real Time FFT[J].IEEE Power Engineering Society Winter Meeting,2000,2(1):1521-1526.

[16] 張賢達.現代信號處理[M].北京:清華大學出版社,2000.

[17] 張靜,徐政,王峰,等.TLS-ESPRIT在低頻振蕩分析中的應用[J].電力系統自動化2007,31(20):84-88.

[18] DIMITRIS G,VINAY K INGLE,STEPHEN M,et al.Statistical and Adaptive Signal Processing[M].London,Artech House Press,2005.

[19] BOLLEN M H J,STYVAKTAKIS E,IRENE G,et al.Categorization and Analysis of Power System Transients.IEEE Transactions on Power Delivery[J].2005,20(3):2298-2306.

[20] 蘆晶晶,郭劍,田芳,等.基于Prony方法的電力系統振蕩模式分析及PSS參數設計[J].電網技術,2004,28(15):31-34.

[21] 劉紅超,李興源.基于Prony辨識的交直流并聯輸電系統直流阻尼控制的研究[J].中國電機工程學報,2002,22(7):54-57.

[22] 鞠平,謝歡,孟遠景,等.基于廣域測量信息在線辨識低頻振蕩[J].中國電機工程學報,2005,25(22):56-60.

[23] 肖晉宇,謝小榮,胡志祥,等.電力系統低頻振蕩在線辨識的改進Prony算法[J].清華大學學報：自然科學版,2004,44(7)：883-887.

[24] 姚李孝,寧卜,沈東方,等.異步運行狀態下振蕩中心研究[J].電網與清潔能源,2008,24(12):16-20.

[25] 李鵬,徐光虎,劉春曉,等.從時頻角度重新審視南方電網的區間功率振蕩[J].南方電網技術,2010,4(1):6-10.