工程計算巧用矢量正交分解法
何念民
(四川川投田灣河開發有限責任公司發電總廠,四川 石棉 625400)
工程計算巧用矢量正交分解法
何念民
(四川川投田灣河開發有限責任公司發電總廠,四川 石棉 625400)
將矢量定義引用到工程計算中進行運用,推論出機組最佳中心法,進而將最佳中心法推廣運用到推力軸承加墊計算、軸心擺度中心軌跡計算等方面。
矢量定義;最佳中心法;推力軸承加調整墊計算;軸心擺度軌跡
0 引言
在數學中矢量的定義是既有大小又有方向的量;在物理學中既要由數值大小(包括有關的單位),又要由方向才能完全確定的量叫物理矢量,這些量之間的運算并不遵循一般的代數法則,而遵循特殊的運算法則,如矢量相加減遵循平行四邊形法則、三角形法則、多邊形法則等。常見矢量分析法就是正交分解法,正交分解就是將一個矢量按平行四邊形法則把矢量分解到互相垂直的兩個方向上,然后再求每個方向上的分矢量和,這樣就把復雜的矢量運算轉化成簡單的代數運算。正交分解法的優越性就是方便求解不在一條直線上的多個共點矢量的和矢量。如圖1,將矢量ri分解成了沿X軸方向的Xi和沿Y軸方向的Yi的兩矢量。Xi、Yi遵循矢量運算法則,公式為:

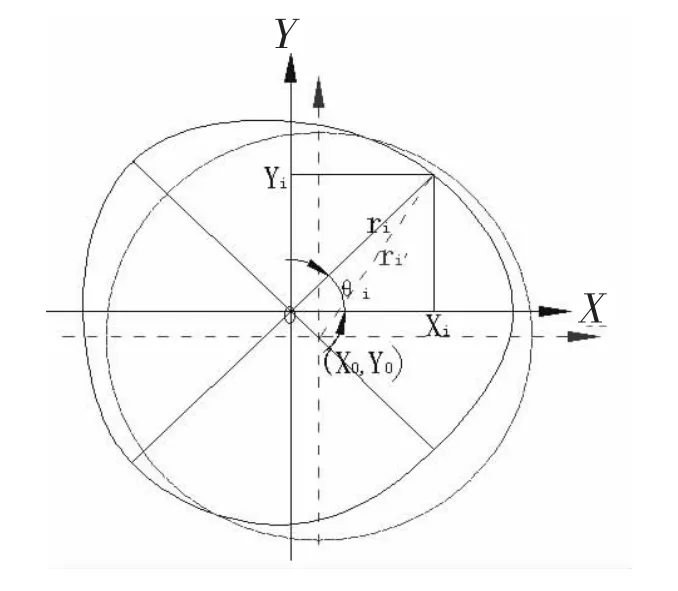
圖1 矢量正交分解圖
1 巧用矢量正交分解推出機組最佳中心法
在水電機組安裝工程中,經常會對機組進行中心測量和調整,常規方法就是在機組軸線位置測量圓周半徑,進行中心調整。為更準確地進行中心調整,需要更多地對機組中心數據進行測量和分析,利用常規方法進行計算就難以處理和分析多組數據。這樣我們就引用矢量正交分解法方便地對多組數據進行計算,然后根據計算結果對中心進行調整。其方法就是將機組中心各測點數據看成一個矢量,它們分布在同一個平面上,擁有共同的中心,我們可將其看做坐標系中心(0,0),然后對各測點矢量ri在正交坐標軸線X和Y上進行正交分解(如圖1),再分別將各坐標軸上對應的分解矢量進行疊加。由于是進行中心調整,需要將疊加量除上一個n/2,得到一個新的坐標系,其圓心定為(X0,Y0),這個圓心就是機組的最佳中心,X0和Y0合矢量就是將要進行調整的中心量。最后計算出ri在新坐標系(X0,Y0)中的值ri′,將各ri′的值進行疊加取平均值,就得到圖1中的圓即為最佳中心圓。所以最佳中心就是測量圓周各測點平均半徑的中心,它與原測量圓周的中心存在一個位置偏差(X0,Y0)。根據圖1中的矢量正交分解進行矢量運算,推出最佳中心公式:
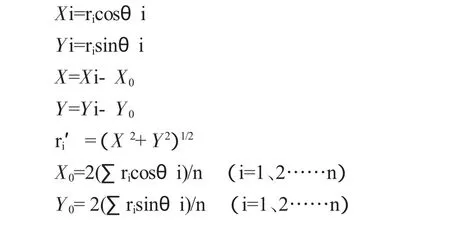
最佳中心計算法在二灘、三峽等大型水電機組安裝中已進行過成功運用。將其計算方法代入excel表格中進行公式運算,能快捷、簡便、精確地進行數據計算和分析。
2 燈泡貫流式機組發電機推力軸承加調整墊計算的運用
在燈泡貫流式機組中(如圖2),主軸由發電機導軸承(B1)和水輪機導軸承(B2)支撐,由于發電機轉子的重量(W1)和水輪機轉輪的重量(W2)橫擔在 B1、B2支撐點兩邊,則主軸會有一定的彎曲。為使發電機導軸承和主軸的接觸面以及正反向推力軸承和鏡板的接觸面均勻接觸,則須調整導軸承座與主軸的傾斜角一致,即在導軸承座后加調整墊片。在加調整墊過程中,需要測量的數據多,測量數據要求精確,所以工作量很大。為節省工作量,可利用最佳中心公式法計算求出各點數據。
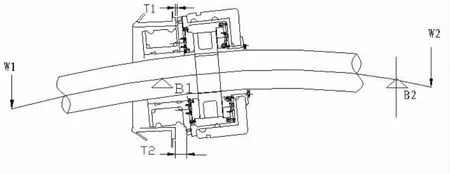
圖2 燈泡貫流式機組主軸承重支撐示圖
首先在推力軸承座加墊均布位置測量8點數據,同時將某個點定為起始點。由于測量的是軸承座與鏡板端面間的間距,可將間距值看成擁有共同中心(鏡板面)的對稱均勻分布的測點,然后利用最佳中心公式法計算軸承座端面本身的不平度。
例:某個電站軸承座與鏡板間距內徑千分尺表頭讀書為下表1,起始點角度為67.5°,點以順時針為序,將各測點數據錄入excel表格中進行公式運算結果見表1:
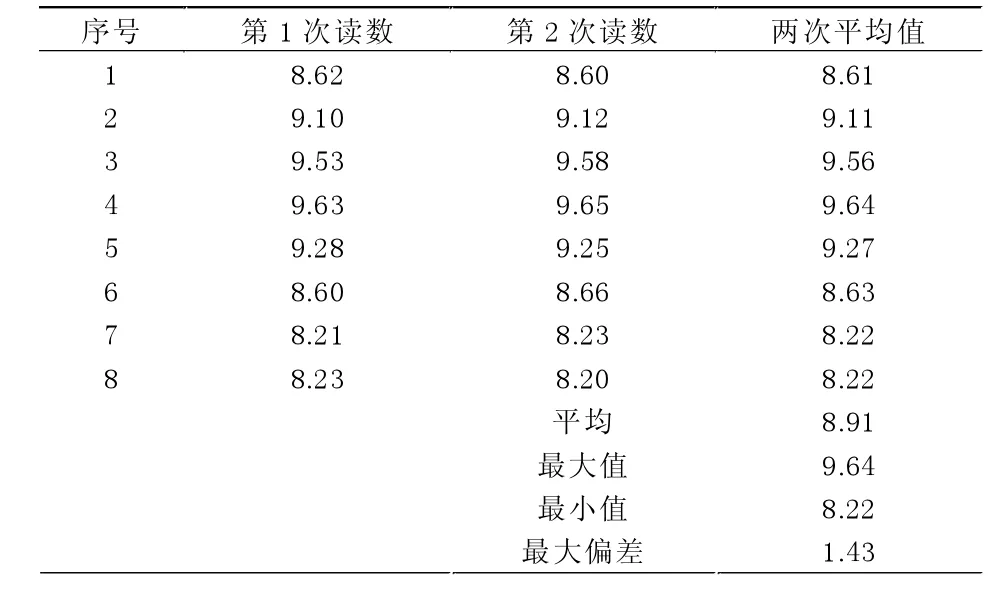
表1 未加墊測量值 單位:mm
從表1中兩次均值可看出偏差很大,現將其進行矢量正交分解,利用最佳中心法在excel表格中對其進行公式運算,計算結果如表2。表2的結果虛擬了在這8個測點位置進行了加墊,計算出軸承座端面本身不平度為0.08mm,如在實際加墊時對加墊值進行適當的增減,緊固后其端面會有微量的彈性變形,則不平度將會變小。

表2 計算加墊后各測點數據 單位:mm
從表2中得到計算平均值為8.92mm,可近似地將ri′看成一個半徑為8.92mm的圓,現在需要求出在原坐標系(0,0)中各點的ri數值,點數為48個,1號測點位置不變,則可根據矢量坐標系列 方 程 式 為 (Ricosθi-X0)2+(Risinθi-Y0)2=R02。 R0為8.92,每個點在坐標系中(0,0)對應有角度,將R0、θi、X0、Y0數值代入公式,在 excel表格中進行公式運算,求出Ri的一個正根即為各點計算數值,其數據結果見表3。由于將間距假定為一個標準圓,所以計算出的Ri中對應原測點8點數據有細微的偏差,需要進行修正,盡量保證原始值。按照此加墊完成后理論間距表頭讀書應為8.18mm,設計要求此間距最大偏差為0.06mm,實際加墊完成后測量間距最大偏差為0.04mm,滿足設計要求(計算加墊值以最小間距處進行計算,公式為δ2=δ0-11.00;δ1=Ri′-8.18-δ2)。
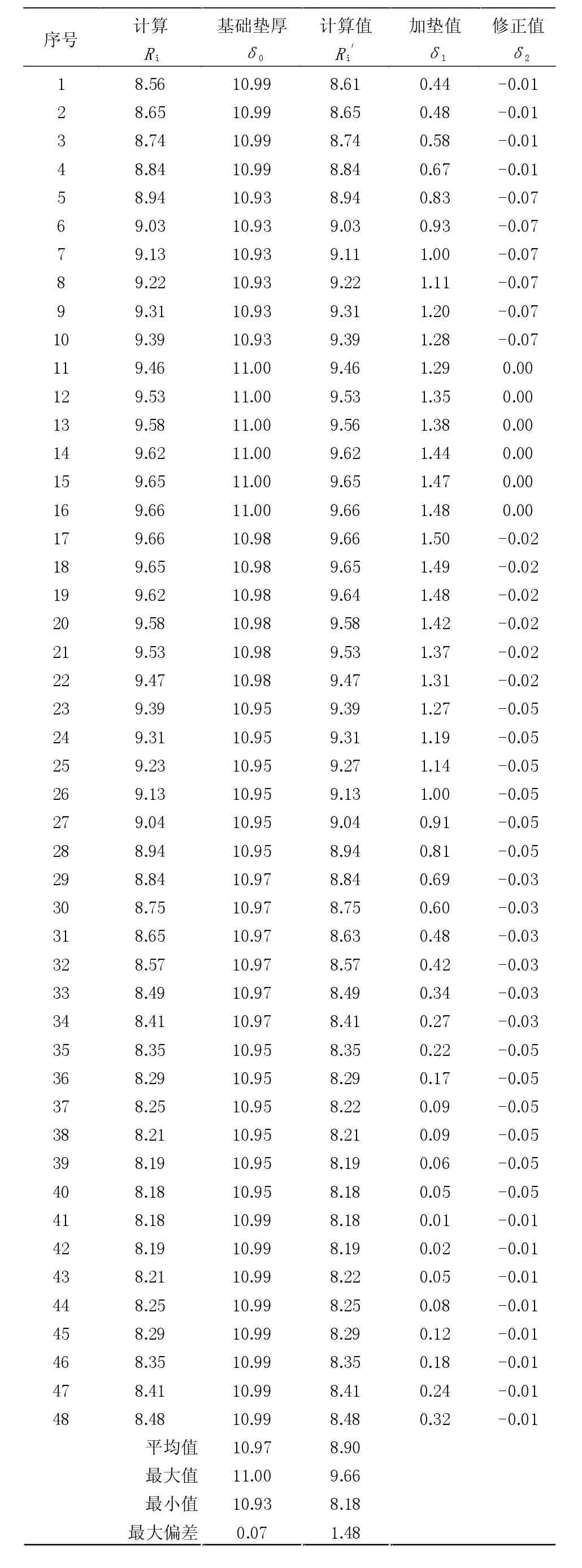
表3 計算值及其加墊值 單位:mm
3 機組軸線擺度軌跡的運用
在機組運行過程中,每道軸承處均安裝有擺度測量裝置,機組每旋轉一周,測擺探頭將測量出圓周各點擺度值,振擺分析儀將記錄下這些值。如將機組靜止時假定為0位,利用矢量正交分解法將各測點數據進行矢量分解,則可得到各點在每個軸線位置的矢量坐標,將各坐標點連接后就是機組軸心軌跡線。下表為某機組在某時刻某周期內8個均勻位置點的測量值以及根據這些測量值利用矢量正交分解法計算的坐標量和偏移中心量。

表4 機組軸心擺度分解坐標量及偏心單位:mm
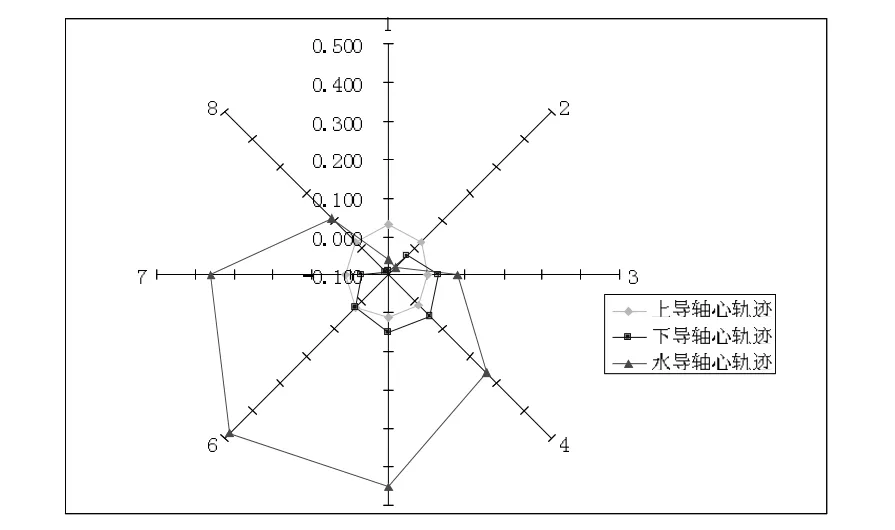
圖3 機組軸心擺度軌跡
4 結束語
在機電設備安裝中,很多地方均可運用矢量正交分解法進行計算,不僅方便,而且快捷、準確、直觀,如機組軸線調整、機組大型部件圓度、不平度計算等。本文僅在此做拋磚引玉,供讀者朋友參考及借鑒,以便能在更廣泛的領域進行研究運用。
Application of orthogonal decomposition method of vector in engineering calculation
HE Nian-min
(Sichuan Chuantou Energy Tianwanhe development Co., Ltd power plant,Shimian 625400, China)
Applies vector definition in engineering calculation, infers the optimum unit center method, then extends the method to other aspects such as the calculation of thrust bearing padding and axle centre throw orbit.
vector definition; optimum center method; thrust bearing padding calculation; axle centre throw orbit
TB113
A
1672-5387(2011)06-0067-03
2011-09-06
何念民(1974-),男,工程師,從事水電站水輪發電機組及輔助設備安裝、調試、維護與檢修等技術工作。

